
9562
.pdf
Тогда
Ввиду симметрии сечения у = 2b = 4 см. Через найденный центр тяжести прово-
дим главные центральные оси хс и ус.
2. Вычислим главные моменты инерции.
Ввиду совпадения осей хс и хс1, хс2, хс3:
Для вычисления момента инерции относительно оси ус используем формулу из-
менения момента инерции при параллельном переносе осей:
Здесь через l1, l2, l3 обозначены: соответственно расстояния между осью ус и ося-
ми ус1, ус2, ус3.
3. Нахождение наибольших напряжений и допускаемых нагрузок.
Подставляя в формулу вычисленные значения моментов инерции, а также коор-
динаты точки приложения нагрузки и точек, где возникают наибольшие растягиваю-
щие и сжимающие напряжения, получим:
В точке А(-4,136; 4) - напряжение сжатия
Из условия прочности при сжатии
множитель 104 здесь переводит квадратные, сантиметры в метры. Допускаемая нагрузка
В точке D (3,864;-2) возникает максимальное напряжение растяжения

Из условия прочности при растяжении
Допускаемая нагрузка
Выбирая меньшую из двух нагрузок, окончательно принимаем
В ходе решения этой задачи можно также порекомендовать построение ней-
тральной оси в случаях, когда трудно сразу определить координаты опасных точек. Для определения положения опасных точек в сечении следует параллельно нейтральной оси провести линии, касающиеся контура сечения. Таким образом, будут найдены точ-
ки сечения, расположенные по oбe стороны от нейтральной оси и наиболее удаленные от нeё, которые и являются опасными.
Лекция №13
Условия прочности
Для сечения произвольной формы
- для сечений типа прямоугольник, двутавр, швеллер
Перемещения и расчет на жесткость
При плоском косом изгибе линия результирующего прогиба перпендикулярна к нейтральной линии.
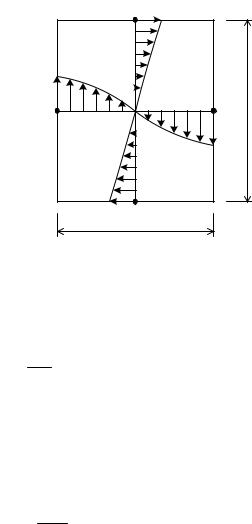
Условие жесткости
fmax ≤ [f].
Общий случай сложного сопротивления
Напомним, как распределяются касательные напряжения в поперечном сечении стержня прямоугольной формы при кручении.
Большая сторона сечения - h. Меньшая сторона сечения – b.
Наибольшее напряжение развивается в середине длинной стороны. Его определяют по формуле:
τ1 = Mкр , где Wк = β b3 .
Wк
Через τ1 выражается напряжение в середине короткой стороны: τ 2 = γ τ1 .
Угол закручивания определяется по формуле:
ϕ = Мкр l , где Jк = α b4 . G Jк
Входящие в эти формулы коэффициенты α ,β ,γ зависят от соотношения сторон прямоугольника.
Значения коэффициентов приведены в таблице.
h/b |
1 |
1,5 |
2 |
3 |
4 |
6 |
8 |
|
|
|
|
|
|
|
|
α |
0,140 |
0,294 |
0,457 |
0,790 |
1,123 |
1,789 |
2,456 |
|
|
|
|
|
|
|
|

β |
0,208 |
0,346 |
0,493 |
0,801 |
1,150 |
1,789 |
2,456 |
|
|
|
|
|
|
|
|
γ |
1,00 |
0,859 |
0,795 |
0,753 |
0,745 |
0,743 |
0,742 |
|
|
|
|
|
|
|
|
ПРИМЕР 1.
Расчётная схема консоли.
 у
у
15 Fx3 см
х
15 F
l = 1,2 м
Эп. N
+ |
15 F |
Эп. Mу
Fx45 см
у |
6 F-4 F |
|
|
|
х |
|
6 Fх3 см+4 Fх3 см |
х240 см |
Эп. Mх |
|
|
F |
|
|
Эп. Mкр |
|
Fх30 см |
Опасное сечение – жёсткая заделка:
N = 15F, Mx = F·240 см, Му = F·45 см, Мкр = F·30
см.
Формулы напряжений:
σN = |
N |
, σМ = |
М |
х |
у, |
σМ = |
Му |
х, |
τкр = |
Мкр |
. |
А |
|
|
Jу |
Wк |
|||||||
|
х |
Jх |
у |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Эпюры напряжений:
Опасная точка 1.
σz |
= |
N |
+ |
М |
х |
+ |
Му |
= |
15 F |
+ |
F ×240 |
|
+ |
|
F ×45 |
|
= (0,139 |
+ 0,741 + 0,417 ) F = 1,297 F . |
τк = 0 . |
|
|
|
|
Wу |
|
|
|
|
18 ×62 |
|
|||||||||||
|
|
А Wх |
|
|
6 ×18 6 ×182 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
|
Условие прочности: σz £ [σ ], 1,297 F = 16 кН/см2 , |
F £ 12,3 кН . |
||||||||||
|
|
Опасная точка 2. |
|
|
|
|
|||||
σ z = |
N |
+ |
|
Му |
= |
( 0 ,139 + 0,417 ) F = |
0,556 F . |
|
|
||
А |
Wу |
|
|
||||||||
|
|
|
|
|
|
|
|
||||
h / b = 18 / 6 = 3 . |
β = 0 ,801 , γ = 0,753 . |
τк = |
F × 30 |
|
= 0 ,173 F . |
||||||
0 ,801 ×6 |
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|||

Условие прочности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
£ [σ ], |
|
|
|
|
|
|
|
|
|
|
|
||
σэквIV = |
|
|
|
σz2 |
+ 3τк2 |
σэквIV = |
|
0,5562 + 3 × 0,1732 F |
0 |
,632 F |
= 16 кН/см2 , |
F £ 25,3 кН . |
|||||||||||
|
|
|
Опасная точка 3. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
σz = |
N |
+ |
Мх |
= |
(0,139 + 0,741 ) F = 0,88 F . |
τк |
= 0 |
,753 |
|
F × 30 |
= |
0,13 F . |
|||||||||||
|
Wх |
|
|
|
|||||||||||||||||||
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,801 ×63 |
|
|
|
|||||
Условие прочности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
£ [σ ], |
|
|
|
|
|
|
||||||||||||||
σэквIV = |
|
σz2 + 3τк2 |
σэквIV = |
0,882 + 3 × 0,132 F |
|
0,908 F = 16 кН/см2 , |
F £ 17,6 кН . |
||||||||||||||||
Ответ: F ≤ 12,3 кН.

|
|
|
ПРИМЕР 2. |
у |
|
F2 = 60 кН |
|
|
|
|
F1 = 800 кН |
|
|
0 |
см |
|
|
|
|
|
х |
1 |
|
|
|
|
|
соли. |
|
|
|
прочности. |
F |
20 см |
|
|
|
|
F1 = 800 кН |
|
|
F3 = 100 кН |
|
50 см |
50 см |
Проверить прочность кон-
Использовать III теорию
[ s ] = 160 МПа.
Расчётная схема консоли.
Опасное сечение – жёсткая заделка:
у |
N = 1600 кН, Му = 2000 кН см, Мкр = 1600 |
1600 кНм |
кНсм. х
40 |
|
1600 кН |
Формулы напряжений: |
|
|
|
||||||
кН |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
0,5 м |
0,5 м |
σ N = |
N |
|
σ м |
|
|
Му |
х , τ к = |
Мкр |
|
|
|
|
|
, |
|
= |
. |
||||||
|
|
|
|
|||||||||
|
Эп. N |
А |
у |
Jу |
Wк |
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
+1600
Эп. Mу |
Эпюры напряжений: |
0 0 0 2
у 
Эп. Mкр
1600
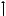 х
х
1 |
1 |
1 |
Эп. к Эп.  Эп.
Эп.  y
y
|
|
|
Опасная точка 1. |
|
|
|
|
|
|
|
|
||||||
σ z |
= |
N |
+ |
Му |
= |
|
1600 |
+ |
|
2000 |
|
= |
8,0 + 6,0 |
= 14,0 кН / см2 |
= 140 МПа. |
||
|
|
10 × 20 |
|
20 ×102 |
|
||||||||||||
|
|
А |
Wу |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
h / b = 20 / 10 = 2 . |
|
β = 0,493 , γ = |
0,795. |
τ к = |
|
1600 |
= |
3,25 кН / см2 = 32,5 МПа. |
|||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,493 ×103 |
|
|
||
Условие прочности:
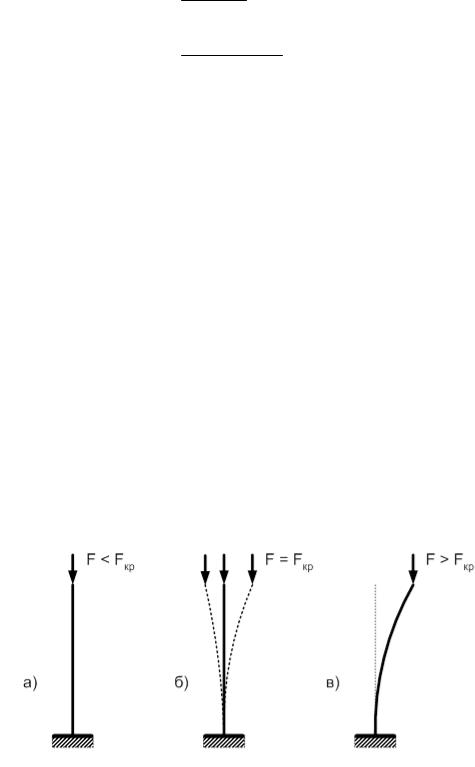
σ эквIII = 
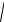 σ z2 + 4τ к2 £ [σ ]
σ z2 + 4τ к2 £ [σ ]
σ эквIII = 
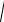 1402 + 4 × 32,52 = 154,4 МПа < [σ ] = 160 МПа.
1402 + 4 × 32,52 = 154,4 МПа < [σ ] = 160 МПа.
Таким образом, прочность консоли обеспечена.
Лекция №14
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ. ПРОДОЛЬНЫЙ ИЗГИБ.
Понятие об устойчивости первоначальной формы равновесия.
Несущая способность сжатого стержня может оказаться исчерпанной вследствие
потери устойчивости, т.е. в результате выпучивания. Выпучивание происходит рань-
ше, чем стержень выйдет из строя непосредственно от сжатия.
Известно, что равновесие абсолютно твёрдого тела бывает устойчивым, без-
различным и неустойчивым. Также обстоит дело и в механике деформируемых тел, од-
нако, для тел деформируемых вид равновесия зависит от величины прикладываемой нагрузки.
Рассмотрим длинную стойку, на которую действует осевая сжимающая сила. В за-
висимости от величины сжимающей силы можно выделить три случая поведения стой-
ки.
Рис. 71
1 случай (рис. 71а). Сжимающая сила F имеет значение меньше некоторой вели-
чины, которую называют критическая сила Fкр. Стойка находится в состоянии ус-

тойчивого равновесия, поскольку, получив малое отклонение от вертикали после «воз-
мущающего толчка», она возвращается в исходное, прямолинейное положение.
2 случай (рис.71б). Сжимающая сила равна критическому значению для данной стойки. Стойка находится в состоянии безразличного (нейтрального) равновесия: при отклонении от вертикального положения стойка приобретает равновесие и в отклонён-
ном положении. Происходит разветвление, раздвоение (бифуркация) форм равновесия. 3 случай (рис.71в). Сжимающая сила превышает критическое значение. Прямоли-
нейное состояние стойки становится неустойчивым и, при «возмущающем» толчке, она перейдёт в новое изогнутое состояние равновесия. Однако, такое состояние неприем-
лемо практически, поскольку стойка будет работать не на сжатие, а на сжатие с изги-
бом. В стойке возникнут большие нормальные напряжения, которые могут превысить предел прочности материала стойки и, следовательно, к её разрушению.
На основе рассмотренного примера можно сделать следующие выводы:
критическое состояние является предельным состоянием сжатого стержня; Оно определяется из условия устойчивости первоначального равновесного положе-
ния сжатого стержня.
изгиб, связанный с потерей устойчивости сжатого стержня, называется про-
дольным изгибом, так как его вызывает продольная нагрузка;
наибольшая сжимающая сила, при которой сохраняется устойчивость прямо-
линейной формы равновесия стержня, т.е. невозможен продольный изгиб, назы-
вается критической силой Fкр.
1. Упругий продольный изгиб. Формула Эйлера для критической силы.
Рассмотрим сжатие стержня с шарнирно закреплёнными кон-
цами критической силой Fкр (рис.72). Полагаем, что деформации стержня упругие, выполняется закон Гука, а нормальные напряже-
ния не превышают предел пропорциональности σпц.
Стержень находится в состоянии нейтрального равновесия.
Пусть стержень находится в несколько изогнутом состоянии. Изо-
гнутую ось стержня можно описать дифференциальным уравнением изогнутой оси балки:
v′′(z) = −M(z) / EJ.
Изгибающий момент в произвольном поперечном сечении M = Fкр·v. Тогда
дифференциальное уравнение примет следующий вид
v′′ + k2 v = 0, |
где k2 = F / EJ. |
|
кр |
Полученное уравнение однородное с постоянными коэффициентами. Как известно из математики, его решение имеет вид
v = C1 sin kz + C2 coskz.
Постоянные интегрирования определяем из условий закрепления стержня:
1). |
z = 0, |
v(0) = 0. |
Из этого условия следует, что С2 = 0. |
2). |
z = l, |
v(l) = 0. |
Из этого условия следует, что C1 sin kl = 0. |
Если C1 = 0, то получаем v = 0, что соответствует первоначальному, неискривлённому положению стержня. Остаётся положить, что sin kl = 0. Это равенство имеет бесчис-
ленное множество корней, т.е. kl = nπ (n = 1, 2, 3, …..).
Возведя полученное равенство в квадрат: k2l2 = n2π2 и учитывая принятое обо-
значение для k2, получим формулу критической силы сжатого стержня
F = |
n2 |
π2 EJ |
. |
|
l2 |
||
кр |
|
|
|
|
|
|
Формула подобного вида впервые выведена в 1744 г. Л. Эйлером и носит его имя.
Для инженерных расчётов необходимо знать наименьшее значение критической си-
лы, поэтому принимаем n = 1, а J = Jmin. Тогда окончательно получим
F = |
π2 |
EJ |
min |
. |
|
|
|
||
кр |
|
l2 |
|
|
|
|
|
|
Изогнутая ось стержня при продольном изгибе описывается формулой
v(z) = C1 sin πz . l
Очевидно, что изогнутая ось стержня представляет собой половину волны синусоиды.
Постоянная интегрирования С1 осталась неизвестной, поскольку стержень находится в состоянии нейтрального равновесия.
При других способах закрепления концов стержня значение критической силы может быть получено аналогично – путём решения соответствующего дифференциального уравнения изогнутой оси стержня. В простейших случаях можно ограничиться сравне-
нием формы изогнутой оси с той, которая представляет собой одну полуволну сину-
соиды. Такое сравнение позволяет записать формулы критического напряжения для случаев закрепления показанных на рис. 73.

Рис. 73
Полученные формулы можно записать в виде одной формулы, используя поня-
тие приведённой длины: lприв = µ l, где µ – коэффициент приведения, зависящий от спо-
соба закрепления концов стержня:
µ= 1 - для шарнирно закреплённого по концам стержня;
µ= 0,7 - для стержня защемлённого на одном конце и шарнирно на другом;
µ = 0,5 - для стержня защемлённого по концам;
µ = 2 - для стержня защемлённого только на одном конце.
Итак, окончательно при любом способе закрепления концов стержня формулу для критической силы можно представить в следующем виде:
F = |
π2 |
EJ |
|
|
min |
. |
|
|
|
||
кр |
(μ l)2 |
||
|
|||
2. Критическое напряжение. Неупругий продольный изгиб.
Значение нормального напряжения, вызванного в поперечном сечении стержня крити-
ческой силой, также называется критическим напряжением σкр.
Определяем критическое напряжение:
|
|
|
|
σ |
|
= |
Fкр |
= |
π2 EJ |
= |
π2 E |
, |
|
|
|
|
|
|
min |
|
|||||
|
|
кр |
A |
(μl)2 A |
(μl / i )2 |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
||||||||
где i = |
Jmin |
|
- минимальный радиус инерции поперечного сечения стержня. |
|||||||||
|
||||||||||||
min |
A |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
