
9562
.pdf
∙метод начальных параметров (универсальное уравнение изогнутой оси балки);
Метод непосредственного интегрирования дифференциального уравнения
Линейные и угловые перемещения. Основные обозначения
Расчёт балок на прочность может не удовлетворять условиям её нормальной эксплуатации из-за появления в ней значительных деформаций. Поэтому кроме расчёта на прочность необходимо проводить расчёт балки на жёсткость.
От действия внешних нагрузок, расположенных в плоскости одной из главных осей инерции поперечного сечения, балка изгибается в той же плоскости. Нейтральная продольная ось балки, прямая до деформации, переходит в плоскую кривую, которая называется изогнутой осью или упругой линией балки (рис. 48).
z |
F |
|
|
z |
|
|
z |
v(z) |
|
|
z |
Касательная к изогнутой оси балки |
l |
y |
|
Рис. 48 |
|
Сделанное ранее допущение о малости перемещений позволяет считать, что ли-
нейные перемещения – прогибы v - направлены перпендикулярно продольной оси недеформированной балки (оси z). Наибольший прогиб называется стрелой проги-
ба f.
Угловые перемещения представляют собой углы поворота θ поперечных сечений балки вокруг их нейтральных линий, или углы между направлениями продольной оси балки до и после деформирования. В упругой стадии работы материала углы поворота настолько малы, что можно считать θ ≈ tg θ. А так как согласно геометрическому смыслу производной tgθ = dv/dz, то с достаточной степенью точности угол поворота се-
чения можно принять равным первой производной от прогиба по абсциссе сечения:
θ(z) ≈ dv/dz.
Линейные и угловые перемещения сечений балки являются геометрическими характеристиками, поэтому их знак зависит от выбранной при решении задачи системы
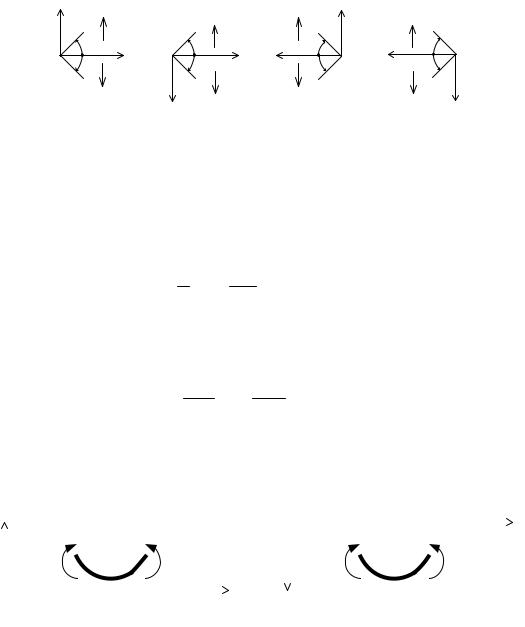
координат. На рис. 49 показаны положительные и отрицательные перемещения сечений балок для возможных систем координат.
Рис. 49
Дифференциальное уравнение изогнутой оси балки и его решение
Для определения прогибов в любом сечении балки необходимо найти аналити-
ческое выражение уравнения изогнутой оси v = v(z). Определяется оно с использовани-
ем зависимости между кривизной изогнутой оси и изгибающим моментом:
1 = M x .
ρEJ x
Сучетом малости углов поворота дифференциальное уравнение изогнутой оси
принимает упрощенный вид:
d 2v = ± M x . dz2 EJ x
Выбор знака в уравнении зависит от принятой системы координат.
|
1 |
= |
d 2v |
> 0 |
|
|
1 |
= |
d 2v |
|
|
ρ |
dz2 |
|
|
ρ |
dz2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
Рис. 50
При положительном направлении оси у вверх (рис. 50) знаки изгибающего момента и кривизны изогнутой оси балки совпадают. В этом случае в уравнении следует сохранить знак «плюс».
При положительном направлении оси у вниз (рис. 50) знаки изгибающего момента и кривизны изогнутой оси балки разные. В этом случае в уравнении следует сохранить знак «минус».
Для балки постоянного сечения уравнение удобнее записывать в виде
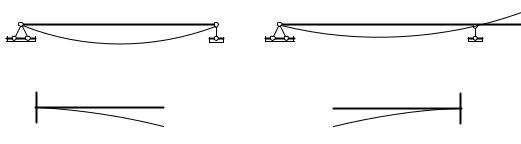
EJ x v′′( z ) = ± M x ( z ).
Перед решением полученных дифференциальных уравнений необходимо изгибающие моменты в балке Мх представить аналитической функцией от координаты z.
Интегрируя уравнение один раз получим уравнение угла поворота поперечных сечений балки:
EJ θ ( z ) = EJ |
v′( z ) |
= ± |
∫ |
M |
x |
( z ) dz + C , |
|
x |
x |
|
|
|
|
||
где С – произвольная постоянная интегрирования.
Второе интегрирование даёт уравнение прогибов балки:
где D – вторая произвольная постоянная интегрирования.
EJ x v ( z ) = ± ∫ dz∫ M x ( z ) dz + Cz + D ,
Если балка имеет n участков, то дифференциальные уравнения и необходимо со-
ставлять для каждого участка балки. Для вычисления перемещений требуется составить n выражений изгибающего момента, дважды проинтегрировать n дифференциальных уравнений и определить 2n постоянных интегрирования.
Следовательно, для определения 2n постоянных интегрирования необходимо иметь 2n условий для их нахождения, которые называются граничными условия-
ми.
Граничными условиями являются следующие условия:
Рис. 51
1) Условия закрепления балки, т.е. условия опирания балки - 2 условия (рис. 51).

2). Условие плавности изогнутой оси балки на границе участков – ( n-1) условие (рис. 52).
3). Условие непрерывности изогнутой оси на границе участков – ( n-1) условие (рис. 52).
(i-1) участок |
|
|
(i) участок |
|
|||||
|
|
||||||||
|
|
|
|
|
|
|
|
θi−1 =θi |
− условие плавности |
|
|
|
|
|
|
|
|
||
|
|
vi-1 |
|
vi |
|
||||
i-1 |
|
|
|
|
vi−1 =vi |
− условие непрерывности |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
Касательная |
|
|
i |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
к изогнутой оси балки |
|
||||||
|
|
Рис. 52 |
|
|
|
|
|
||
На границе смежных участков балки прогиб и угол поворота одинаковы как для левого, так и правого участка, т.е. перемещение, полученное из уравнения (i-1) участка,
равно перемещению, найденному из уравнения для (i) участка.
Таким образом, в сумме условия закрепления балки и условия плавности и не-
прерывности изогнутой оси на границе участков составляют 2n условий, которые по-
зволяют найти 2n постоянных интегрирования.
Метод непосредственного интегрирования дифференциального уравнения изо-
гнутой оси балки оказывается весьма трудоёмким уже при числе участков n ≥ 3, по-
скольку необходимо выполнить большой объём вычислительной работы, связанной с определением произвольных постоянных интегрирования.
Пример решения балок методом непосредственного интегрирования по участкам
Пример 1. Для заданной деревянной консоли (рис. 53) подобрать размеры прямо-
угольного сечения h и b.
Расчётные характеристики балки следующие: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ σ ] = 12 МПа, [ τ ] = 2 МПа, Е = 104 МПа. |
h = 2b |
|
|
|
|
|
|
|
Длина балки l = 1 м. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Допускаемый прогиб [ f ] = l / 200 = 1000 мм / 200 = 5 мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Определяем размеры поперечного сечения из условия прочности на изгиб. |
|||||||
|
Wx ³ |
Mx |
; |
b×4b2 |
|
³ |
1000кНсм |
= 833,3см3 |
|
|
6 |
|
|
||||
|
|
[σ] |
|
|
1,2кН /см2 |
|||
|
b = 11 см, |
h = 22 см, Jx = 11×223/12= 9760,7см4. |
||||||
2. |
Выполняем проверку балки на скалывание. |
|||||||
|
τ = |
Qy S*x |
= |
3 |
× |
Qy |
£ [τ ], τ = |
|
3×20кН |
= 0,124кН / см2 = 1,24МПа < [τ ] = 2МПа. |
|
|
|
|
|
×11×22см2 |
|||||
|
|
Jx b |
|
2 b×h |
2 |
|
||||
3. |
Определяем жёсткость балки при изгибе. |
|
||||||||
|
|
|
|
|
|
EJx = 103 × 9760,7 кНсм2 |
= 976,07 кНм2. |
|||
4. |
Определяем изгибающий момент в произвольном сечении балки. |
|||||||||
|
|
|
|
|
|
|
Мх (z) = |
-10 + 20 z –10 z 2. |
||
5. |
Составляем дифференциальное уравнение изогнутой оси и дважды его интегрируем. |
|||||||||
Ось у направляем вниз.
EJx v // = - (-10 + 20 z –10 z 2),
EJx θ = +10 z -10 z2 + 10/3 z3 + C,
EJx v = +5 z2 - 10/3 z3 + 10/12 z4 + Cz + D.
6. Условия закрепления балки.
При z = 0: θ (0) = 0. Отсюда находим С = 0, При z = 0: v(0) = 0. Отсюда находим D = 0.
7. Для углов поворота и прогибов окончательно имеем следующие выражения:
EJx θ (z) = +10 z -10 z2 + 10/3 z3.
EJx v(z) = +5 z2 - 10/3 z3 + 10/12 z4.
8. Вычисляем углы поворота и прогибы в сечениях балки (рис. 54).
Z(М) |
(РАД.) |
V(ММ) |
|
|
|
0 |
0 |
0 |
|
|
|
0,2 |
0,00167 |
0,1789 |
|
|
|
0,4 |
0,00268 |
0,6229 |
|
|
|
0,6 |
0,0032 |
1,2171 |
|
|
|
0,8 |
0,00339 |
1,8796 |
|
|
|
1 |
0,00342 |
2,5613 |
|
|
|
9. Условие жёсткости балки: мaxv = f = 2,56 мм < [ f ] = 5 мм.
Таким образом, прочность и жёсткость балки обеспечены при b = 11 см, h = 22 см.
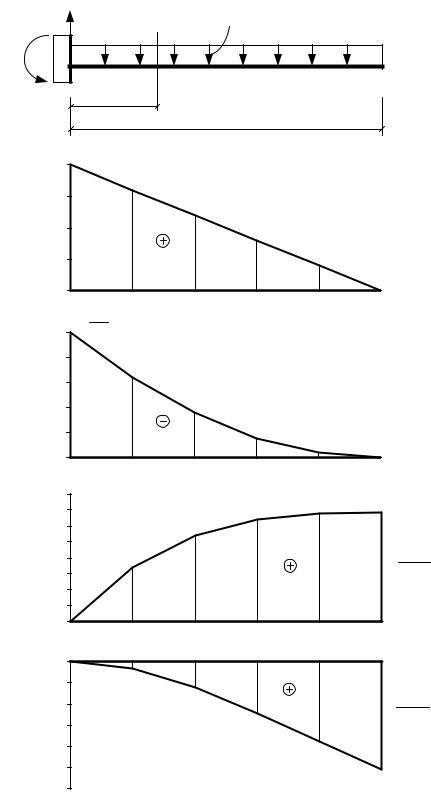
q l |
q l 2 |
2 |
q l3
6 E J
q l 4
8 E J
Рис. 54
Поэтому расчет прочности растянутого или сжатого бруса производится по нормаль-
ным напряжениям в его поперечных сечениях.

Из формулы следует, что касательные напряжения имеют наибольшие и наименьшие
значения при α = ±45º:
τ |
|
= τ |
|
= ± |
σ |
. |
O |
max |
|
||||
α=±45 |
|
|
2 |
|
||
|
|
|
min |
|
||
Площадки, на которых действуют максимальные и минимальные касательные напря-
жения τmax , называются площадками сдвига.
min
|
а) |
|
|
б) |
в) |
|
г) |
|
pα |
|
|
|
|
|
|
|
|
σα |
|
|
|
|
|
|
σ = N |
N=F |
|
τα |
|
|
|
|
N |
|
|
pα |
|
||
|
|
|
|
A |
|
|
|
||
A α |
|
n1 |
|
|
|
|
n1 |
|
α |
n |
|
n2 |
|
|
σ1 |
|
|
|
|
|
n |
|
n |
n |
|
|
|||
|
α |
|
|
n2 |
|
2 |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1 |
|
|
|
|
|
F |
|
|
F |
|
|
F |
|
|
Контрольные вопросы по теме
1.В чем заключается суть метода сечений при определении внутренних усилий, в ча-
стности, при определении продольных сил?
2.Приведите рабочее правило для определения продольных сил в поперечных сече-
ниях стержней и правило знаков для них.
3.Как определяется нормальное напряжение в поперечном сечении бруса при растя-
жении– сжатии?
4.Что такое расчетное сопротивление материала?
5.Как записываются условия прочности при растяжении-сжатии для пластичных и хрупких материалов?
6.Как производится подбор требуемой площади поперечного сечения бруса из усло-
вия прочности?
7.Как формулируется закон Гука? Как он записывается для случая растяжения– сжатия?
8.Как определяется абсолютная деформация бруса при осевом растяжении– сжатии при наличии распределенной нагрузки на грузовом участке и при ее отсутствии?
Лекция №8
Метод начальных параметров
Основные положения метода
Существует метод: метод начальных параметров, который позволяет свести ре-
шение к определению всего двух постоянных интегрирования. Для этого необходимо при решении использовать приём, который сводится к следующим правилам:
∙При решении задачи использовать единую (глобальную) систему координат для всех участков балки. Начало координат необходимо помещать на левом или правом конце балки.
∙Жесткость всех участков балки должна быть одинаковой и постоянной – EJx = const.
∙Прогиб и угол поворота в начале координат обозначим vo и θо, которые назы-
ваются геометрическими или кинематическими начальными параметрами.
∙Изгибающий момент и поперечную силу в начале координат обозначим Mo и
Qо, которые называются статическими начальными параметрами.
∙При составлении выражения изгибающего момента для нагрузки от сосредото-
ченных моментов необходимо использовать следующую форму записи: M =
M(z-a)o.
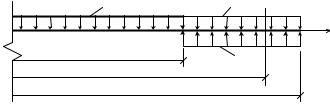
∙Если распределённая нагрузка обрывается в сечении, расположенном левее се-
чения с абсциссой z (ось z направлена вправо), необходимо нагрузку продолжить до конца балки и одновременно приложить на этой части балки такую же на-
грузку, но противоположного направления (рис. 55).
Рис. 55 |
∙При интегрировании двучленов вида (z-a)k следует пользоваться следующей формулой:
∫(z −a)k |
dz = (z −a)k+1 . |
|
k +1 |

Произвольные постоянные интегрирования на всех участках получаются одинаковыми, и решение задачи сводится к нахождению лишь двух неизвестных при любом числе участков статически определимой балки.
Универсальное уравнение прогибов и углов поворота.
Рассмотрим балку постоянного сечения, нагруженную моментом M, cосредоточенной силой F и распределёнными нагрузками (рис. 56). Ось z направим вправо. Направление нагрузок создают положительные изгибающие моменты. Рас-
сматриваемая балка имеет четыре участка, каждому из которых соответствует свое уравнение моментов, уравнение прогибов и углов поворота сечений.
Рис. 56 |
Для балки постоянного сечения дифференциальное уравнение записываем в виде
EJxv′′(z)= ±Mx (z).
Напоминаем, что в уравнении выбираем знак «плюс», если ось у направляем вверх, и знак «минус», если ось у направляем вниз. Для каждого участка балки состав-
ляем дифференциальное уравнение изогнутой оси и дважды его интегрируем.
1-й участок. 0 ≤ z ≤ а:
EJxv1′′ (z)= ±Mx(1) (z)= ±[Mo +Qo z].
EJ |
θ |
|
(z)= ± |
M z +Q |
z2 |
+ C |
. |
|
||||||||
1 |
|
|
|
|
|
|||||||||||
x |
|
|
|
o |
|
o |
2 |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
EJ v |
|
(z)= ± |
M |
z2 |
+Q |
|
z3 |
+C |
|
z + D . |
||||||
|
|
|
|
|
|
|
1 |
|||||||||
x |
1 |
|
|
o |
2 |
o |
6 |
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2-й участок. a ≤ z ≤ b:
EJxv2′′(z)= ±Mx(2) (z)= ± Mo +Qo z + M(z −a)o .
EJ θ |
|
(z)= ± |
M z +Q |
z2 |
+M(z −a) |
+C |
. |
|||||||
2 |
|
|
||||||||||||
x |
|
|
o |
|
o |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(z)= ± |
|
|
z2 |
|
|
z3 |
(z −a)2 |
|
|
|||
EJxv2 |
Mo |
|
+Qo |
|
|
+ M |
|
|
+C2 z +D2 |
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3-й участок. b ≤ z ≤ c:
EJxv3′′ (z) = ± Mx(3) (z) = ± Mo +Qo z + M (z − a)o + F (z − b) .
|
|
|
|
z2 |
|
(z − b)2 |
|
|
|||
EJxθ3 |
(z) = ± Mo |
z +Qo |
|
|
+ M(z − a) + F |
|
+ C3 . |
||||
|
|
||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
z3 |
(z − a)2 |
(z − b)3 |
|
||||
EJxv3 |
(z) = ± Mo |
|
+ Qo |
|
|
+ M |
+ F |
|
|
+ C3 z + D3 . |
|
|
|
|
|
||||||||
|
|
2 |
|
|
6 |
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4-й участок. c ≤ z ≤ l:
EJx v4′′ (z) = ± Mx( |
4 |
|
|
|
|
|
+ Qo z + M |
(z − a) |
o |
+ F (z − b) + q |
(z − c)2 |
+ tgα |
(z − c)3 |
|
||||||||
|
) (z) = ± Mo |
|
2 |
|
|
|
6 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
(z − b)2 |
(z − c)3 |
|
(z − c)4 |
|
|
|
|||||||
|
|
|
|
|
z2 |
|
|
|
|
|
||||||||||||
EJxθ4 |
(z) = ± Mo |
z + Qo |
|
|
|
+ M (z − a) + F |
|
+ q |
+ tgα |
|
|
|
+ C4 . |
|
||||||||
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
6 |
|
|
24 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
z3 |
(z − a)2 |
(z − b)3 |
(z − c)4 |
|
(z − c)5 |
|
|
|||||||||
EJx v4 |
(z) = ± Mo |
|
+ Qo |
|
|
|
+ M |
+ F |
|
|
+ q |
+ tgα |
|
|
|
+ C4 z + D4 . |
||||||
2 |
6 |
|
6 |
120 |
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
24 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изогнутая ось балки есть плавная кривая. На границах участков балки значения углов поворота и прогибов, вычисленных из уравнений соседних участков, будут рав-
ны. Эти равенства называются условиями плавности и непрерывности изогнутой оси на
границе участков.
Рассмотрим эти условия, используя полученные для балки выражения.
Граница 1-го и 2-го участков. z = a: |
θ1(a) = θ2(a). |
Отсюда следует С1 = С2. |
|
|
v1(a) = v2(a). |
Отсюда следует D1 |
= D2. |
Граница 2-го и 3-го участков. z = b: |
θ2(b) = θ3(b). |
Отсюда следует С2 = С3. |
|
|
v2(b) = v2(b). |
Отсюда следует D2 |
= D3. |
Граница 3-го и 4-го участков. z = c: |
θ3(c) = θ4(c). |
Отсюда следует С3 |
= С4. |
|
v3(c) = v4(c). |
Отсюда следует D3 = D4. |
|
Из полученного решения следует, что, используя при решении правила, изложен-
ные в пункте 2.1, постоянные интегрирования всех участков балки всегда будут равны и могут быть заменены фактически двумя постоянными интегрирования независимо от количества участков балки:
С1 = С2 = С3 = С4 = ….. = С. D1 = D2 = D3 = D4 = ….. = D.
С учётом введённых обозначений угла поворота и прогиба в начале координат из
равенств (2.3) при z = 0 получим следующие выражения постоянных интегрирования С и D:
C = EJxθo, D = EJxvo,
т.е. постоянная интегрирования С есть угол поворота в начале координат, а D – про-
гиб в начале координат, умноженные на жёсткость балки при изгибе.
