ввиду отсутствия отсеченной площади, статический момент этой площади равен нулю. С
другой стороны, если в качестве отсеченной площади рассматривать все сечение, то ста-
тический момент всей площади относительно нейтральной линии сечения z , как цен-
тральной оси, равен нулю.
Для определения касательного напряжения в точке №2 проводим через точку №2
линию, параллельную оси Oz. Отсеченная площадь лежит выше этой линии и составляет


 =2·10=20см2. Вычисляем расстояние от центра тяжести отсеченной площади до оси Oz.
=2·10=20см2. Вычисляем расстояние от центра тяжести отсеченной площади до оси Oz.
Оно равно 11см. Находим касательные напряжения в точке №2:
При определении касательного напряжения в точке №3 следует помнить, что ста-
тический момент площади отсеченной части в этом случае остается прежним, так как точ-
ки №2 и №3 находятся на одинаковом расстоянии от оси Oz. Только точка №2 принадле-
жит полке, а точка №3 принадлежит стенке двутавра. В связи с этим касательное напря-
жение в точке №3 будет равно:
Для определения напряжения в точке №4, проведем через эту точку линию, совпа-
дающую с осью Oz. Отсеченная площадь представляет собой тавр. Статический момент площади тавра вычислим, используя выражение (а), приведенное выше. В нем A1 пред-
ставляет собой площадь полки, A2 − площадь половины стенки; y1 − расстояние от центра тяжести полки до оси Oz; y2 − расстояние от центра тяжести половины площади стенки до оси Oz. Касательные напряжения в точке №4 будут равны:
Как уже отмечалось выше, в силу симметрии τ5=τ3=16,21 МПа, τ6=τ2=1,95 МПа;
τ7=τ1=0.
Откладываем найденные значения касательных напряжений от базисной линии и строим эпюру касательных напряжений.





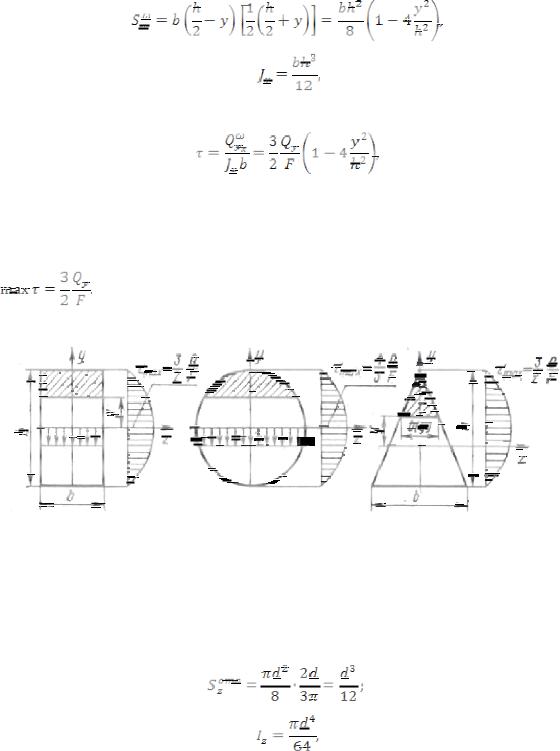
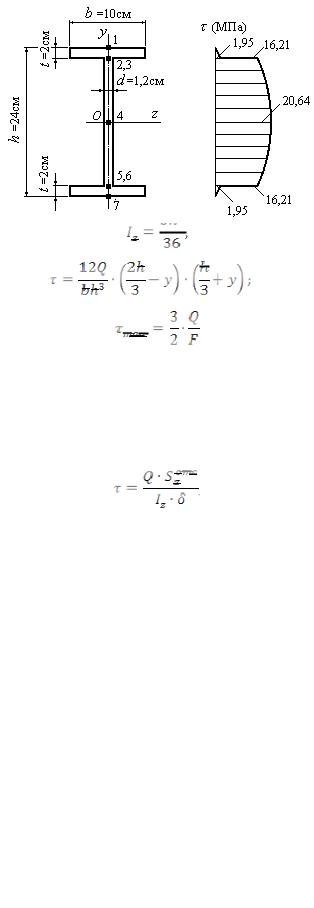







 , по которым, например, обычно проводится расчет заклепок.
, по которым, например, обычно проводится расчет заклепок.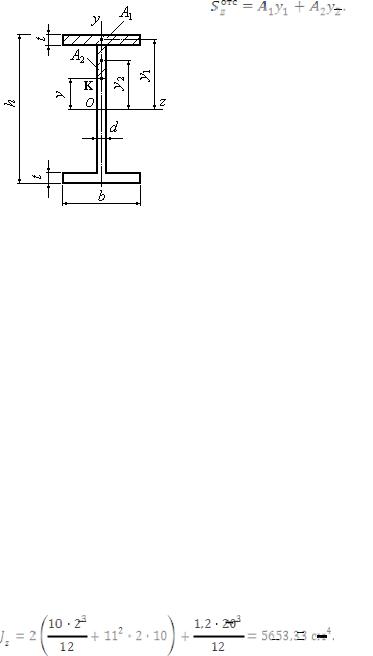





 , что будет обозначать: «значение
, что будет обозначать: «значение 

 в сечении D».
в сечении D».
 ≤ 4 м
≤ 4 м









 В силу этого на эпюре
В силу этого на эпюре 
 ≤ 7 м
≤ 7 м
 ) и
) и 
 ) заметим, что теперь справа от сечения оказа-
) заметим, что теперь справа от сечения оказа-
 м с плечом (
м с плечом (


 ) м) и часть нагрузки
) м) и часть нагрузки 


 ) с плечом (
) с плечом (


 )/2).
)/2).


































 ;
;
 ) имеет уклон в другую сторону и расположена круче, чем на 1-м и 2-м участках, поскольку тангенс угла ее наклона равен нагрузке
) имеет уклон в другую сторону и расположена круче, чем на 1-м и 2-м участках, поскольку тангенс угла ее наклона равен нагрузке 



















 =
= 









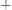


 ;
;
















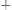





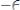



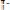

 ;
;



























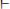


 .
.















 на некотором участке, следует сначала найти его расположение, то есть положение сече-
на некотором участке, следует сначала найти его расположение, то есть положение сече- 12 = 0,17 кН/см
12 = 0,17 кН/см

 =2·10=20см
=2·10=20см