3.4. Разностная схема Неймана-Рихтмайера - «крест» для системы уравнений газовой динамики с вязкостью.

При наличии вязкости единственным видом разрывов, допускаемых законами сохранения, является контактный разрыв. В предыдущей лекции

[см. Лекция 2] для описания течения идеального политропного газа в лагранжевых массовых переменных без учета вязкости для (n = 0) нами была определена следующая система уравнений [(3.13 а) - (3.17 а)]:

,

,

,

,

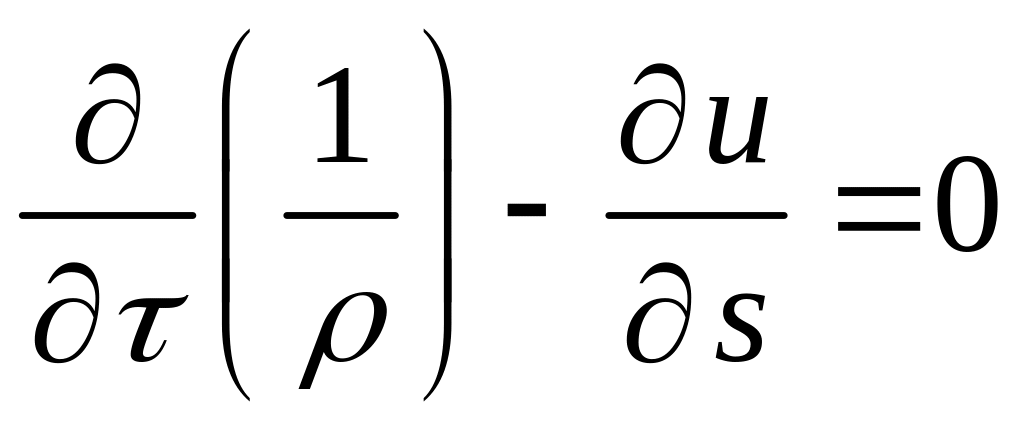Если ввести вязкость , новую переменную и заменить , то эту систему можно представить в следующем виде:

, (3.18)

, (3.19)

, (3.20)

где , , (3.21)

вязкость определяется или формулой (3.16) , или (3.17).

В случае течений без ударных волн преимущество и достоинства консервативных разностных схем становится менее очевидным. Если, однако, учесть, что ударный переход «размазывается» всего на несколько счетных интервалов, то можно понять, что это свойство остается полезным.

Первой опубликованной в печати разностной схемой, использующей «псевдовязкость», была схема Неймана-Рихтмайера. Эта схема относится к типу «крест».

Схема «крест» построена на аппроксимации первых двух законов сохранения (3.6) - (3.7) [или (3.18) - (3.19)] на прямоугольных ячейках разностной сетки в плоскости лагранжевых массовых переменных . При этом для достижения точности второго порядка и во избежание интерполяции термодинамические величины , , и скорость разнесены по разным точкам сетки – полуцелым и целым соответственно. Третье уравнение для энергии используется в недивергентном виде:

, (3.20 А)

Оно эквивалентно уравнению (3.20) и получается из системы (3.18)-(3.20) путем несложных преобразований.

Разностная схема «крест» имеет вид:

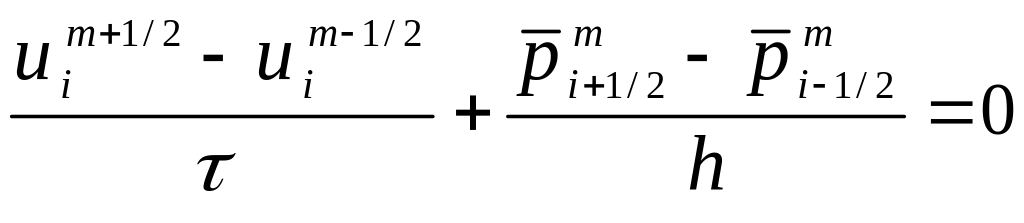, (3.22)

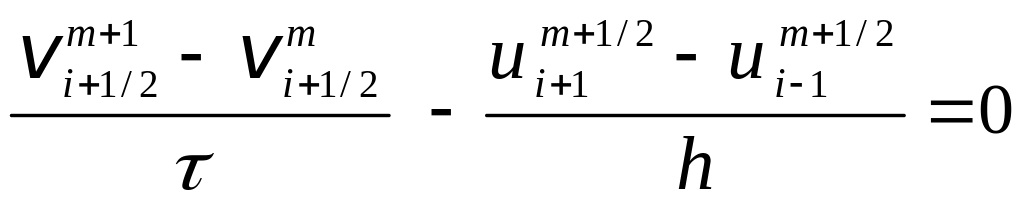, (3.23)

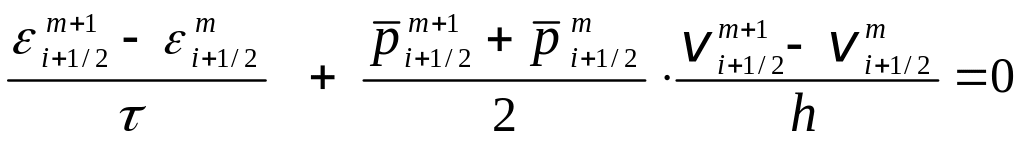, (3.24)

где , (3.25)

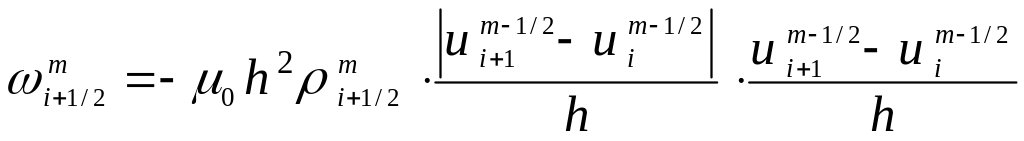, (3.26)

. (3.27)

В области гладкого течения схема имеет второй порядок точности, поскольку формулы (3.22) и (3.23) аппрксимируют законы сохранения формулой интегрирования с центрированными точками, а вязкий член имеет порядок . Формула (3.24) также имеет второй порядок точности. На Рис.2 показаны ячейки интегрирования для законов сохранения.

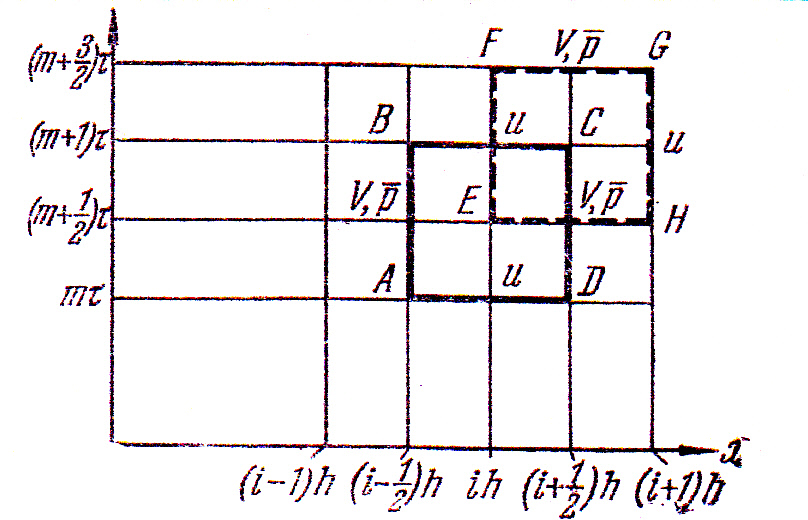
Рис.2

В практическом счете обычно избавляются от дробных шагов по времени, применяя сдвиг по временному индексу:

. (3.28)

Тогда формулы (3.22), (3.23) и (3.26) принимают вид:

, (3.29)

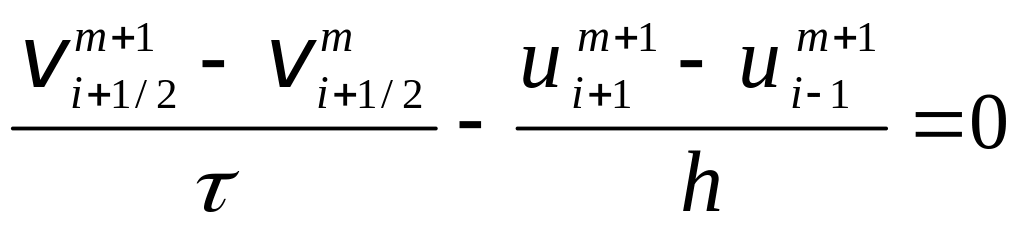, (3.30)

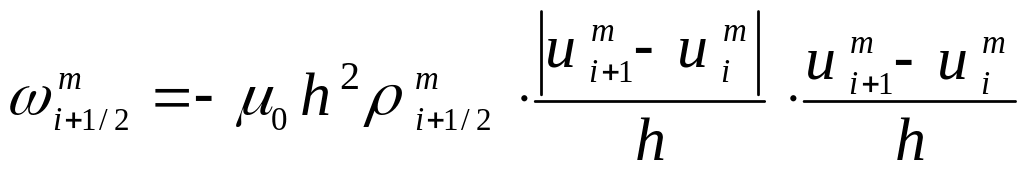. (3.31)

При произвольном уравнении состояния (3.27) формула (3.24) требует итераций для определения . В случае идеального газа формула (3.24) допускает явное разрешение относительно . Если аппроксимировать не уравнение (3.20 А)  , а закон сохранения энергии в интегральном виде (3.8), который в данном случае имеет следующий вид:

,

То при сохранении расположения точек сетки, в которых вычисляются , , и скорость , придется пользоваться интерполяцией скорости . Схемы такого рода применял И.М. Гельфанд.

Рассмотрим ряд модификаций схемы Неймана-Рихтмайера, связанные прежде всего с различным определением вязкости.

Р. Лэттер предложил модификацию метода Неймана-Рихтмайера. Вязкость вводится для того, чтобы сглаживать существующие, а также возникающие из волн сжатия ударные волны. Известно, что в волнах разрежения градиенты уменьшаются и при отсутствии вязкости. Поэтому в разностном счете целесообразно для повышения точности исключать действие вязкости в области волн разрежения, иначе говоря, «занулять» коэффициенты вязкости.

В плоском случае в волнах сжатия и ударных волнах выполняется неравенство:

,

в то время как для волн разрежения выполняется прямо противоположное условие:

.

В связи с этим Лэттер предлагает следующее выражение для вязкого члена:

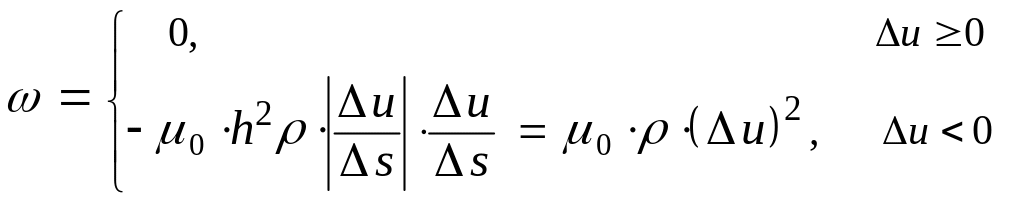(3.32)

Указанный прием становится особенно эффективным, если применять в разностном расчете линейную вязкость :

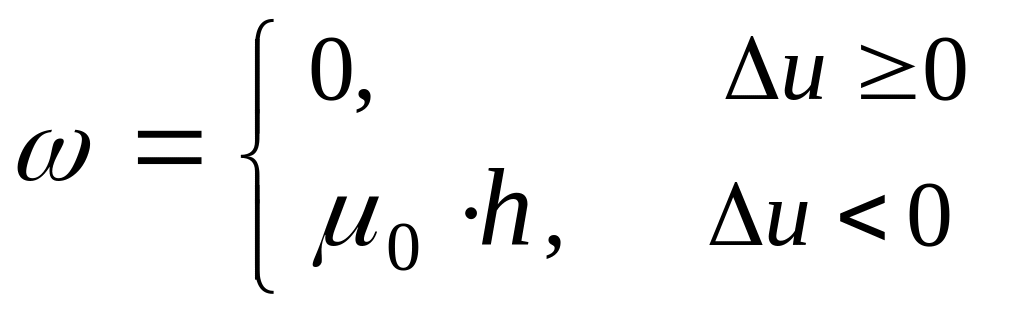
Тогда профиль ударной волны является аналитическим, осцилляционные эффекты становятся значительно меньше и при этом точность в области волн разрежения является достаточной.

Схемы (3.29) - (3.30) с условием для вязкости следующего вида:

,

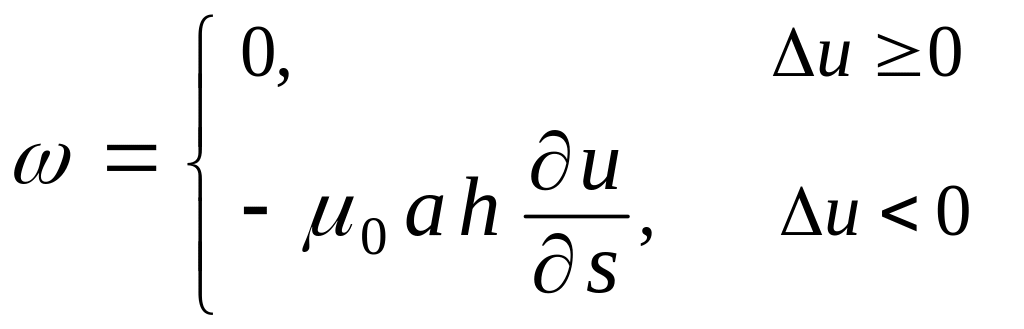где - скорость звука исследовались А.А. Самарским и В.Я. Арсениным.

Рассмотренная выше схема «крест» в версии Неймана-Рихтмайера не является консервативной разностной схемой, так как она аппроксимирует одно из уравнений (для энергии) взятое в недивергентной форме. При наличии вязкости это конечно допустимо.

Однако можно построить консервативные разностные схемы, аппроксимирующие законы сохранения вязкого газа как в лагранжевых, так и в эйлеровых координатах. Одно из преимуществ таких схем состоит в том, что они более точно передают интегральные характеристики течения при достаточно грубых сетках, чем неконсервативные схемы.

Ю.П. Попов и А.А. Самарский рассмотрели неявную разностную схему с весами, которую мы выпишем в случае лагранжевых переменных:

, (3.33)

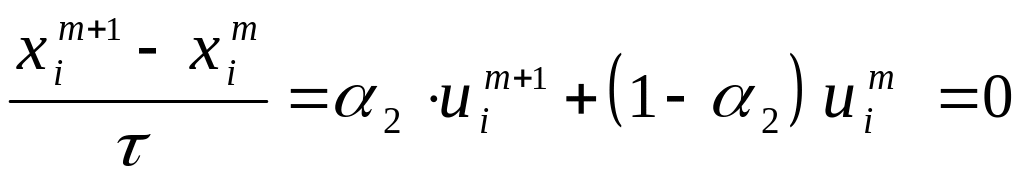, (3.34)

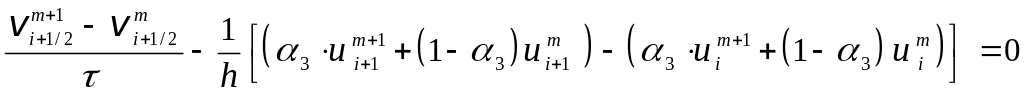, (3.35)

, (3.36)

Уравнения (3.33) и (3.34) можно рассматривать как аппроксимацию законов сохранения импульса и объема на разностной ячейке, поэтому они консервативны. Распоряжаясь параметрами , можно добиться, чтобы уравнение (3.36) в сочетании с (3.33) – (3.35) было эквивалентно аппроксимации на ячейке разностной схемы интегрального закона сохранения энергии. Это достигается при

, (3.37) где - свободный параметр. Распоряжаясь свободными параметрами, можно менять характер интерполяции по времени. При уравнение (3.36) можно преобразовать к такому виду, что оно будет иметь вид аппроксимации уравнения (3.20 А), т.е. . При выполнении этих условий авторы называют схему (3.33) - (3.36) полностью консервативной. При этом имеется ввиду, что, помимо дивергентной аппроксимации дивергентного уравнения сохранения полной энергии, схема аппроксимирует с хорошей точностью и другие (недивергентные) формы уравнения газовой динамики.

При схема (3.33) – (3.36) имеет порядок аппроксимации . Все остальные схемы этого класса имеют порядок аппроксимации . При разностная схема абсолютно устойчива (в смысле локальной устойчивости), при - схема условно устойчива.

В.Я. Гольдин, Н.И. Ионкин и Н.Н. Калиткин также повторили полную консервативную схему с аппроксимацией для уравнений в лагранжевых координатах с учетом вязкости и теплопроводности, исходя из других соображений. В.Е. Трощиев построил полностью консервативную разностную схему с аппроксимацией второго порядка, которая является явной. В случае плоской симметрии схема В.Е. Трощиева совпадает со схемой «крест» Неймана-Рихтмайера (3.22) –(3.24).

20