3.3 Однородные разностные схемы. Схемы с псевдовязкостью.

Особенностью характеристических схем и схем бегущего счета является тот факт, что регулярный и единообразный счет для них возможен

только в области гладкого течения. Наличие разрывов сильно усложняет эти методики. Поэтому возникает необходимость в единообразной схеме, формулы которой были бы однотипны в различных точках сетки независимо от наличия и характера особенностей решения в окрестности точки. Такие схемы получили название однородных.

3.3.1. Способы единообразного описания газодинамических течений.

Выше мы отметили тот факт, что если рассматривать течение сжимаемых газов и жидкостей в отсутствие вязкого трения и теплопроводности, то они описываются разрывными решениями. Это значит, что не существует систем дифференциальных уравнений, применяемых для описания разрывных течений по той простой причине, что параметры разрывных течений недифференцируемы.

Особенности, возникающие в параметрах течения следующие: слабый разрыв (разрыв производных), контактный разрыв (граница раздела между газами с различными термодинамическими параметрами) и, наконец, сильный разрыв (ударная волна).

Множество всех течений с указанными особенностями описывается единообразно на основе выполнения законов сохранения массы, импульса и энергии для любой выделенной части газа или пространства. Это приводит к выполнению интегральных законов сохранения, которые мы выпишем для случая одномерного течения с различного рода симметрией , т.е. декартовой, цилиндрической и сферической систем координат.

В эйлеровых координатах законы сохранения имеют вид:

(3.3)

(3.4)

(3.5)

В лагранжевых (массовых) координатах законы сохранения имеют вид:

(3.6)

(3.7)

(3.8)

где , а - эйлерова координата точки, заданная уравнением:

(3.9)

В этих формулах - любой кусочно-гладкий замкнутый контур и - ограниченная им область на переменных и соответственно.

Примечание. Вообще говоря, этих законов сохранения недостаточно для полного описания течения: необходимо дополнить их требованиями неубывания энтропии любой фиксированной массы газа. Это требование исключает появление неустойчивых разрывов.

Интегральные законы сохранения (3.3)-(3.5) или (3.6)-(3.8) с условием неубывания энтропии есть консервативная система уравнений газовой динамики, применимая к любым течениям, в том числе с разрывными параметрами.

Система интегральных законов сохранения чрезвычайно неудобна для разностной аппроксимации ее на фиксированной сетке в случае наличия разрывов решения, так как они требуют явного выделения линий разрыва, аппроксимации дифференциальных уравнений вне линий разрыва и удовлетворения интегральных законов сохранения на линиях разрыва (так называемые условия Гюгонио).

Замечание. Именно так описывает течение метод характеристик. Поэтому ясно, что этот метод является одним из наиболее точных методов решения интегральных законов сохранения (3.3)-(3.5) и в случае разрывных решений, если, конечно, в нем учитываются и достаточно точно все возникающие особенности решения.

Игнорирование разрывов, которые возникают в течении, и прямая аппроксимация интегральных законов сохранения на фиксированных ячейках сетки такая же, как и на гладких течениях – приводят, как правило, к неустойчивой вычислительной процедуре, в которой ударная волна заменяется колебаниями большой амплитуды.

Прямая аппроксимация интегральных законов сохранения может привести, конечно, и к устойчивому приближенному описанию параметров течения, лишь только в том случае, если возникающая при этом разностная схема вносит диссипацию - «вязкость аппроксимации». Аппроксимируя недиссипативные члены уравнений, разностная аппроксимация вносит малые, а на разрывных решениях – большие добавки, которые могут дестабилизировать или стабилизировать численное решение. Хорошая разностная аппроксимация законов сохранения должна вносить «положительную» вязкость, которую затем в расчетах стремятся минимизировать.

Устойчивыми схемами, аппроксимирующими интегральные закона сохранения без явного введения в них псевдовязкости являются схемы Лакса, Лакса-Вендроффа, С.К. Годунова.

Характерной чертой прямой аппроксимации интегральных законов сохранения является так называемое свойство консервативности или дивергентности получающихся при этом разностных схем.

Это свойство состоит в том, что уравнения разностной схемы могут быть интерпретированы как запись интегральных законов сохранения (3.3)-(3.5) или (3.6)-(3.8) для ячейки сетки, образованной пересечением прямых с прямыми при некоторой аппроксимации (или интерполяции) величин, входящих в законы сохранения на границах ячейки. Эта аппроксимация остается постоянной на данной границе ячейки, т.е. одинакова при записи законов сохранения в соседних ячейках.

Это обеспечивает свойство аддитивности консервативной разностной схемы, которое состоит в том, что при суммировании разностных уравнений по соседним ячейкам, мы получаем новое уравнение, которое также можно рассматривать как запись законов сохранения для внешней границы области, составленной из объединения этих ячеек. Короче говоря, разностные уравнения обладают теми же свойствами, что и криволинейные интегралы (3.3)-(3.5).

Это свойство дает следующее преимущество консервативным разностным схемам.

Для консервативной разностной схемы можно применить произвольные аппроксимации (интерполяции) величин на границах ячейки. Если при этом разностная схема сходится, т.е. семейство разностных решений имеет предел: (в некоторой слабой норме), то этот предел удовлетворяет именно нужным законам сохранения (3.3)-(3.5), а не каким-либо другим.

Распоряжаясь правильно имеющимся произволом в интерполяции величин на границах ячейки, можно получить дополнительные преимущества консервативных разностных схем.

Указанное свойство консервативных разностных схем схоже со свойством системы дифференциальных уравнений параболического типа:

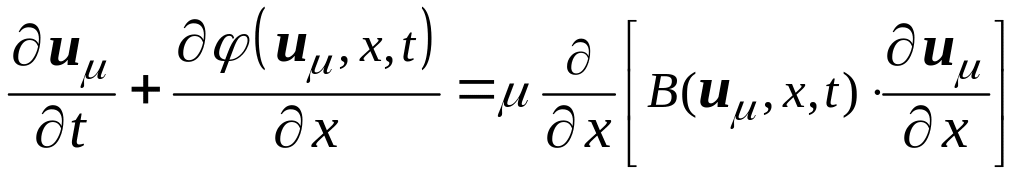, (3.10)

в которой «вязкость» - правая часть (3.10) - входит консервативным или дивергентным образом, как производная от выражения , где В –

довольно произвольная матрица.

Для системы уравнений (3.10) также имеем похожее свойство. Если при решение имеет предел , то этот предел удовлетворяет законам сохранения:

, (3.11)

То есть, является обобщенным решением системы уравнений

, (3.12)

Эта схожесть устойчивых аппроксимаций интегральных законов сохранения и «метода исчезающей вязкости» построения разрывных решений систем квазилинейных уравнений имеют не только внешний, но и глубокий характер. Для обеспечения устойчивости разностного метода в случае разрывных решений схема обязательно должна вносить «вязкость аппроксимации».

Перейдем ко второму, наиболее распространенному методу единообразного описания газодинамических течений – методу вязкости или «псевдовязкости».

В этом методе мы сразу отказываемся от детального рассмотрения ударных волн (как впрочем, и в других за исключением метода характеристик) и рассматриваем течение газов, обладающих некоторой вязкостью (и теплопроводностью), иногда, довольно похожей на настоящую физическую вязкость. В этом случае ее называют «псевдовязкостью». Вводя в уравнения газовой динамики эту искусственную вязкость, мы приближенно описываем ударные волны как плавный ударный переход.

Введение вязкости в законы газовой динамики достигается заменой давления в уравнениях (3.3)-(3.5) или (3.6)-(3.8) величиной :

, , (3.13)

где - коэффициент вязкости.

Обратим внимание, что введение вязкости повышает порядок дифференциальных уравнений по . Это требует постановки дополнительных условий на внутренних и внешних границах. На внутренних (контактных) границах это условие вытекает из требования непрерывности векторов потока импульса и энергии:

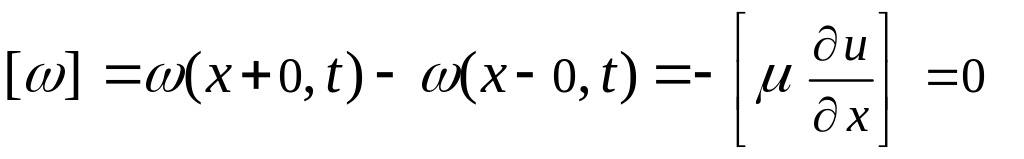. (3.14)

На внешних границах обычно ставится условие . «Физическая» вязкость (3.13) допускает контактные разрывы, она их «не размазывает». Это достоинство физической вязкости всегда стремятся сохранить, вводя другие вязкости, так называемую «псевдовязкость».

В случае постоянного коэффициента вязкости и политропного газа для эффективной ширины ударного перехода в лагранжевых переменных получается выражение:

, (3.15)

где - скачок скорости на ударной волне.

Для реальных газов коэффициент вязкости довольно мал, соответствующая реальной физической вязкости ширина ударной волны имеет порядок длины свободного пробега молекулы . Столь малая реальная вязкость недостаточна для того, чтобы можно было без проблем проводить численные расчеты, поэтому обычно полагают:

, (3.16)

где величина специальным образом подбирается так, чтобы ширина, вычисленная по формуле (3.15) для характерных условий ( - скорость звука), была приемлемой. Формула (3.16) правильно передает ширину ударной волны в разностном счете лишь при условии, что . Практически достигаются случаи .

Недостатком вязкости (3.16) является то, что она действует во всем течении, так что сильное сглаживание ударной волны, соответствующее большому значению , всегда связано с уменьшением точности расчета в областях гладкости течения.

Исходя из этих соображений, Дж. Фон Нейман и Р. Рихтмайер предложили нелинейную вязкость:

. (3.17)

Исследования показали, что ширина ударного перехода для вязкости (3.17) равна , то есть имеет порядок и не зависит от силы ударной волны. Вязкий член имеет в гладкой части течения порядок и, следовательно, не влияет сильно на точность расчета. В этом плюс формулы Неймана-Рихтмайера.

Отметим еще одну особенность вязкости Неймана-Рихтмайера. В отличие от линейной вязкости, терпит разрыв вторая производная. Так как в области ударной волны градиенты всегда велики, то этот разрыв производных приводит к постоянному источнику возмущений, вызывающих сильные осцилляции гидродинамических величин в окрестности фронта ударной волны. Его примерный вид представлен на Рис.1.

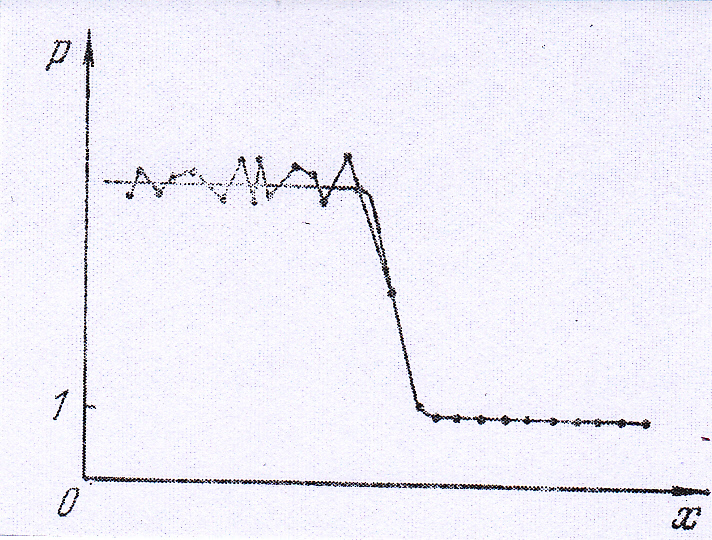
Рис.1

При этом амплитуда осцилляций возрастает при уменьшении коэффициента вязкости.

Сильная зависимость профиля разностной ударной волны от составляет характерную особенность схемы Неймана-Рихтмайера, которая в некоторых случаях затрудняет интерпретацию результатов.