7. Выделим минимальное число импликант из предыдущего шага, покрывающих минтермы. Получаем
Ответ.
f(x1,x2,x3х4)=
-минимальная дизъюнктивная нормальная
форма
Задача 8. Используя метод диаграмм Вейча, необходимо найти МДНФ функции, принимающей значение 1 на наборах: 1,3,5,7,14,15.
Решение.
Составим карту Карно для этой функции. Объединяя ячейки с единицами, получим 2 группы. Для каждой группы запишем соответствующую элементарную конъюнкцию.
|
|
x3x4 |
|||
|
|
00 |
01 |
11 |
10 |
x1x2 |
00 |
|
1 |
1 |
|
01 |
|
1 |
1 |
|
|
11 |
|
|
1 |
1 |
|
10 |
|
|
|
|
|
0--1 —>
-для
четырёх ячеек, выделенных оранжевым,
111- —>
-
для двух ячеек, выделенных жёлтым.
Ответ. f (x1
, x2 ,x3,x4)=
– минимальная дизъюнктивная нормальная
форма.
Рисунок для номеров 9-13:
Задача 9
Задать данный граф перечислением, матрицей смежности и инцидентности.
Решение:
Граф можно задать перечислением элементов множества вершин и множества ребер. Для графа, изображенного на рисунке, эти множества: V={A,B,C,D,E,F,G,M}-множество вершин и E={AB,AG,AF,BC,DC,ED,EM,EG,FE,FG,GB,GM,MC}-множество дуг.
Матрица инцидентности – это прямоугольная матрица, число строк которой равно числу вершин, количество столбцов – числу дуг (рёбер) графа. На пересечении строки и столбца ставится 1, если вершина является началом дуги, -1 – если концом дуги, 0 – если вершина и дуга не инцидентны.
-
AB
AG
AF
FE
FG
GB
GM
EG
EM
ED
DC
MC
BC
A
1
1
1
0
0
0
0
0
0
0
0
0
0
B
-1
0
0
0
0
-1
0
0
0
0
0
0
1
C
0
0
0
0
0
0
0
0
0
0
-1
-1
-1
D
0
0
0
0
0
0
0
0
0
-1
1
0
0
E
0
0
0
-1
0
0
0
1
1
1
0
0
0
F
0
0
-1
1
1
0
0
0
0
0
0
0
0
G
0
-1
0
0
-1
1
1
-1
0
0
0
0
0
M
0
0
0
0
0
0
-1
0
-1
0
0
1
0
Матрица смежности – это квадратная матрица, размер которой определяется числом вершин в графе. На пересечении строки и столбца ставится 1, если вершины инцидентны и 0 в противном случае.
-
A
B
C
D
E
F
G
M
A
0
1
0
0
0
1
1
0
B
1
0
1
0
0
0
1
0
C
0
1
0
1
0
0
0
1
D
0
0
1
0
1
0
0
0
E
0
0
0
1
0
1
0
1
F
1
0
0
0
1
0
1
0
G
1
1
0
0
1
1
0
1
M
0
0
1
0
1
0
1
0
Задача 10. 10.Определить следующие основные характеристики графа:
Число рёбер и дуг;
Число вершин;
Коэффициент связности графа (число компонент связности);
Степень всех вершин;
Цикломатическое число графа.
Решение:
Число рёбер -0, число дуг (направленных рёбер)-13, число вершин-8, число компонент связности -1.
Степенью вершины называется число инцидентных ей ребер. В случае дуг точнее говорить о полустепенях вершин. Полустепень исхода вершины A равна 3, полустепень захода вершины A равна 0, полустепень исхода вершины B-1, полустепень захода вершины B-2, полустепень исхода вершины C-0, полустепень захода вершины C-3, полустепень исхода вершины D-1, полустепень захода вершины D-1, полустепень исхода вершины E-3, полустепень захода вершины E-1,полустепень исхода вершины F-2, полустепень захода вершины F-1, полустепень исхода вершины G-2, полустепень захода вершины G-3, полустепень исхода вершины M-1, полустепень захода вершины M-2.
Цикломатическим числом или циклическим рангом графа называется наименьшее число ребер (дуг), которое необходимо удалить из графа так, чтобы в нем не осталось ни одного цикла. После такого удаления ребер из связного графа будет получено дерево, называемое остовным деревом или остовом графа. n(G)=q-p+y =13-8+1=6, где q-число дуг, p-число вершин, y - число компонент связности графа G.
Задача 11. Определить, является ли данный граф:
Планарным или плоским (обосновать ответ и выполнить обратное преобразование)
Двудольным графом (обосновать ответ и если необходимо, то достроить до двудольного)
Деревом (обосновать ответ, в случае циклического графа, привести один из вариантов остовного дерева)
Псевдографом или мультиграфом, или простым графом (обосновать ответ и выполнить необходимые преобразования)
Решение:
Планарным или плоским (обосновать ответ и выполнить обратное преобразование). Плоский, так как все пересечения его рёбер являются вершинами графа. Преобразуем этот граф в планарный.
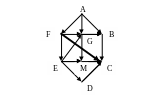
Двудольным
графом (обосновать ответ и если
необходимо, то достроить до двудольного)
Граф является двудольным, если множество
его вершин V
можно разбить на
два не пересекающихся класса V1
и V2
так, что каждое ребро
имеет одну вершину в V1,
а вторую -в V2.
Данный граф не является двудольным,
так как содержит циклы нечётной длины,
например A-G-B,
и поэтому множество его вершин нельзя
разделить на две части. Для того, чтобы
преобразовать граф в двудольный,
необходимо, например, разбить дуги AB,
AF,
EG
на две части с добавлением вершин
A1,A2,E1.
В результате данного преобразования
все циклы в графе будут иметь чётную
длину, тогда множество вершин можно
разделить на две доли (их номера стоят
после названия вершины).
Деревом (обосновать ответ, в случае циклического графа, привести один из вариантов остовного дерева) Не является деревом, например, остовным деревом может являться
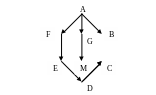
Псевдографом или мультиграфом, или простым графом (обосновать ответ и выполнить необходимые преобразования) Данный граф является простым, поскольку не содержит петли, изолированные вершины и кратные связи.
Преобразуем данный граф в мультиграф (граф с параллельными дугами):
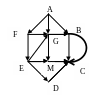
Преобразуем данный граф в псевдограф (мультиграф с петлями):
Задача 12.Определить метрические характеристики графа: диаметр, радиус, эксцентриситет каждой вершины, центральные вершины.
Решение.
Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа.
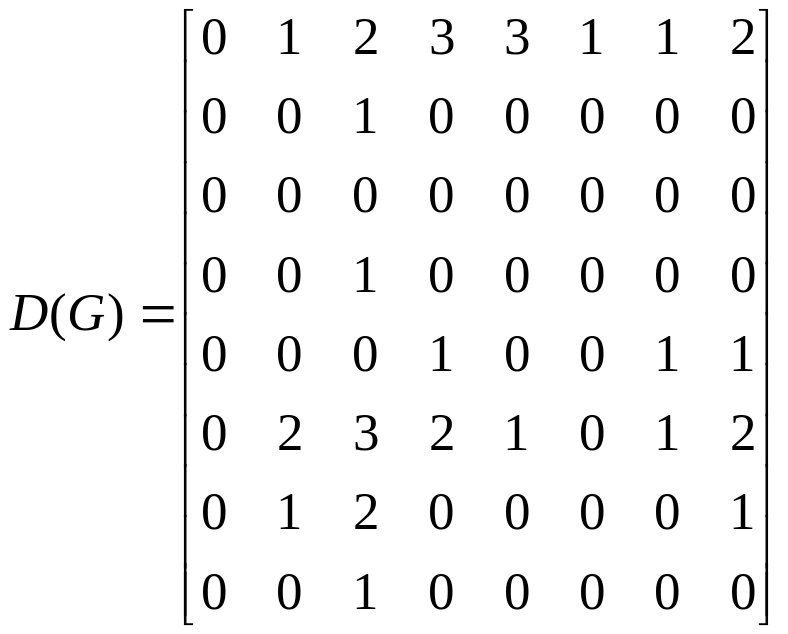
С
помощью полученной матрицы для каждой
вершины графа G
определим наибольшее расстояние из
выражения: 
для
i, j
= 1, 2, …, 8. В результате
получаем эксцентриситеты вершин: r(A)
= 3, r(B)
=1, r(C)
=0, r(D)
= 1, r(E)
=1, r(F)
= 3, r(G)
=2, r(M)
=1. Минимальное из
полученных чисел является радиусом
графа G,
максимальное – диаметром графа G.
Значит, R(G) = 0
и D(G) = 3,
центром является вершина С.