Вариант №30.

Задача 1. Для заданных множеств А, В и С найдите:

АВ, АВС, АВ, АВС, A \ B, B \ A, A \ C, C \ A, (А \ В) \ С, А \ (В \ С), А  B, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А=[-2, 4]– отрезок числовой оси

В=(–10; 0.5) – интервал на числовой оси

С=[0; 10] – отрезок числовой оси

Решение Объединением двух множеств A и B называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B, поэтому:

АВ =(-10;4 АВС = (-10; 10

Пересечением двух множеств A и B называется множество элементов, принадлежащих одновременно и A, и B, поэтому:

АВ =[-2;0,5)

ВС = 0;0.5)

АВС = 0;0.5)

Относительным дополнением множества B до множества A называется множество тех элементов A, которые не являются элементами B, поэтому

А \ В = [0,5;4]

В \ А =(–10;-2)

А \ С = [-2;0)

С \ А = (4; 10

(A \ B) \ C = 

A \ (B \ C) = [0;4]

Симметрической разностью двух множеств A и B называется объединение двух разностей A \ B и B \ A, а абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, поэтому:

AB=( А \ В)( В \ А)={(–10;-2), [0,5;4]}

ABC=((AB)\C)(C\ (AB))={(–10;-2),[0;0,5), (4;10]}

={(-;-2),(4;+)}

={(-;-10],[0,5;+)}

={(-;0),(10;+)}

Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b) таких, что и , поэтому:

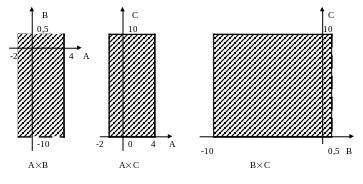
Задача 2. Даны отображения (числовые функции) ƒ и g. Найдите область определения и область значений отображений. Определите, являются ли они инъективными, сюрьективными или биективными в найденных областях. Найдите композицию (ƒ ◦ g), (g ◦ ƒ), обратные (слева и справа) отображения: ƒ^–1, g^-1, (ƒ ◦ g)^-1, (g ◦ ƒ)^-1. Для заданных множеств A, B  ℝ найдите f(A), g(A), ƒ ^–1(B), g^-1(B). Найдите также неподвижные точки отображений.

и , A = [0; 3] и B = [ ‑1; 0].

Решение: область определения отображения f – это множество таких значений х, для которых имеется вещественное число у такое, что у=f(x). И, так как для любого вещественного числа х найдется число у с указанным свойством, то пр₁f = ℝ – множество всех вещественных чисел.

Аналогично, область определения отображения g: пр₁g = ℝ.

Область значений отображения f – это множество всех образов элементов хпр₁f. Тем самым, пр₂f ={y ℝ.: y  -1 }. А область значений отображения g – это множество всех вещественных чисел, т.е. пр₂g = ℝ.

Отображение g является инъективным, поскольку для каждого упр₂g, имеется ровно один х пр₁g (или каждый образ имеет ровно один прообраз). Отображение f инъективным не является, т.к. для некоторых упр₂f, имеется более одного прообраза, например: для у=0 прообразами будут х=1 и х=3.

Отображение g является сюрьективным, поскольку для каждого упр₂g, имеется хотя бы один хпр₁g (или каждый образ имеет хотя бы один прообраз). Отображение f также является сюрьективным, т.к. для каждого упр₂f, имеется хотя бы один хпр₁f такой, что у = f(x).

Так как g одновременно инъективно и сюрьективно, то оно является биективным отображением.

Найдем композицию отображений:

(f∘g)(x) = f(g(x)) = (g(x)–2)²–1 = (1–x–2)² –1 = (–x–1)² – 1=(x+1)²–1,

(g∘f)(x) = g(f(x)) =1– f(x) = 1 – (x–2)² +1 = 2 – (x–2)².

Отображение f обратимо справа, как сюрьекция. И , где y –1. Из выражения найдем x. Тогда и , где y –1.

При этом, (f∘f ^‑1)(у) = f(f ^‑1(y))= – тождественное отображение при y  ‑1.

Отображение g обратимо как слева, так и справа, как биекция. И , где y любое. Из выражения следует: . И при этом: (g∘g^‑1 )(у) = g(g^‑1(y)) = 1 – ( 1– y ) = y и (g^‑1∘g )(х) = – тождественные отображения.

По свойствам композиции

f(A) = { y = f(x), где xA }, поэтому f(A)=[–1; 3].

Аналогично, g(A) = { y = g(x), где xA } = [–2; 1].

Найдем неподвижные точки. По определению это такие х, что: f(x)=x и g(x)=x. Таким образом, x = (x–2)²–1. Отсюда x²–5x+3=0 и т. к. дискриминант D=25–12=13>0, то – две неподвижные точки f(x).

Из g(x)=x следует, что x=1–x и – неподвижная точка g(x).

Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах:

Решение