
- •Методические рекомендации для преподавателя
- •§ 1. Простейший поток событий и его свойства
- •§ 2. Случайный процесс с дискретным числом состояний
- •§ 3. Смо с отказами
- •§ 4. Смо с ожиданием
- •§ 5. Смо с ожиданием с ограничением на длину очереди
- •§6. Смо смешанного типа с ограничением времени ожидания в очереди
§ 1. Простейший поток событий и его свойства
Под потоком событий в теории вероятностей понимается последовательность событий, происходящих одно за другим в какие-то моменты времени.
Примерами могут служить: поток вызовов на телефонной станции; поток клиентов в химчистке; поток машин, требующих ремонта, подъезжающих к мастерской и т.п.
Введем определения.
1. Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени длиной t зависит только от длины участка и не зависит от того, где на оси Оt он расположен.
2. Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
3. Поток событий называется ординарным, если вероятность попадания на достаточно малый участок t двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
Если поток событий обладает всеми тремя свойствами (т.е. стационарен, ординарен и не имеет последействия), то он называется простейшим или стационарным пуассоновским потоком.
Закон распределения длины промежутка времени между соседними событиями – показательный. Пусть Т – промежуток времени между двумя соседними событиями в простейшем потоке. Тогда функция распределения
F(t) = P(T < t) = 1 – e–t (t>0), (1.1)
где – плотность потока событий, т.е. среднее число событий, происходящих в единицу времени.
Дифференцируя (1.1), найдем дифференциальную функцию распределения (черт. 1):
f(t) = e–t (t>0). (1.2)
Ч исло
событий за время t
будет t.
исло
событий за время t
будет t.
§ 2. Случайный процесс с дискретным числом состояний
С истема
Х называется системой с дискретным
числом состояний Х1, Х2,
…, Хn, …,
если переход из одного состояния в
другое осуществляется скачком. Возможные
состояния системы изображаются с помощью
так называемого графа состояний, на
котором состояния изображены
прямоугольниками, а возможные переходы
системы из состояния в состояние –
стрелками.
истема
Х называется системой с дискретным
числом состояний Х1, Х2,
…, Хn, …,
если переход из одного состояния в
другое осуществляется скачком. Возможные
состояния системы изображаются с помощью
так называемого графа состояний, на
котором состояния изображены
прямоугольниками, а возможные переходы
системы из состояния в состояние –
стрелками.
На черт. 2 изображен граф системы, имеющей 3 состояния и возможные переходы из Х1 в Х2, из Х1 в Х3, из Х3 в Х2, из Х3 в Х1. Состояние Х2 – состояние без выхода. На черт. 3 изображен граф системы, имеющей четыре состояния.
Для описания случайного процесса, протекающего в системе, используются вероятности состояний p1(t), p2(t), …, pn(t), где pk(t) (k = 1, 2, …, n) – вероятности того, что в момент t система находится в состоянии Хk.
Вероятности pk(t) удовлетворяют условию:
![]() .
.
Пусть переходы системы из одного состояния в другое осуществляются под влиянием простейших потоков событий. В этом случае для вероятностей состояний системы p1(t), p2(t), …, pn(t) можно составить систему линейных дифференциальных уравнений. При составлении дифференциальных уравнений удобно пользоваться размеченным графом состояний, на котором у каждой стрелки, ведущей из состояния в состояние, проставлена плотность (интенсивность) потока событий, переводящего из состояния в состояние по данной стрелке (черт. 4).
З десь
i,j
обозначает плотность потока событий,
переводящего систему из состояния Хi
в состояние Хj.
десь
i,j
обозначает плотность потока событий,
переводящего систему из состояния Хi
в состояние Хj.
Если имеется размеченный граф состояний
системы Х, то систему дифференциальных
уравнений для вероятностей pk(t)
(k = 1, 2, …, n)
можно составить, пользуясь простым
правилом. В левой части каждого уравнения
стоит
![]() ,
а в правой – столько членов, сколько
стрелок связано непосредственно с
состоянием Хk.
Если стрелка ведет в данное состояние,
то член имеет знак плюс, если ведет из
данного состояния, то член имеет знак
минус. Каждый член равен плотности
потока событий, переводящего систему
по данной стрелке, умноженной на
вероятность того состояния, откуда
исходит стрелка. Например, для системы
Х с размеченным графом (черт. 4)
система дифференциальных уравнений
будет:
,
а в правой – столько членов, сколько
стрелок связано непосредственно с
состоянием Хk.
Если стрелка ведет в данное состояние,
то член имеет знак плюс, если ведет из
данного состояния, то член имеет знак
минус. Каждый член равен плотности
потока событий, переводящего систему
по данной стрелке, умноженной на
вероятность того состояния, откуда
исходит стрелка. Например, для системы
Х с размеченным графом (черт. 4)
система дифференциальных уравнений
будет:
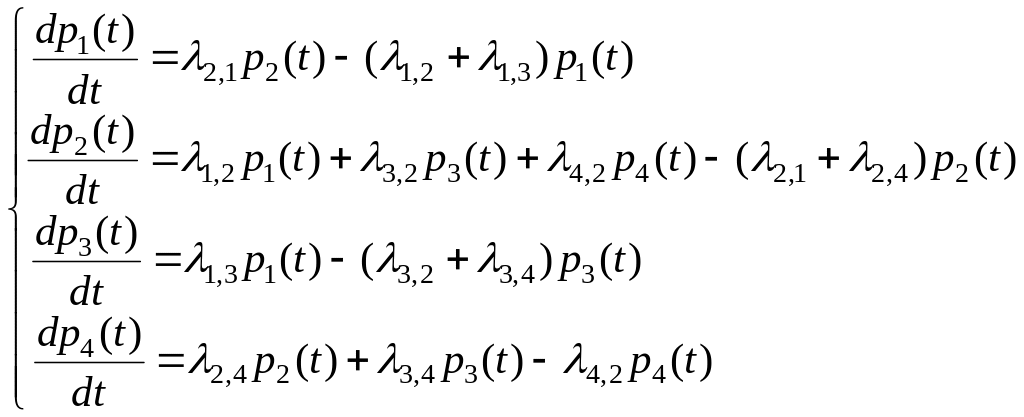
Число уравнений можно уменьшить на 1, если учесть, что p1(t) + p2(t) + p3(t) + p4(t) = 1.
Начальные условия для интегрирования такой системы отражают состояние системы в начальный момент. Если, например, при t = 0 система была в состоянии pk, то pk(0) = 1; pi(0) = 0, где i ≠ k.
Предельным режимом для системы Х
называется случайный процесс,
устанавливающийся в системе при t⇢∞.
В этом случае
![]() .
Следовательно,
.
Следовательно,
![]() .
Если число состояний системы конечно,
нет состояний без выхода, то предельный
режим существует и характеризуется
предельными вероятностями p1,
p2, …, pn
.
Если число состояний системы конечно,
нет состояний без выхода, то предельный
режим существует и характеризуется
предельными вероятностями p1,
p2, …, pn
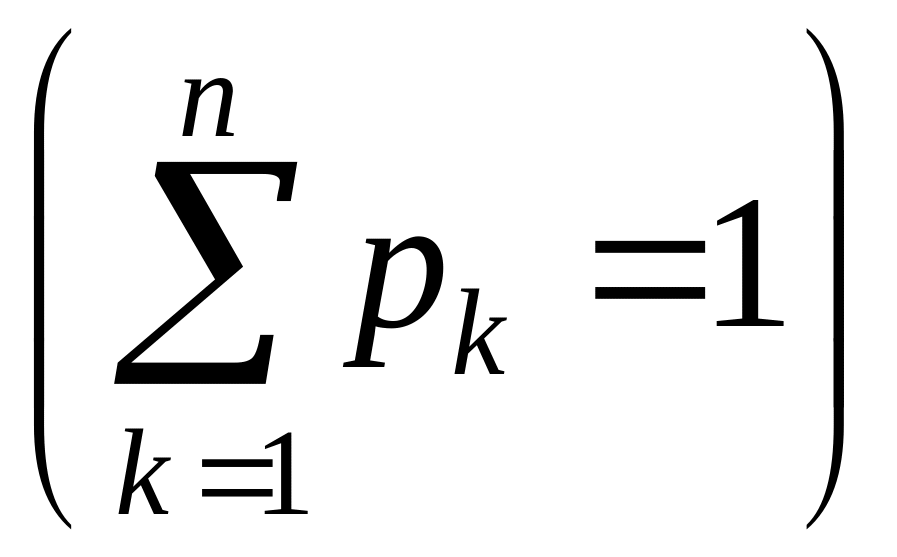 .
.
Чтобы найти pk,
приравниваем нулю левые части
дифференциальных уравнений (полагаем
![]() = 0)
и решаем полученную систему линейных
алгебраических уравнений. К ним добавляем
нормировочное условие
.
= 0)
и решаем полученную систему линейных
алгебраических уравнений. К ним добавляем
нормировочное условие
.
Для системы Х предельный режим будет определяться системой алгебраических уравнений
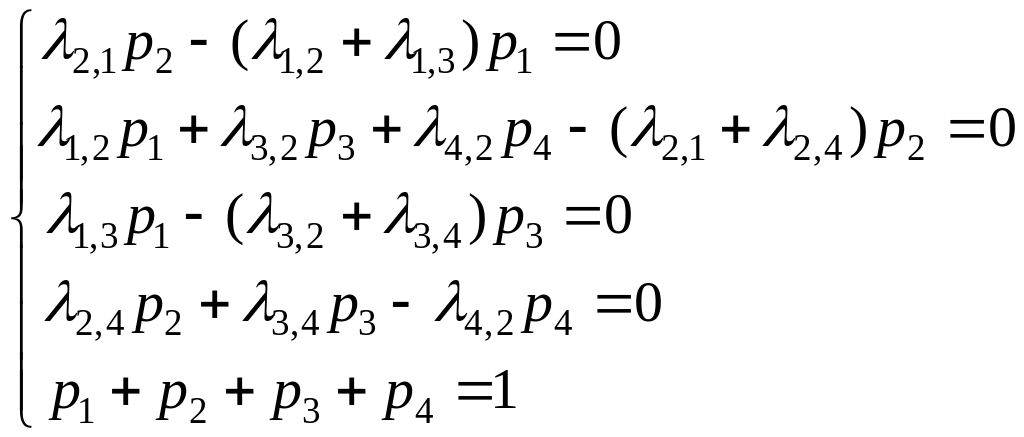
Пример. Известен граф состояний системы:
1) Составить дифференциальные уравнения
для вероятностей![]() ,
если известно, что в начальный момент
времени система находится в состоянии
,
если известно, что в начальный момент
времени система находится в состоянии
![]() .
.
2) Для стационарного режима составить
систему линейных уравнений и найти
предельные вероятности
![]() .
.
Решение.
1)
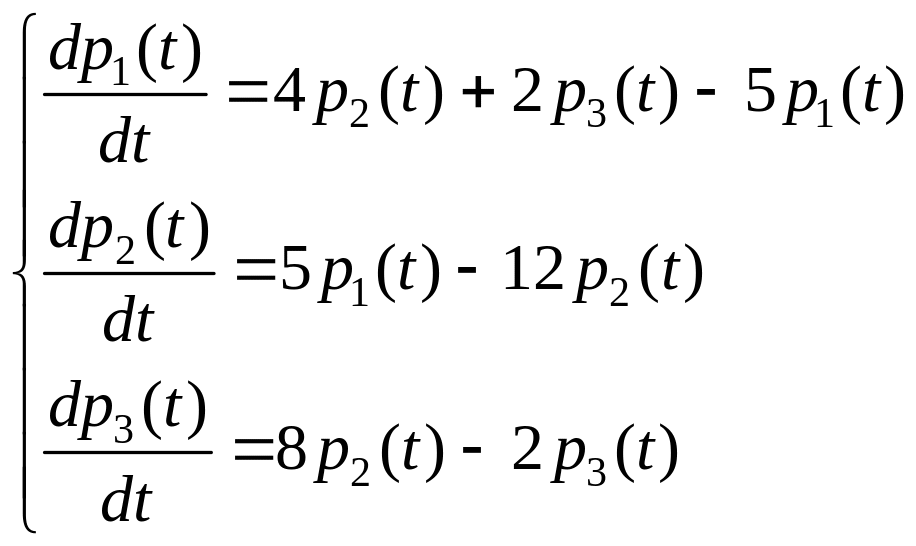
![]() .
.
Начальные условия:
![]() .
.
2) Для стационарного режима имеем:
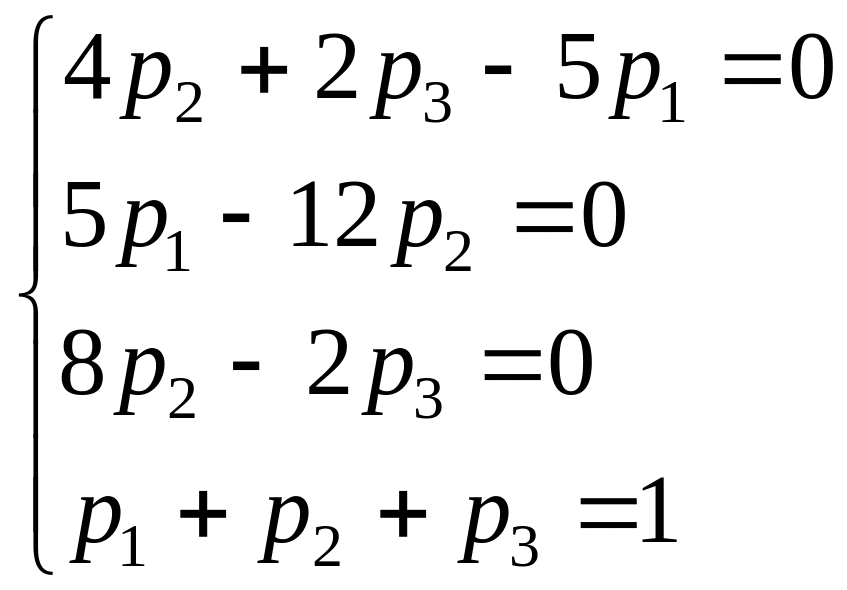
Из системы находим:![]() ,
,
![]() .
Подставим в 4-е уравнение:
.
Подставим в 4-е уравнение:
![]() ,
,
![]() ,
,
![]() .
.
Заметим, что 1-е уравнение оказалось «лишним». Но его можно использовать для проверки.
