
- •Глава 7 Производные, дифференциалы функций
- •§ 7.1. Понятие производной, ее геометрический и физический смысл
- •§ 7.2. Правила дифференцирования
- •§ 7.3. Таблица производных
- •§ 7.4. Производные неявно заданных функций
- •§ 7.5. Дифференцирование функций, заданных параметрически
- •§ 7.6. Первый дифференциал функции, инвариантность его формы
- •§ 7.7. Производные и дифференциалы высших порядков
- •§ 7.8. Формула Тейлора
Определить точки
разрыва функции
![]() ,
если они существуют, построить рисунки
,
если они существуют, построить рисунки
6.25.
![]() ,
6.26.
,
6.26.
![]() .
.
Глава 7 Производные, дифференциалы функций
§ 7.1. Понятие производной, ее геометрический и физический смысл
Определение
1. Производной (первой производной)
функции
![]() называется предел отношения приращения
функции к приращению аргумента при
стремлении приращения аргумента к нулю,
если этот предел существует и конечен.
называется предел отношения приращения
функции к приращению аргумента при
стремлении приращения аргумента к нулю,
если этот предел существует и конечен.
Если
![]() считать приращением функции
,
соответствующим приращению аргумента
считать приращением функции
,
соответствующим приращению аргумента
![]() ,
то имеет место равенство
,
то имеет место равенство
![]() .
В соответствии с определением производной
.
В соответствии с определением производной
![]() ,
,
здесь
![]() обозначение производной (первой
производной), позднее будут введены
другие обозначения производных.
обозначение производной (первой
производной), позднее будут введены
другие обозначения производных.
Определение 2.
Функция
называется дифференцируемой в точке
представлено в виде
![]() ,
причем
,
причем
![]() не зависит от
,
а
не зависит от
,
а
![]() бесконечно малая при
бесконечно малая при
![]() более высокого порядка малости по
сравнению с
,
то есть
более высокого порядка малости по
сравнению с
,
то есть
![]() .
.
Рассмотрим, чему
равняется
,
для чего поделим полученное равенство
на
и перейдем к пределу при
![]() .
Очевидно
.
Очевидно
![]() .
.
Итак,
![]() .
.
Поскольку бесконечно малая более высокого порядка малости, чем , при малых значениях второе слагаемое правой части формулы для приращения значительно меньше по сравнению с первым, то есть при малых значениях приближенно можно считать
![]() ,
или
,
или
![]() ,
где
,
где
![]() -
дифференциал функции.
-
дифференциал функции.
Таким образом,
дифференциал функции является основной
частью ее приращения. Для удобства
записи дифференциала функции вводят
обозначение
![]() , тогда
, тогда
![]() ,
что позволяет ввести еще одно обозначение
производной
,
что позволяет ввести еще одно обозначение
производной
![]() .
.
Геометрический смысл производной
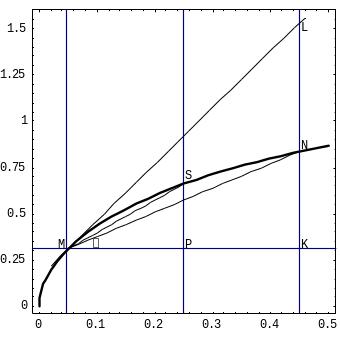
Рисунок 34.
Возьмем две точки
кривой
:
![]() и
и
![]() ,
соединим их хордой (смотри рисунок).
Пусть
,
соединим их хордой (смотри рисунок).
Пусть
![]() - угол между хордой
- угол между хордой
![]() и осью
и осью
![]() ,
тогда
,
тогда
![]() .
Уменьшим
вдвое, при этом точка
.
Уменьшим
вдвое, при этом точка
![]() ,
смещаясь вдоль кривой, займет положение
,
смещаясь вдоль кривой, займет положение
![]() .
Обозначим угол между хордой
.
Обозначим угол между хордой
![]() и осью абсцисс
и осью абсцисс
![]() .
Для рассматриваемого случая
.
Для рассматриваемого случая
![]() ,
что видно из рисунка. Если далее уменьшать
приращение аргумента
,
точка
еще более приближается к точке
,
что видно из рисунка. Если далее уменьшать
приращение аргумента
,
точка
еще более приближается к точке
![]() ,
изменяется угол хорды, соединяющей
точки, с осью
.
Ясно, что при
точки
и
в конечном итоге сливаются, хорда
становится касательной к кривой
,
изменяется угол хорды, соединяющей
точки, с осью
.
Ясно, что при
точки
и
в конечном итоге сливаются, хорда
становится касательной к кривой
![]() ,
а угол наклона хорды становится углом
,
а угол наклона хорды становится углом
![]() касательной к кривой с осью
.
Таким образом, из
касательной к кривой с осью
.
Таким образом, из
![]() следует
следует
![]() .
.
Итак, геометрический смысл производной функции в заданной точке – это тангенс угла между касательной к кривой в указанной точке и осью абсцисс.
Физический (механический) смысл производной
Из школьного курса физики известно, что средняя скорость движения равна отношению пройденного пути ко времени его прохождения то есть
![]() ,
где
,
где
![]() пройденный
путь,
пройденный
путь,
![]() время
его прохождения. Известно также, что
средняя скорость практически не дает
информации о движении объекта. В самом
деле, если человек, желающий сесть в
поезд на станции, находящейся посредине
между начальным и конечным пунктами
движения, знает, что поезд проходит весь
путь, скажем за 16 часов, то он придет на
станцию через восемь часов после начала
движения поезда из начального пункта
и на поезд может опоздать. Дело в том,
что поезд практически никогда не идет
со средней скоростью. На станциях его
скорость равна нулю, затем он набирает
скорость, некоторое время идет с
постоянной скоростью, затем начинает
скорость уменьшать при подходе к
очередной станции и так далее. Если на
первом участке пути скорость поезда
выше, чем на втором, и остановок меньше,
то, первую половину пути он пройдет
быстрее, чем вторую. Знание средней
скорости поезда нашего пассажира
подведет. Какая же скорость дает полную
информацию о движении объекта? Это
мгновенная скорость движения, или
скорость в данный момент времени. Именно
она равняется нулю во время пребывания
поезда на станциях, она возрастает при
отходе его со станций, она же уменьшается
при подходе к станциям. Как подсчитать
мгновенную скорость движения? Математика
дает ответ на этот вопрос. Нужно подсчитать
предел средней скорости при
время
его прохождения. Известно также, что
средняя скорость практически не дает
информации о движении объекта. В самом
деле, если человек, желающий сесть в
поезд на станции, находящейся посредине
между начальным и конечным пунктами
движения, знает, что поезд проходит весь
путь, скажем за 16 часов, то он придет на
станцию через восемь часов после начала
движения поезда из начального пункта
и на поезд может опоздать. Дело в том,
что поезд практически никогда не идет
со средней скоростью. На станциях его
скорость равна нулю, затем он набирает
скорость, некоторое время идет с
постоянной скоростью, затем начинает
скорость уменьшать при подходе к
очередной станции и так далее. Если на
первом участке пути скорость поезда
выше, чем на втором, и остановок меньше,
то, первую половину пути он пройдет
быстрее, чем вторую. Знание средней
скорости поезда нашего пассажира
подведет. Какая же скорость дает полную
информацию о движении объекта? Это
мгновенная скорость движения, или
скорость в данный момент времени. Именно
она равняется нулю во время пребывания
поезда на станциях, она возрастает при
отходе его со станций, она же уменьшается
при подходе к станциям. Как подсчитать
мгновенную скорость движения? Математика
дает ответ на этот вопрос. Нужно подсчитать
предел средней скорости при
![]() .
Итак,
.
Итак,
![]() .
.
Следовательно, скорость движения в каждый момент времени равна производной от пути по времени. В этом заключается физический смысл производной. Если абстрагироваться от реального движения, то можно утверждать, что физический смысл производной – это скорость изменения функции.
Теорема. Дифференцируемая на некотором интервале функция непрерывна в нем.
Доказательство.
Поскольку функция
![]() дифференцируема на некотором интервале,
ее производная, а следовательно,
дифференцируема на некотором интервале,
ее производная, а следовательно,
![]() имеет во всех его точках конечное
значение, но это возможно только при
имеет во всех его точках конечное
значение, но это возможно только при
![]() ,
в противном случае
,
в противном случае
![]() .
Таким образом,
.
Таким образом,
![]() ,
что совпадает с одним из определений
непрерывности функции.
,
что совпадает с одним из определений
непрерывности функции.
