Тема 12. Производная и дифференциал функции двух переменных. Лекция План лекции

1.Понятие функции нескольких переменных (двух, трех).

2.Предел и непрерывность функции двух переменных.

3.Частные производные функции двух переменных.

4.Полный дифференциал функции двух переменных.

5.Дифференциал высшего порядка функции двух переменных.

6.Дифференцирование сложной функции двух переменных.

7.Дифференцирование неявной функции.

1.Если x,y – стороны прямоугольника, то его площадь S=xy зависит от двух переменных x,y (S-функция двух переменных); если x,y,z - стороны прямоугольного параллелепипеда, то его объем V=xyz зависит уже от трех переменных x,y,z(V- функция трех переменных). Существует зависимость переменной и от большего числа независимых переменных. Если G – некоторое множеcтво точек (пусть - это множество точек плоскости XOY) , то произвольной точке M(x,y) G можно поставить в соответствие единственное число f(M)=u говорят: на множестве G задана функция с множеством значений U u=f(x,y). Множество G - это область определения функции, множество U (чисел вида f(x,y), ) - это множество значений функции u=f(x;y). Область определения G функции u=f(x,y) в простейших случаях представляет собой или часть плоскости, ограниченную замкнутой кривой (точки кривой (границы области) либо принадлежат, либо не принадлежат области G); или совокупность нескольких частей плоскости. Геометрическим изображением множества значений U функции u=f(x,y) (множества точек пространства с координатами (x,y,z)) в прямоугольной системе координат (графиком функции) является некоторая поверхность. Существуют функции большего числа переменных: u=f(x,y,z,…t). Функции нескольких переменных задаются формулами. Множество точек M(x,y), для которых имеет смысл формула, называется естественной областью определения. Например, - это круг с центром в начале координат и радиусом, равным единице. Линия уровня функции u=f(x,y) - это линия f(x,y)=С на плоскости XOY , в точках которой функция сохраняет постоянное значение: u=С . Например, для функции уравнение семейства линий уровня имеет вид . При различных действительных значениях С получаем концентрические окружности с центром в начале координат. Поверхность уровня функции u=f(x,y,z)-это поверхность f(x,y,z)=С , в точках которой функция сохраняет постоянное значение: u=С. Например, для функции уравнение семейства поверхностей уровня имеет вид при С=0 –это конус, при С>0 –это семейство гиперболоидов, при С<0 – семейство двуполостных гиперболоидов.

2.Окрестностью точки называется любой открытый (без включения границ) круг с центром в точке и радиусом R. Если , имеем - окрестность точки или множество всех точек с координатами , . Пределом функции f(M) при называется число А такое, что для любой последовательности точек такой, что , выполняется равенство 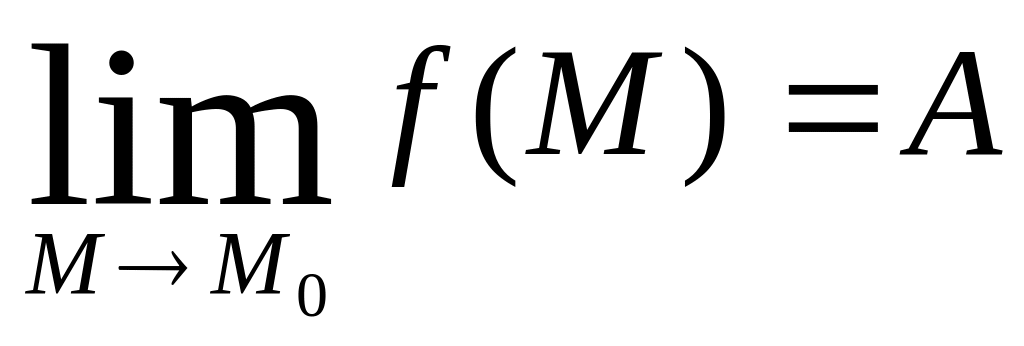: (1). Все теоремы функции одной переменной справедливы. Функция f(M)=f(x,y) называется непрерывной в точке М, если выполняется: или (2). Если функция непрерывна в каждой точке области G, то она непрерывна во всей области G.

3.Пусть функция u=f(x,y) определена в некоторой окрестности точки . Положим , тогда функция - это функция одной переменной «х». Производная функции по переменной «х» в точке - это частная производная по «х» от в точке : 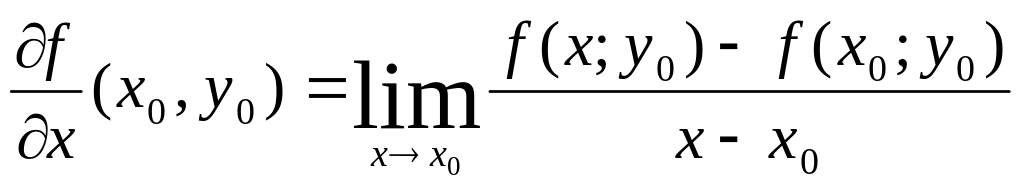или ,

(3). Частная производная по переменной y: (4). Иначе говоря, - это производная функции f(x;y) при - константе, - это производная функции f(x;y) при - константе. Например, для функции Частные производные также являются функциями двух переменных, существуют вторые частные производные: (5),

(если первые производные непрерывны, то вторые производные по разным переменным (смешанные производные) равны между собой: (6). Например, для функции

Геометрически – первые частные производные функции u=f(x,y) – это угловые коэффициенты касательных к линиям пересечения поверхности u=f(x,y) с плоскостями, параллельными координатным плоскостям ZOY;XOX и проходящим соответственно через точку

4.Для функции u=f(x,y) дадим координатам точки M(x;y) (аргументам) соответствующие приращения Приращение функции u=f(x,y), соответствующее этим приращениям: . Функция

u=f(x,y) дифференцируема в точке M(x;y), если ее приращение в данной точке можно представить в виде: (7). А,В – это некоторые числа, не зависящие от , - бесконечно малые функции при ; поэтому в (7) вторые слагаемые – бесконечно – малые величины . Выражение (8) – это главная линейная часть приращения функции u=f(x,y). Дифференциал функции двух переменных – это главная линейная часть ее приращения : . Для дифференцируемой функции u=f(x,y) точке M(x;y)функция u=f(x,y) имеет частные производные по переменным x;y и . Полный дифференциал функции u=f(x,y) : или . Положим : (9) – полный дифференциал функции двух переменных. Например, для функции u=cos(2x-3y):

Из (5) для функции : (а). Обозначим , тогда (10) - это полный дифференциал некоторой функции U. Обратная задача: когда выражение (11) становится полным дифференциалом некоторой функции? Условие: для того, чтобы (11) было полным дифференциалом некоторой функции U=U (x;y), необходимо и достаточно: (12) . Из (а) : , выполняется (12).

Свойства: [1]. , [2]. ,

[3]. , [4]. . Например, .

5.Дифференциал второго порядка функции двух переменных – это дифференциал от полного дифференциала :

или . Например, для функции :

,

. Далее можно найти дифференциал третьего порядка и т. д.

6. Если функции непрерывные, дифференцируемые, то - это функция одной переменной «t» , тоже дифференцируема и имеет производную по переменной «t». Для вычисления дадим переменной «t» приращение , тогда и переменные x,y,z получат приращения : (см. выше). Разделим все члены равенства на ; при : , (так как все рассматриваемые функции непрерывны). Перейдя к пределу, получим:

или - формула дифференцирования сложной функции. Например, найти , если : =

, выразим x;y через переменную «t»: .

7. Функция F(x;y)=0 (13) неявная, если уравнение (13) нельзя разрешить относительно переменной ‘y’, например, - неявная функция. Считая «y» функцией от «x», дифференцируем (13) по формуле производной сложной функции: - формула дифференцирования неявной функции. Например, .