Математика Специальность «Информатика» список литературы

1. Р.А. Александрова. Математика. Учебное пособие. Изд-во РГУ им. И. Канта, 2007 г. (РГУ).

2. Практическое руководство к решению задач по высшей математике. Линейная алгебра, векторная алгебра, аналитическая геометрия, введение в математический анализ, производная и ее приложения: учеб. пособие, 2007. (РГУ).

3.Математика, ч.1, справочник/ сост. Р.А.Александрова: Изд-во РГУ им. И .Канта, 2010.-41 с.

4. Данко П. Е. Высшая математика в упражнениях и задачах с решениями : в 2 ч. : учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М. : ОНИКС 21 век : Мир и образование, 2003 - Ч. 1. - 6-е изд. - 304 с. - ISBN 5-94666-008-Х. - ISBN 5-329-00326-1. (имеется в РГУ)

5. Данко П. Е. Высшая математика в упражнениях и задачах c решениями : в 2ч. : учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М. : ОНИКС 21 век : Мир и образование, 2003 - Ч. 2. - , 6-е изд. - 416 с. - ISBN 5-94666-009-8. - ISBN 5-329-00327-Х. (имеется в РГУ)

Содержание курса

Тема I -множества План лекции

1. Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой.

2. Операции с числовыми множествами (объединение, пересечение).

3. Декартово произведение множеств.

Конспект лекции.

1. Множество – основное понятие, оно не определяется, вводится на примерах: множество жителей города - конечное, множество натуральных чисел N={1;2;3;…n…}-бесконечное. Каждое множество состоит из элементов: a;b;c;…m;1;2;3;…n…; элемент а принадлежит множеству А ( ); если В={x| }, то -пустое. Множества чисел, расположенных между двумя данными числами, иллюстрируются числовой прямой: прямой линией с началом координат (точкой О), направлениями и масштабом: (множество действительных – чисел R= ; отрезок - ; интервал – (a;b)={x|a<x<b}; полуинтервалы - и ; лучи - и ; открытые лучи - и . Для множеств А={2;4;6;8} и B={4;6}: все элементы В являются элементами множества А; множество В –это подмножество (правильная часть) множества А: ; Связь множества и его подмножества –это отношение включения, для него выполняются свойства: [1]. - рефлексивности; [2]. Из и следует - транзитивности; [3]. . Отношение иллюстрируется рисунком, где каждое множество изображается в виде овала; это диаграммы (круги) Эйлера – Венна. Если для множеств для А и В выполняется и , то А и В состоят из одних и тех же элементов: ; А и В связаны отношением равенства, свойства: [4]. А= А –рефлексивности; [5]. Из А=В следует В=А –симметричности; [6]. Из А=В и В=С следует А=С –транзитивности.

2. Объединение множеств А и В – это новое множество С, состоящее из тех и только тех элементов, каждый из которых принадлежит хотя бы одному из множеств А и В: или (союз «или» имеет «неразделительный» смысл: в объединение А и В включены элементы, принадлежащие хотя бы одному из множеств). Понятие объединения двух множеств распространяется и на большее число множеств. Свойства: [1]. А В=В ; [2]. . Например, для А=[2;6) и B=( ;3] объединение - это множество С=А В=[2;6) ;3]=(- ;6). Объединение множеств используется при решении, например, неравенств первой степени: для неравенства |х-4|>1 надо найти множество А={х||х-4|>1}, Так как неравенство |х-4|>1 равносильно совокупности двух неравенств (a) х-4>1 или (b)х-4<-1 (х>5 или х<3), то {x||x-4|>1}={x|x>5} {x|x<3}=(5; ) (- ;3). Пересечение множеств А и В – это новое множество С, состоящее из тех и только тех элементов, которые принадлежат и А, и В: .Свойства: [3].A B=B A; [4]. A (B C)=(A B) C. Например, пересечение А=[2;6) и B=( ;3] –это множество С=А В=[2;6) ( ;3]=[2;3]. Операция пересечения множеств также используется при решении неравенств первой степени: для неравенства |x-4|<1 надо найти множество А={x||x-4|<1}. Неравенство |x-4|<1 равносильно двойному неравенству –1<x-4<1, поэтому x-4>-1, х>3 (а); x-4<1, х<5 (b) и {x||x-4|<1}={x|x<5} {x|x>3} = [5]. Если два множества не имеют общих элементов, то А В= (множества непересекающиеся). [6]. A =A; A = .Разность множеств А и В – это новое множество С, содержащее те и только те элементы, которые принадлежат множеству А, но не принадлежат множеству В: А\B=C, A\B={x|x A,x B}. Если же В А, то разность A\B называется дополнением множества В до множества А: .Операции объединения и пересечения множеств являются основой для разбиения множества на классы. При разбиении, например, множества U- всех треугольников на 2 класса при помощи одного свойства «быть равносторонним» из U выделяется подмножество А «равносторонних треугольников», остается подмножество «разносторонних треугольников», при этом: Свойство «быть равносторонним» разбило множество треугольников U на два класса. Разбиение множества на попарно-непересекающиеся множества называется разбиением множества на классы, полученные классы называются классами разбиения.

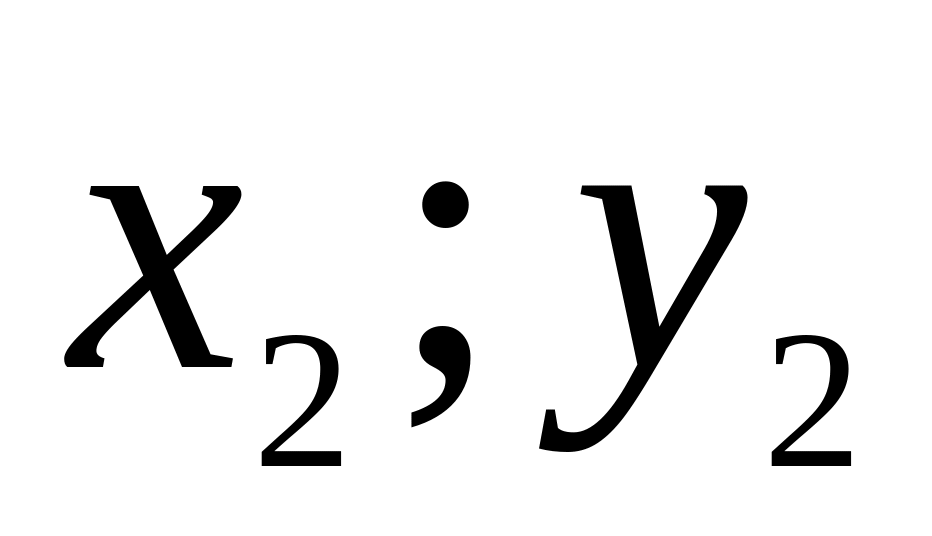3.Два элемента множества x и y образуют упорядоченную пару: (x;y); в паре (x;y) элемент (х) - первая компонента, (y) - вторая компонента. Равные упорядоченные пары - это пары вида и ( ) при ; если x y, то пары (x,y) и (y,x) различны. Если компоненты х и y принадлежат разным множествам ( ), то можно построить декартово произведение множеcтв X и Y: Х={2,4}, Y={a,b,c}, декартово произведение : {(2;a); (4;a);(2;b);(4;b);(2;c);(4;c)}. Геометрически. если то каждой паре (x,y) соответствует одна и только одна точка плоскости в данной системе координат, и обратно, каждой точке плоскости соответствует одна и только одна пара действительных чисел. Декартово произведение множеств X и Y –это множество всех упорядоченных пар вида (x,y) таких, что : X Y={(x,y)|x .Свойства: [1].X , [2]. X

Декартово произведение множеств изображается в виде чертежа: на горизонтальной оси откладывают элементы множества Х, на вертикальной оси, пересекающей горизонтальную ось под прямым углом в точке О – элементы множества Y. Тогда точка плоскости, первая координата которой х , а вторая y , является элементом декартова произведения. Например, декартово произведение множеств Х={3,4,5} и Y=[-2,4) изображено на рисунке (Рис.1):

Рис. 1

Частным случаем является составление декартова произведения множеств X и Y, таких, что X=Y, т.е. X и {(x;y)|x X,y X}; это декартов квадрат, обозначается ; декартов квадрат множества Х - это множество упорядоченных пар, обе компоненты пар выбираются из одного множества Х.