
- •Предел функции. Свойства пределов
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов функций
- •Предел суммы двух функций равен сумме пределов этих функций, если они существуют.
- •Предел произведения двух функций равен произведению их пределов, если они существуют.
- •Второй замечательный предел и его следствия
- •Непрерывность функции
- •Свойства непрерывных функций
- •Точки разрыва функции
- •Вычисление пределов
- •Правила вычисления предела
Вычисление пределов
Вначале выясним, в чем смысл вычисления пределов? В точках, где функция определена и непрерывна, соответствующий предел можно получить, вычислив ее значение. Особый подход к вычислению предела необходим, когда желательно знать поведение функции в окрестности особой точки, или установить, как ведет себя функция при стремлении ее аргумента к бесконечности.
Рассмотрим функции
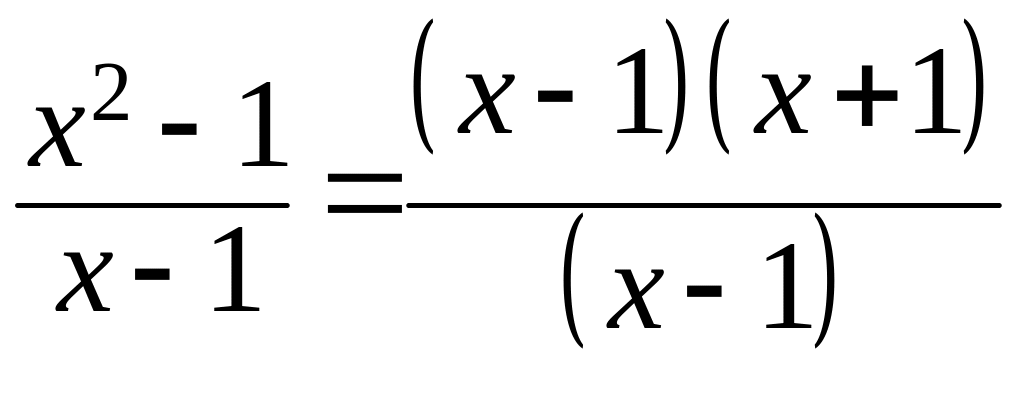 и
и
![]() .
Последняя получена в результате
формального сокращения числителя и
знаменателя первой на множитель
.
Последняя получена в результате
формального сокращения числителя и
знаменателя первой на множитель
![]() .
Это разные функции, так как имеют разные
области существования, хотя их значения
совпадают повсюду, кроме точки
.
Это разные функции, так как имеют разные
области существования, хотя их значения
совпадают повсюду, кроме точки
![]() .
В этой точке первая функция не существует
(деление на ноль), вторая равна 2. Теперь
вычислим предел
.
В этой точке первая функция не существует
(деление на ноль), вторая равна 2. Теперь
вычислим предел
![]() .
Рассмотрим последовательность действий
.
Рассмотрим последовательность действий
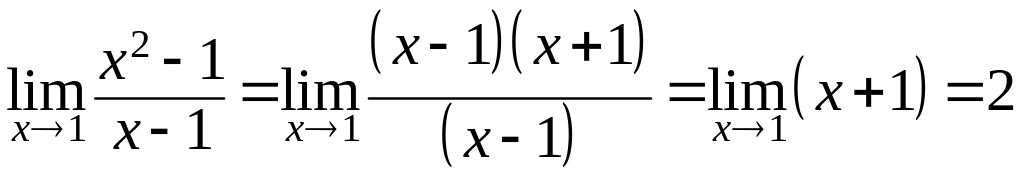 под знаком предела. Здесь мы заменяем
одну функцию на другую в той области,
где они совпадают, ибо при вычислении
предела
стремится к предельной точке 1, не попадая
в саму эту точку. Итак, рассматриваемая
функция в точке 1 не существует, но
стремится к значению 2 при
.
под знаком предела. Здесь мы заменяем
одну функцию на другую в той области,
где они совпадают, ибо при вычислении
предела
стремится к предельной точке 1, не попадая
в саму эту точку. Итак, рассматриваемая
функция в точке 1 не существует, но
стремится к значению 2 при
.
Исследуем
 .
Он равен 3, так как
.
Он равен 3, так как
![]() и
и
![]() являются бесконечно малыми при
являются бесконечно малыми при
![]() .
Сокращение на
.
Сокращение на
![]() также законно, поскольку
также законно, поскольку
![]() ,
а только стремится к ней, то есть принимает
сколь угодно большие, но конечные
значения.
,
а только стремится к ней, то есть принимает
сколь угодно большие, но конечные
значения.
Правила вычисления предела
Чтобы вычислить
![]() ,
необходимо.
,
необходимо.
Попробовать подставить в функцию, стоящую под знаком предела,
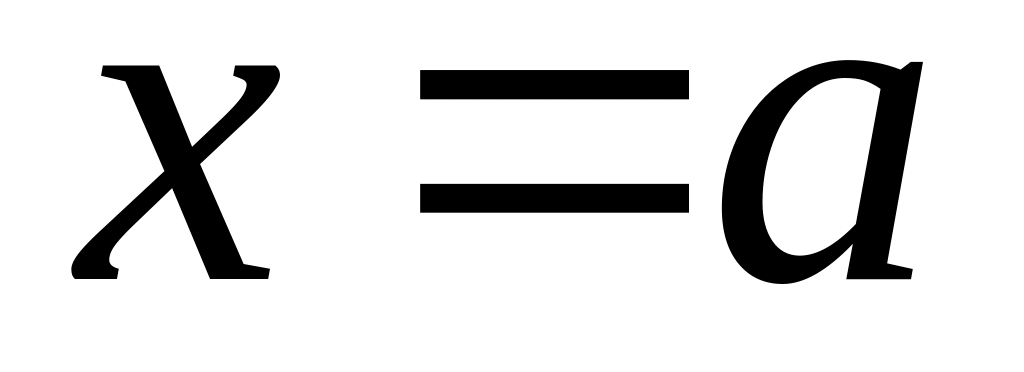 .
Если функция в этой точке непрерывна,
в соответствии формулой
предел равен числу
.
Если функция в этой точке непрерывна,
в соответствии формулой
предел равен числу
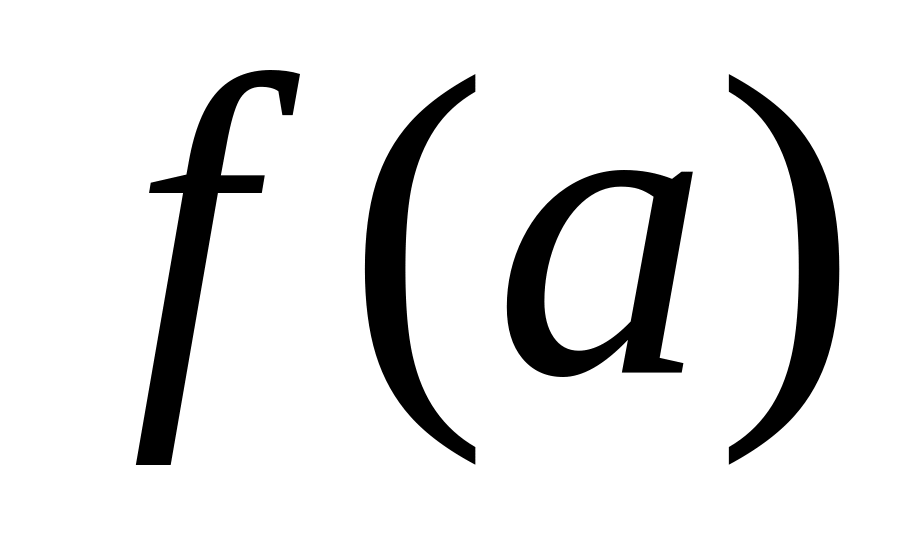 .
.Если точка не входит в область определения функции, то конечный предел может не существовать, и если абсолютная величина функции неограниченно увеличивается при стремлении переменной к , то пределом является бесконечность.
Если в результате подстановки получается неопределенность, то есть выражение вида
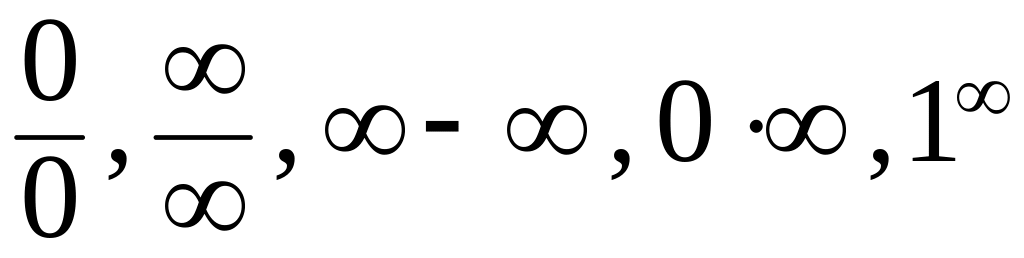 , следует раскрыть эту неопределенность,
сделав сокращения, или привести
получаемое выражение к замечательному
пределу или его следствию.
, следует раскрыть эту неопределенность,
сделав сокращения, или привести
получаемое выражение к замечательному
пределу или его следствию.
Примеры.
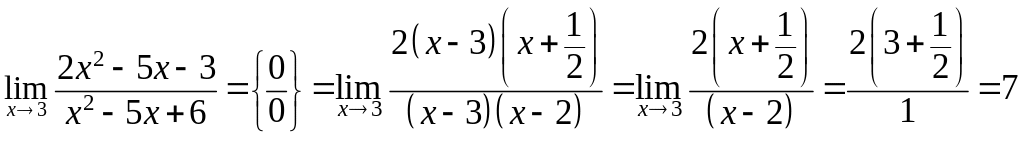 .
.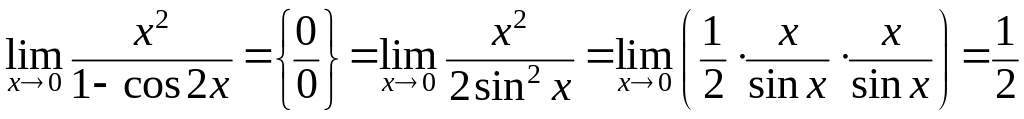 .
.
Неопределенности
![]() показывает, что в числителе и знаменателе
присутствуют бесконечно большие функции.
Чтобы избавиться от них следует вынести
самую большую величину в числителе и
знаменателе за скобки, произвести
сокращение, после чего еще раз применить
пункт 1 правил.
показывает, что в числителе и знаменателе
присутствуют бесконечно большие функции.
Чтобы избавиться от них следует вынести
самую большую величину в числителе и
знаменателе за скобки, произвести
сокращение, после чего еще раз применить
пункт 1 правил.
Примеры.
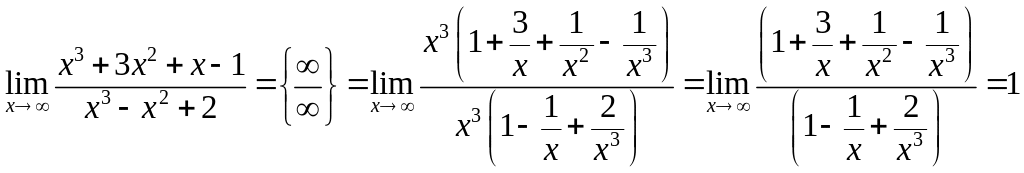 .
. .
.
Неопределенности
![]() приводятся вначале к виду
приводятся вначале к виду
![]() или
,
затем раскрываются одним из перечисленных
выше способов.
или
,
затем раскрываются одним из перечисленных
выше способов.
Примеры.
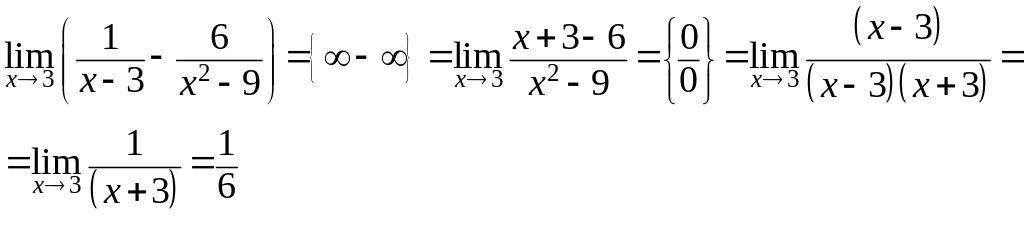
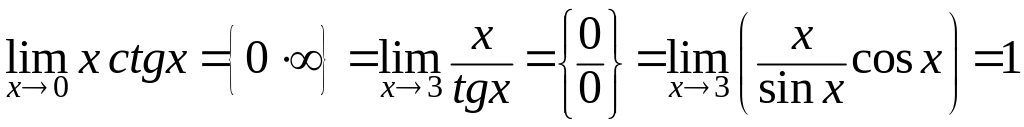 .
.Проверить непрерывность функции
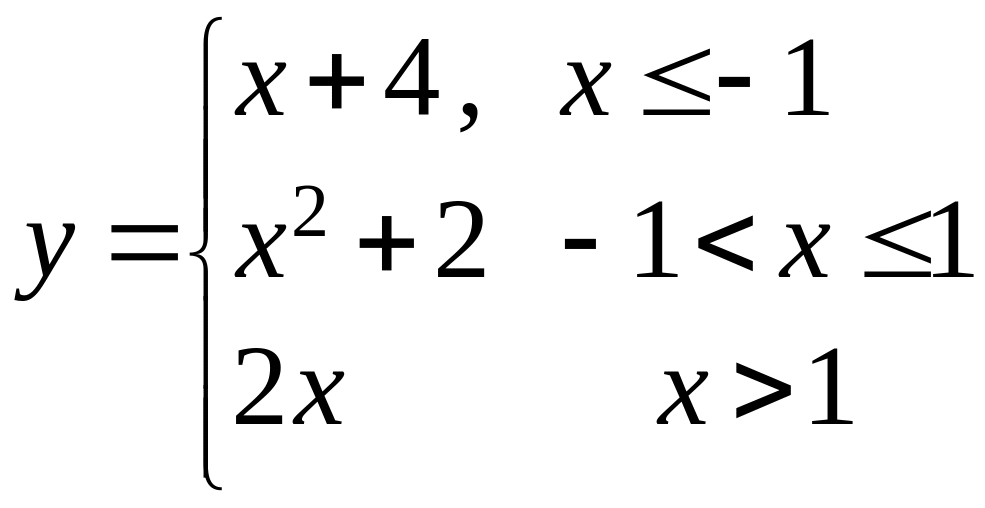 .
.
Поскольку функции
![]() ,
,
![]() и
и
![]() непрерывны в областях их задания,
достаточно рассмотреть функцию
непрерывны в областях их задания,
достаточно рассмотреть функцию
![]() в точках стыковки этих функций. Итак,
для
имеем
в точках стыковки этих функций. Итак,
для
имеем
![]() ,
,
![]() ,
,
![]() .
.
Функция в этой точке непрерывна согласно определению 4.
Для
имеем
![]() ,
,
![]() ,
,
![]() .
Условие непрерывности в точке
не выполняется.
.
Условие непрерывности в точке
не выполняется.
Следовательно, функция непрерывна на всей числовой оси за исключением точки , где она имеет конечный разрыв со скачком
(-1).
