
- •Предел функции. Свойства пределов
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов функций
- •Предел суммы двух функций равен сумме пределов этих функций, если они существуют.
- •Предел произведения двух функций равен произведению их пределов, если они существуют.
- •Второй замечательный предел и его следствия
- •Непрерывность функции
- •Свойства непрерывных функций
- •Точки разрыва функции
- •Вычисление пределов
- •Правила вычисления предела
Непрерывность функции
Определение 1.
Функция
непрерывна в точке
,
если предел этой функции при
равен значению функции в предельной
точке, то есть
![]() .
.
Применяя второе определение предела функции в точке, получим
Определение 2.
Функция
непрерывна в точке
,
если
![]() .
.
Определение 3.
Функция
![]() непрерывна в точке
,
если
непрерывна в точке
,
если
![]() ,
где
,
где
![]() приращение
аргумента функции (
приращение
аргумента функции (![]() ),
а
),
а
![]() – приращение функции, соответствующее
приращению ее аргумента
– приращение функции, соответствующее
приращению ее аргумента
![]() .
.
Доказательство следует из первого определения непрерывной функции
![]() Здесь первый из
пределов вычисляется с помощью определения
1, второй – как предел постоянной,
поскольку
Здесь первый из
пределов вычисляется с помощью определения
1, второй – как предел постоянной,
поскольку
![]() не зависит от
.
не зависит от
.
Определение 4. Функция непрерывна в точке , если
![]() .
.
Определение 5.
Функция
![]() непрерывна в некоторой области, если
она непрерывна во всех точках этой
области.
непрерывна в некоторой области, если
она непрерывна во всех точках этой
области.
Все степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции непрерывны в областях существования.
Свойства непрерывных функций
Сумма непрерывных функций – есть непрерывная функция.
Действительно, из
определения 1 непрерывности следует,
что если
и
![]() ,
то
,
то
![]() .
.
2). Произведение непрерывных функций есть функция непрерывная.
3). Частное непрерывных функций – функция непрерывная, если знаменатель в предельной точке не равен нулю.
Доказательства второго и третьего свойств также следует из свойств пределов.
4). Пусть функция
![]() непрерывна в точке
,
пусть функция
непрерывна в точке
,
пусть функция
![]() непрерывна в точке
непрерывна в точке
![]() .
Тогда функция
.
Тогда функция
![]() непрерывна в точке
.
непрерывна в точке
.
Очевидно, что
![]()
![]() .
.
Так как согласно
определению 3 непрерывности
![]() при
при
![]() и
и
![]() при
,
получим:
при
.
при
,
получим:
при
.
Таким образом, непрерывная функция от непрерывной функции есть функция непрерывная.
Пример.
Функция
![]() непрерывна во всех точках числовой оси,
так как функция
непрерывна во всех точках числовой оси,
так как функция
![]() непрерывна на
непрерывна на
![]() ,
а функция
,
а функция
![]() непрерывна
на множестве неотрицательных чисел.
непрерывна
на множестве неотрицательных чисел.
Точки разрыва функции
Определение. Точкой разрыва функции называется внутренняя точка области задания функции, в которой нарушается непрерывность функции.
Если в точке разрыва
функция, к тому же, не существует, ее
часто называют особой точкой. Так
функция
![]() существует на всей числовой оси, кроме
точки
существует на всей числовой оси, кроме
точки
![]() .
Эта точка – особая, и в ней функция
терпит разрыв.
.
Эта точка – особая, и в ней функция
терпит разрыв.
Разрыв может быть
конечным, если
![]() и
и
![]() принимают конечные, но не равные значения.
Разность между этими значениями называют
скачком функции в точке разрыва.
принимают конечные, но не равные значения.
Разность между этими значениями называют
скачком функции в точке разрыва.
Пример.
Функция
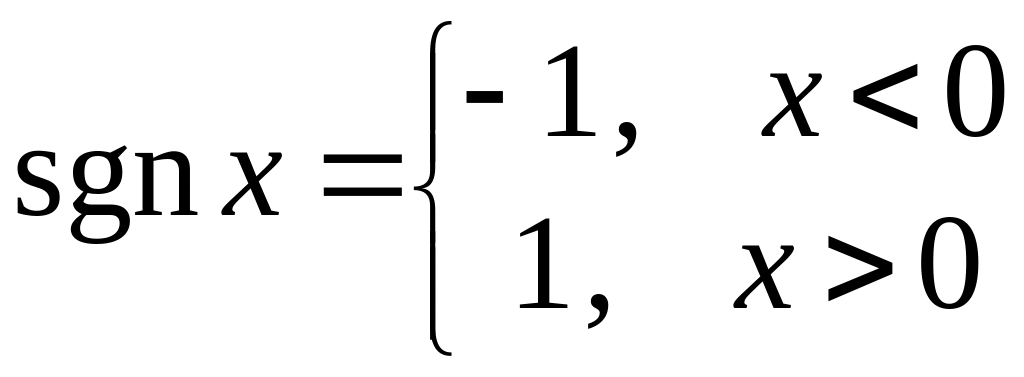 .
Очевидно,
.
Очевидно,
![]() ,
,
![]() .
.
Разрыв бесконечный, если левый, правый или оба предела бесконечны.
Пример.
![]() .
Имеем
.
Имеем
![]() ,
,
![]() .
.
Разрыв называется
устранимым, если
![]() и эти пределы конечны, но функция в
точке
не задана.
и эти пределы конечны, но функция в
точке
не задана.
Пример.
Функция
![]() не может быть задана при
(деление на ноль), однако и левый и правый
ее пределы равны 1, что следует из первого
замечательного предела.
не может быть задана при
(деление на ноль), однако и левый и правый
ее пределы равны 1, что следует из первого
замечательного предела.
Устранить этот
недостаток можно введением другой
функции
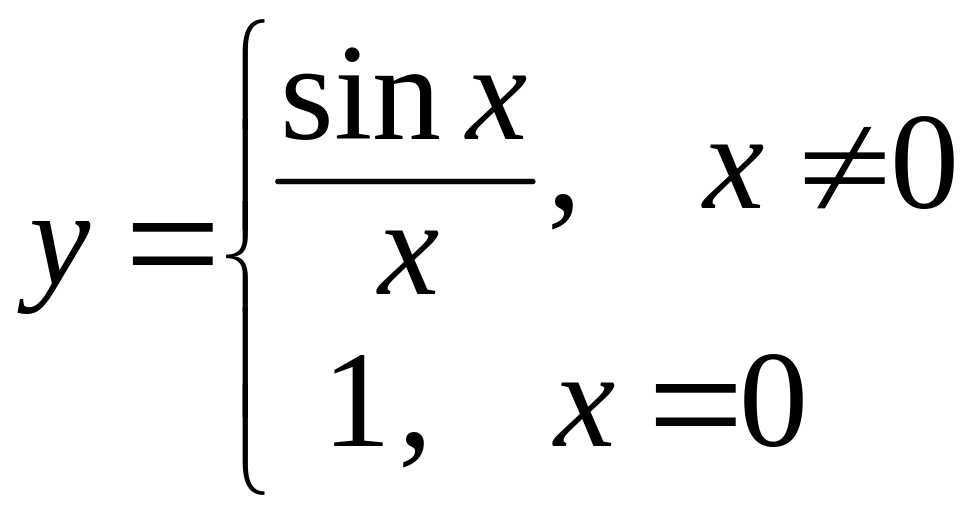 .
Эта функция совпадает с заданной во
всех точках, кроме 0, но она существует
и непрерывна на всей числовой оси, что
следует из свойств непрерывной функции.
.
Эта функция совпадает с заданной во
всех точках, кроме 0, но она существует
и непрерывна на всей числовой оси, что
следует из свойств непрерывной функции.
