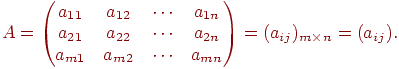ВОПРОС№1

Определение 1. Матрицей A называется любая прямоугольная таблица, составленная из чисел a_ij, которые называют элементами матрицы и обозначается

(2.1)

Заметим, что элементами матрицы могут быть не только числа. Представим себе, что вы описываете книги, которые стоят на вашей книжной полке. Пусть у вас на полке порядок и все книги стоят на строго определенных местах. Таблица, которая будет содержать описание вашей библиотеки (по полкам и следованию книг на полке), тоже будет матрицей. Но такая матрица будет не числовой. Другой пример. Вместо чисел стоят разные функции, объединенные между собой некоторой зависимостью. Полученная таблица также будет называться матрицей. Иными словами, Матрица, это любая прямоугольная таблица, составленная из однородных элементов. Здесь и далее мы будем говорить о матрицах, составленных из чисел.

Вместо круглых скобок для записи матриц применяют квадратные скобки или прямые двойные вертикальные линии

(2.1*)

Определение 2. Если в выражении (1) m = n, то говорят о квадратной матрице, а если m n, то о прямоугольной.

В зависимости от значений m и n различают некоторые специальные виды матриц:

1. Матрица - строка (или строковая матрица), состоящая из одной строки. Это прямоугольная матрица размером 1 × n.

2. A=(a₁₁ a₁₂ ... a_n).

3. Матрица - столбец (столбцевая матрица), состоящая только из одного столбца. Это также прямоугольная матрица размером m × 1

4. Матрица, состоящая из одного элемента. A=(a₁₁)_1×1=a₁₁.

5. Нулевая матрица, состоящая из одних нулей, в матричной алгебре играет роль 0, обозначается V.

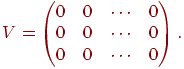
6. Единичная матрица, состоящая из нулей, кроме главной диагонали, на которой стоят единицы. Обозначается E и играет роль единицы в матричной алгебре

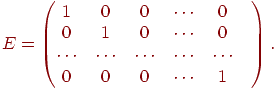
7. Диагональная матрица, квадратная порядка n, состоящая из нулей и на главной диагонали стоят не равные нулю элементы (не обязательно единицы)

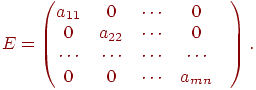
Важнейшей характеристикой квадратной матрицы является ее определитель или детерминант, который составляется из элементов матрицы и обозначается

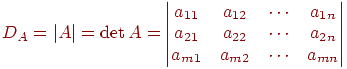
Очевидно, что D_E=1; D_V= .

Определение 3. Если detA 0, то матрица A называется невырожденной или не особенной.

Определение 4. Если detA = 0, то матрица A называется вырожденной или особенной.

Определение 5. Две матрицы A и B называются равными и пишут A = B, если они имеют одинаковые размеры и их соответствующие элементы равны, т.е.

Например, матрицы и равны, т.к. они равны по размеру и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. А вот матрицы и нельзя назвать равными, хотя детерминанты обеих матриц равны, и размеры матриц одинаковые, но не все элементы , стоящие на одних и тех же местах равны. Матрицы и 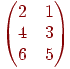разные, так как имеют разный размер. Первая матрица имеет размер 2х3, а вторая 3х2. Хотя количество элементов одинаковое – 6 и сами элементы одинаковые 1, 2, 3, 4, 5, 6, но они стоят на разных местах в каждой матрице. А вот матрицы и равны, согласно определению 5.

Определение 6. Если зафиксировать некоторое количество столбцов матрицы A и такое же количество ee строк, тогда элементы, стоящие на пересечении указанных столбцов и строк образуют квадратную матрицу n-го порядка, определитель которой Δk называется минором k–го порядка матрицы A.

ПРИМЕР:. Выписать три минора второго порядка матрицы

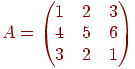
Решение.

ВОПРОС№2

Операции над матрицами

Равенство матриц. Две матрицы и одинакового размера m на n называются равными, если , i = 1,2,…,m, j=1,2,…,n.

Если матрицы A и B равны, то будем писать A=B.

Линейные операции. Суммой двух матриц A и B размера m на n называется матрица C размера m на n, элементы которой определяются равенством

Сумму матриц A и B будем обозначать C=A+B.

Матрица называется противоположной к матрице .

Теорема 2.1 Операция сложения матриц обладает следующими свойствами: для любых матриц и нулевой матрицы

1) A+B=B+A; (перестановочность или коммутативность операции сложения

2) (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)

3) A+O = O+A =A;

4) A+(-A)=(-A)+A=O.

Перечисленные выше свойства непосредственно вытекают из определения и доказываются по единой схеме.

Разностью матриц и называется матрица A+(-B).

Разность матриц A и B будем обозначать A-B.

Произведением матрицы на число называется матрица , элементы которой определены равенством

Произведение матрицы A на число будем обозначать .

Теорема 2.2 Операция умножения матрицы на число обладает следующими свойствами:

1) ;

2) ;

3) (Распределительное свойство относительно сложения матриц);

4) (Распределительное свойство относительно сложения чисел);

5) -A=(-1)A.

Все перечисленные свойства непосредственно вытекают из определения.

Операции сложения матриц и умножения матрицы на число позволяют для произвольных матриц одинакового размера и произвольных чисел однозначно определить матрицу 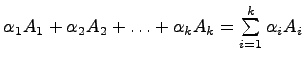, называемую линейной комбинацией матриц с коэффициентами .

Умножение матриц. Произведением матриц и называется матрица , элементы которой определены равенством

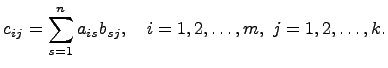
Произведение матриц A и B будем обозначать C=AB.

Из определения следует, что произведение AB определено лишь в том случае, когда число столбцов матрицы A совпадает с числом строк матрицы B. Это означает, что оба произведения AB и BA определены тогда и только тогда, когда матрицы A и B имеют размеры и соответственно. Следовательно равенство AB=BA возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.

Матрицы A и B называются перестановочными или коммутирующими, если AB=BA.

Теорема 2.3 Операция умножения матриц обладает следующими свойствами:

1) (AB)C=A(BC); (Свойство ассоциативности)

2) , для любого действительного числа

3) A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности), для любых матриц A, B, C, для которых левые части равенств имеют смысл.

Справедливость свойств 2) и 3) доказываются непосредственно.

В качестве иллюстрации приведём доказательство первого равенства свойства 3). Пусть , , . Матрицы A(B+C) и AB+AC имеют одинаковый размер - . Пусть - элемент матрицы A(B+C) в позиции (i,j), - элемент матрицы AB+AC в позиции (i,j), тогда

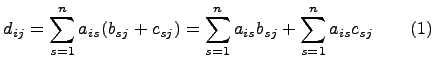
Из равенств (1) и (2) следует, что , что доказывает первое равенство свойства 3).

Подробное доказательство свойства 1) можно найти в учебнике В. А. Ильин, Г. Д. Ким "Линейная алгебра и аналитическая геометрия".

Заметим, что для любой матрицы и единичных матрицы и справедливо:

Транспонирование матриц. Пусть . Матрица называется транспонированной к матрице A, если

Транспонированная матрица также обозначается символами и .

Заметим, что при транспонировании матрицы её строки становятся столбцами матрицы , с теми же номерами, а столбцы - строками.

Теорема 2.4. Операция транспонирования матриц обладает следующими свойствами:

1) ;

2) , для любого действительного числа ;

3) ;

4) , для любых матриц A и B, для которых имеют смысл левые части равенств.

Свойства 1), 2), 4) непосредственно вытекают из определения.

Приведём доказательство свойства 3). Пусть и , при таком согласовании размеров матриц A и B произведения AB и существуют, при этом размеры и совпадают и равны . Пусть - элемент матрицы AB в позиции (i,j), - элемент матрицы , - элемент матрицы в позиции (i,j).

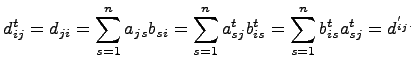
что доказывает справедливость свойства 3).

Примеры

Систему из m уравнений с n неизвестными

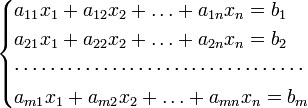
можно представить в матричном виде

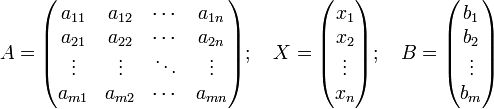
и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{- 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{- 1}AX = A ^{- 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{- 1}B.

Все правила, по которым проводятся операции над матрицами, выводятся из операций над системами уравнений.

ВОПРОС№3

1) Определитель 2 порядка: |a11 a12| |           | = a11*a22-a12*a21 |a21 a22| |2 5| |           | = 1 |1 3| 2) Определитель 3 порядка: |a11 a12 a13| |a21 a22 a23| = (a11*a22*a23+a12*a23*a31+a21*a32*a13)-(a13*a22*a31+a23*a32*a11+a12*a21*a33) |a31 a32 a33| | 2  1 4| | 5  7 2| = -140 |10 3 8|

Примеры: |1 123456789| |1 123456789| =0 |1 0 0| |0 1 0| = 1 |0 0 1| |1 2 3| |4 5 6| = 0 |5 7 9|

ВОПРОС№4

Свойства определителей

СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть

.

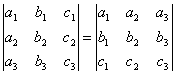СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,

.

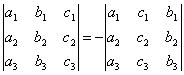СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,

.

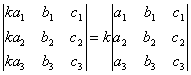СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

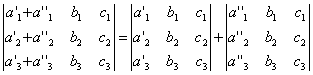
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,

.

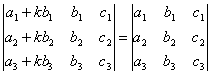Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.

Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.

СВОЙСТВО 9. Определитель

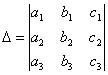
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.

Иначе говоря, имеют место следующие равенства:

, ,

, ,

,

ВОПРОС№5