5.16.3. Теоремы о сходимости несобственных интегралов

Вопрос о сходимости несобственного интеграла в ряде случаев можно решить без его вычисления. Это особенно важно, когда первообразную через элементарные функции в конечном виде выразить невозможно. Рассмотрим простейшие теоремы относительно сходимости несобственных интегралов с бесконечными пределами.

Теорема 1. Если и интеграл сходится, то сходится и интеграл Если при тех же предположениях интеграл расходится, то расходится и интеграл .

Доказательство производится следующим образом.

Так как

то первый интеграл при монотонно возрастает и ограничен. Поэтому существует конечный предел

Вторая часть теоремы доказывается аналогично:

Теорема 2. Если сходится интеграл то сходится и интеграл .

Не приводя доказательства этой теоремы, заметим что в первом интеграле суммируются площади, лежащие над и под осью абсцисс, а во втором интеграле площади под осью абсцисс учитываются со знаком минус. Поэтому первый интеграл сходится “труднее”: он может расходиться в тех случаях, когда второй интеграл сходится.

Если интеграл сходится, то интеграл называется абсолютно сходящимся.

Если интеграл сходится, а расходится, то первый интеграл называется условно сходящимся.

Теорема 3. Если и существует конечный ненулевой предел то интегралы , либо оба сходятся, либо оба расходятся.

Доказательство этой теоремы не приводим.

Наиболее часто при выяснии вопроса о сходимости несобственного интеграла выполняют сравнение его с интегралом от степенной функции

(5.16.7)

который сходится при p>1 и расходится при p

Действительно,

П р и м е р: Определить, сходится ли интеграл

Решение: 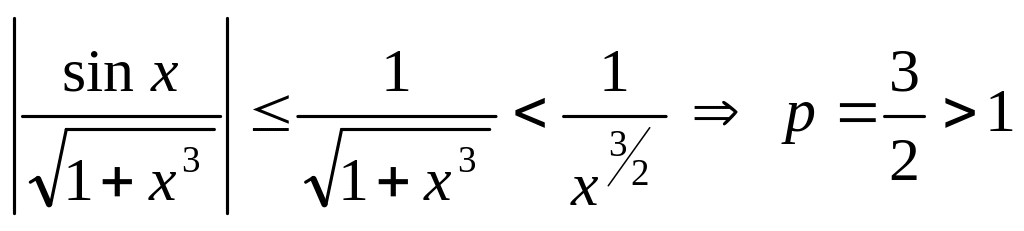(см. (5.16.7)). Следовательно, данный интеграл сходится абсолютно.

Теоремы, аналогично рассмотренным, справедливы и для несобственных интегралов от разрывных функций (сформулируйте их самостоятельно). При этом сравнение часто осуществляют с интегралом со степенной особенностью

который сходится при p<1 и расходится при p 1 (проверить самостоятельно).

Задание для самостоятельного решения.

1. Исследуйте на сходимость следующие несобственные интегралы:

а) б) в)

г) д) е)

2. Приведите примеры абсолютно сходящихся несобственных интегралов первого и второго рода.

17. Интеграл как функция пределов интегрирования. Понятие о специальных функциях, определяемых интегралами с переменным верхним пределом.

Определенный интеграл

можно рассматривать как функцию от а и b. Пусть a=const , а b обозначим через х. Тогда получим следующую функцию от х:

(5.17.1)

Дифференцируя (5.17.1) по х с учётом того, что получаем следующее правило дифференцирования определенного интеграла по переменному верхнему пределу:

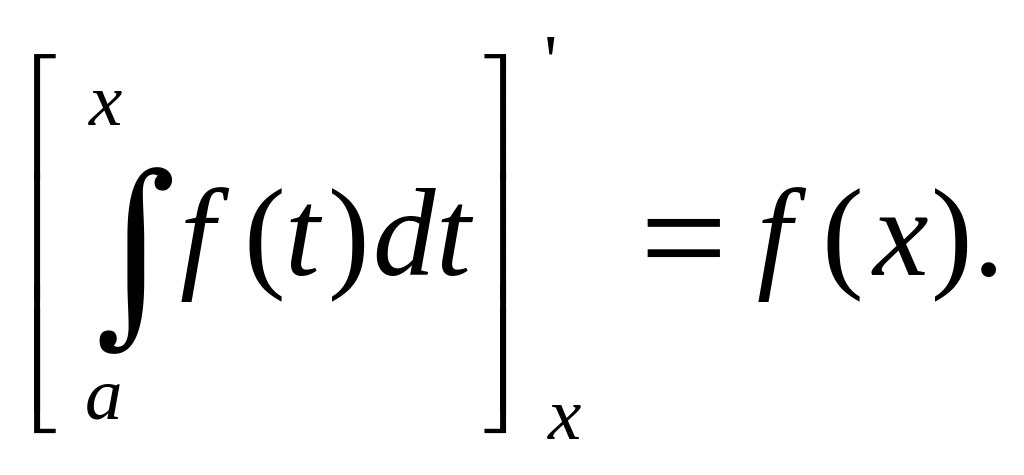(5.17.2)

Если верхний предел является функцией b(x), то

(5.17.3)

и вместо (5.17.2) будем иметь

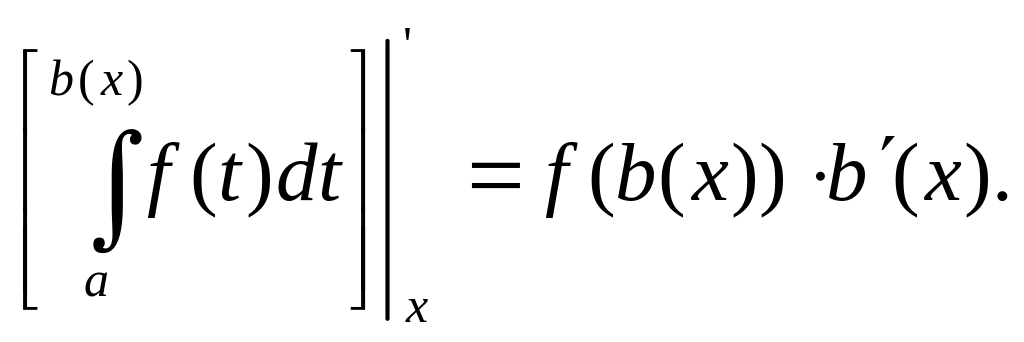
Задание для самостоятельного решения:

1. Как вычислить производную по х, если интегрирование в (5.17.3) выполняется от а(х) до b(x) ? Найдите эту производную.

2. Подумайте, каков геометрический смысл интеграла (5.17.1).

3. Найдите производную по х от интегралов:

а) 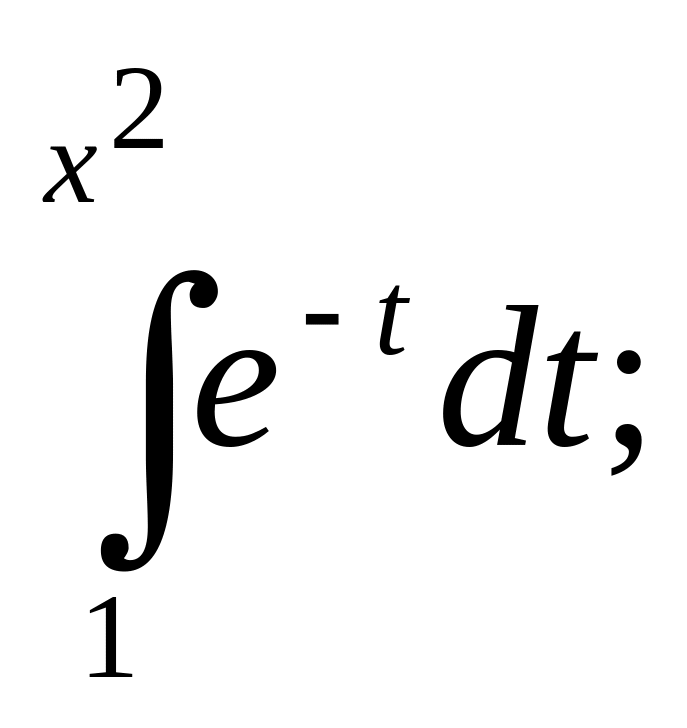б)

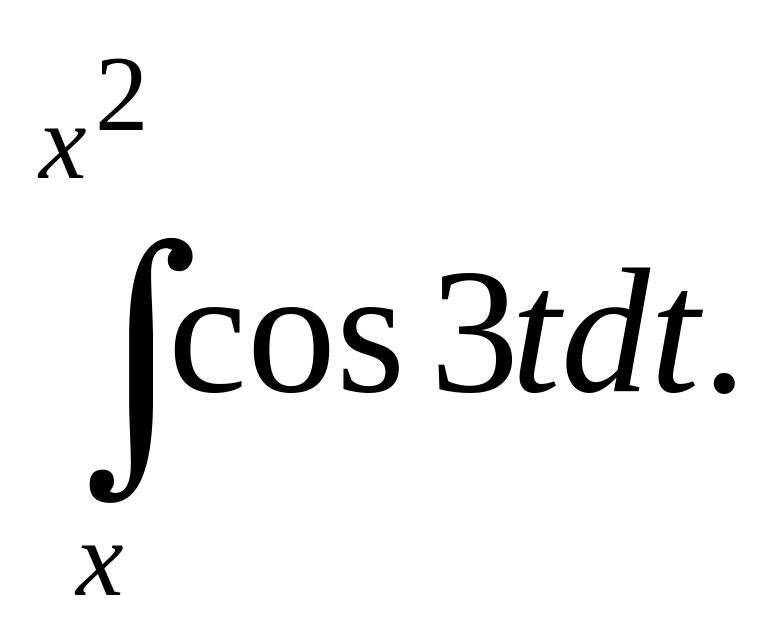
Производная от элементарной функции всегда является элементарной функцией. Первообразная же от элементарной функции не всегда оказывается элементарной функцией. В связи с тем , что многие задачи математики и механики связаны с изучением и таких первообразных, возникает необходимость рассмотрения так называемых специальных функций, задаваемых при помощи интегралов с переменным пределом.

Так, в теории вероятности важную роль играет функция

(5.17.4)

которая называется нормальной функцией распределения.

Так как

то функция (5.17.4) монотонно возрастает. В дальнейшем мы увидим, что Для значений функции составлены таблицы.

Функция интегральный синус определяется интегралом

Особенность подынтегральной функции при t=0 является устранимой.

Аналогично определяется интегральный логарифм:

Используются и другие функции, определяемые при помощи интеграла с переменным верхним пределом.