5.3. Разложение многочлена на множители в случае действительных и мнимых корней.
Уравнение вида
где
- многочлен степени n,
называется алгебраическим уравнением
n-ой степени (n-ого
порядка).
Теорема 1 (основная теорема алгебры). Всякое алгебраическое уравнение имеет, по крайней мере, один действительный или мнимый корень.
Эту теорему мы принимаем без доказательства.
Заметим, что коэффициенты многочлена могут быть мнимыми.
Теорема 2 (Безу). При делении
многочлена
на разность
получается остаток, равный
Для доказательства запишем тождество, соответствующее условию теоремы 2:
(5.3.1)
(здесь через r обозначен остаток от деления на ).
Полагая в (5.3.1)
получаем
что и требовалось доказать.
Следствие. Если число с является корнем многочлена , то он делится на разность без остатка.
Действительно,
Теорема 3. Всякий многочлен
разлагается в произведение п линейных
сомножителей вида
и множитель, равный коэффициенту при
Пусть
и
-
корень уравнения
=0.
Тогда согласно теореме Безу
разделится на
без остатка:
т.е.
Далее, пусть
-
корень уравнения
(такой корень, как и
существует
в силу основной теоремы алгебры). Тогда
аналогично предыдущему
где
имеет в качестве коэффициента при
старшей степени х величину
Таким
образом, имеем
Если продолжить цикл рассуждений, то мы придем к равенству
(5.3.2)
которое и следовало доказать.
Заметим, что с введением комплексных чисел изменяется взгляд на разрешимость уравнения =0: оно всегда имеет ровно п корней.
Среди корней многочлена могут быть кратные. Поэтому вместо (5.3.2) удобнее записать равенство
(5.3.3)
где среди чисел
нет одинаковых, а
Число
называется кратностью корня
.
Если все числа являются действительными, то формула (5.3.3) дает искомое разложение многочлена на линейные множители.
Однако, среди чисел могут быть и мнимые.
Оказывается, что если многочлен имеет только действительные коэффициенты, то все его мнимые корни образуют сопряженные пары.
Теорема 4. Если комплексное
число
- корень многочлена
с действительными коэффициентами, то
сопряженное число
тоже является корнем этого многочлена.
Для доказательства образуем многочлен
=
Этот многочлен имеет действительные
коэффициенты. Поэтому при делении
на
в остатке может получиться только
линейная функция с действительными
коэффициентами:
При
из этого тождества получаем
т.е.
откуда
Таким образом, многочлен
делится
на квадратный трехчлен (5.3.4) без остатка
и, следовательно, число
является его корнем.
На основании теоремы 4 разложение (5.3.3) в общем случае следует записывать так:
(5.3.5)
где
5.4. Разложение правильной рациональной дроби на простейшие дроби
Представление многочлена в виде (5.3.5)
используется при разложении правильной
рациональной дроби
на элементарные слагаемые вида
Считая, что знаменатель
согласно (5.3.5) может содержать линейные
и квадратичные множители, т.е.
записывают
разложение данной дроби на элементарные
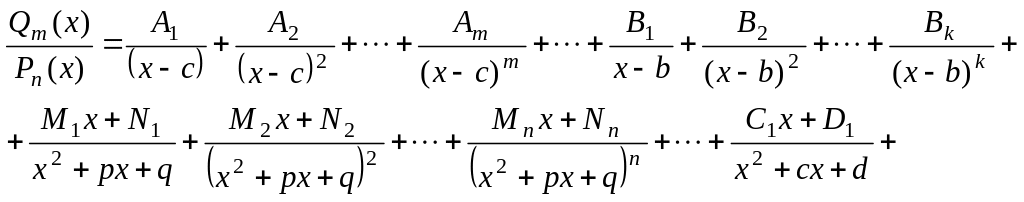
постоянные
находят методом неопределённых
коэффициентов из системы уравнений,
которая получается в результате
приравнивания
к числителю дроби, стоящей в правой
части (5.4.1), после приведения последней
к общему знаменателю
и
сравнения коэффициентов при одинаковых
степенях х.
Пример. Разложим на элементарные слагаемые дробь
Согласно (5.3.6) имеем
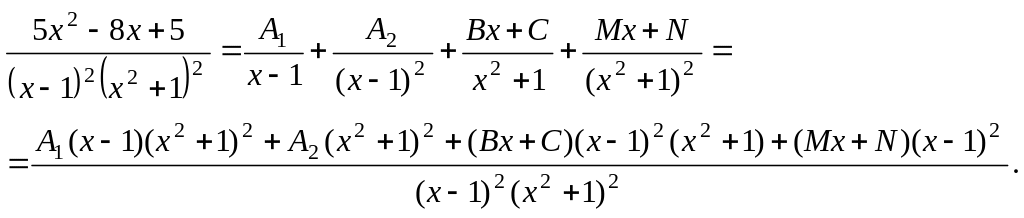
Тогда
Сравнивая коэффициенты многочленов, стоящих в левой и правой частях равенства, находим
Следовательно,
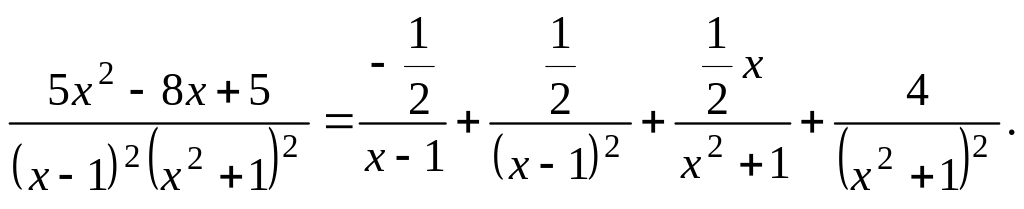
Приведенная схема разложения правильной рациональной дроби на элементарные слагаемые будет использована на практических занятиях при вычислении интегралов от рациональных дробей и в ряде других случаев.