Комплексные числа.

5.1. Основные понятия о комплексных числах.

Как известно, извлечение квадратного корня из действительного числа можно выполнить, когда это число неотрицательно. Однако такое мнение остаётся справедливым до тех пор, пока мы пользуемся лишь понятием действительного числа. Оказывается, что расширив понятие числа, можно придать конкретный смысл операции извлечения корня четной степени из любого числа.

В связи с изложенным вводится некая мнимая единица (символ)

(5.1.1)

удовлетворяющая условию

(5.1.2)

В соответствии с (5.1.1) естественно считать равным

Выражение вида

(5.1.3)

называется комплексным числом.

В дальнейшем комплексные числа будут представляться в различных формах. Вид комплексного числа (5.1.3) называется его алгебраической формой, х называется действительной частью, y – мнимой частью комплексного числа. При этом используются обозначения

Если х=0, то комплексное число z называется числом чисто мнимым. Если то его называют мнимым.

Комплексное число

называется сопряженным к числу (5.1.3).

Геометрически комплексное число изображается точкой плоскости с координатами х и y или соответствующим радиусом-вектором (Рис. 5.1). Комплексное число можно рассматривать как вектор в базисе (1, i).

z

r

y

x

x

0

Рис. 1

Действия над комплексными числами вводятся так, чтобы оставались в силе обычные законы алгебры и аксиома (5.1.2):

1. сложение

2. умножение на действительное число

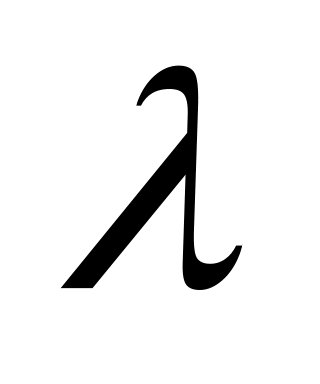
3. умножение комплексных чисел

Заметим, что при сложении и умножении спряженных чисел всегда получаются действительные числа:

Последнее свойство мы используем для того, чтобы ввести деление на комплексное число

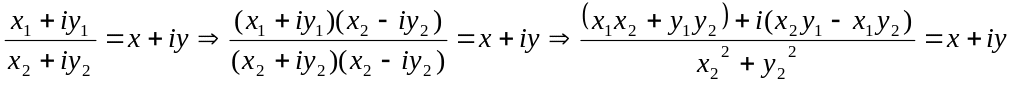
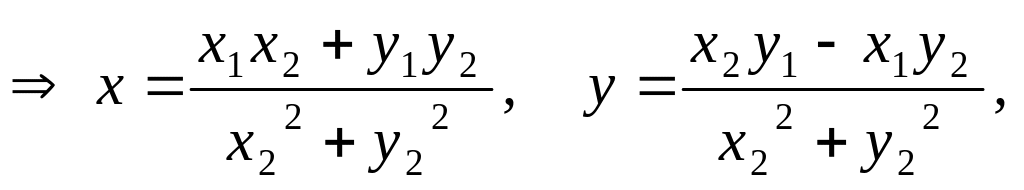
т.е.

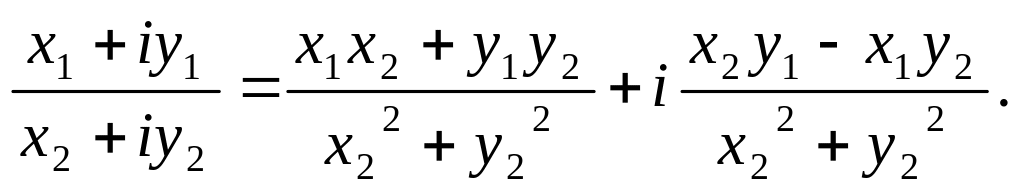
Эту формулу (как и формулу умножения) запоминать не следует. Важно понимать, как она выводится и в конкретных случаях уметь выполнять необходимые действия.

П р и м е р ы.

1. 

2. 

3. 

5.2. Запись комплексных чисел в тригонометрической и

показательной формах.

Введём понятие модуля

(5.2.1)

и аргумента комплексного числа (рис.1). Главные значения аргумента выбирают в промежутке от 0 до или от до . Аргумент комплексного числа определяется неоднозначно. Множество всех возможных значений аргумента дается формулой

Важно помнить, что

(5.2.2)

Очевидно, что

Подставляя эти выражения в (5.1.3), приходим к тригонометрической форме комплексного числа:

(5.2.3)

Докажем теорему об умножении комплексных чисел.

Теорема. При умножении комплексных чисел их модули перемножаются, а аргументы складываются.

Для доказательства удобно использовать запись комплексных чисел в тригонометрической форме:

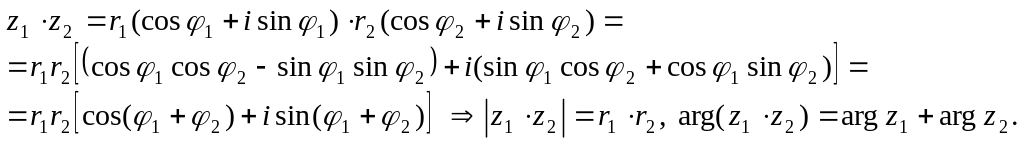При делении имеем:

Учитывая указанные свойства, Эйлер предложил записывать комплексное число в показательной форме:

(5.2.4)

При этом

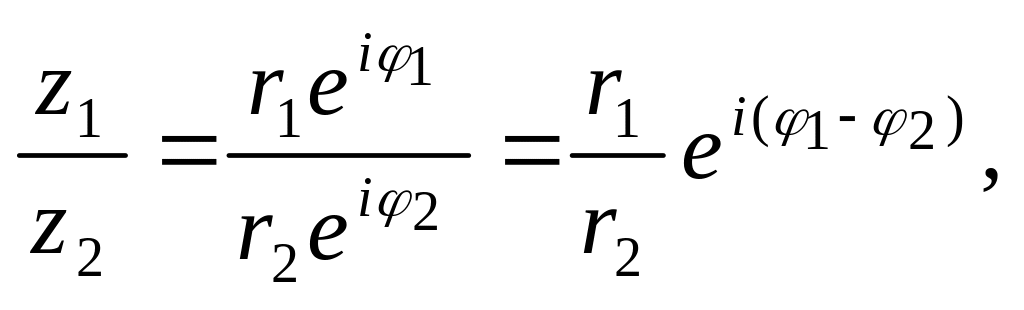
т.е. обычные законы алгебры можно распространить на степени с мнимыми показателями. Формула (5.2.4) должна быть согласована с (5.2.3):

(5.2.5)

Заменяя в (5.2.5) на получаем

(5.2.6)

Формулы (5.2.5), (5.2.6) называются формулами Эйлера.

Важно отметить, что для комплексных чисел в показательной форме справедливы не только обычные алгебраические операции, но и операции математического анализа. Так, например, при

Подобные свойства комплексных чисел будут изучаться в разделе «Теория функций комплексной переменной».