3. Дивергенция векторного поля.

ФОРМУЛА ОСТРОГРАДСКОГО

3.1. Вычисление дивергенции

Определение 3.1. Отношение потока векторного поля через поверхность к величине объема называется средней объемной плотностью потока векторного поля.

В поле скоростей жидкости это отношение при определяет среднее количество жидкости, поступающей из единицы объема внутри поверхности за единицу времени. При определяет среднее количество жидкости, поглощаемой единицей объема за единицу времени.

Определение 3.2. Дивергенцией (или расходимостью) векторного поля называется объемная

плотность потока векторного поля в этой точке:

,

где V-объем, ограниченный замкнутой поверхностью , содержащей точку М.

Если координаты вектора непрерывны вместе со своими частными производными , , , то в декартовой системе координат дивергенция вычисляется по формуле

, (3.1)

где частные производные вычислены в точке М.

Пример 3.1. Вычислить дивергенцию поля радиус-вектора .

Решение.

.

Следовательно, в каждой точке поля радиус-вектора имеется источник, плотность которого равна трем единицам.

3.2. Формула Остроградского в векторной форме

Равенство (3.1) позволяет записать формулу Остроградского в векторной форме. Если учесть, что

(3.1)

является потоком векторного поля, тогда равенство

примет следующий вид:

. (3.2)

Физический смысл формулы Остроградского заключается в том, что, если - вектор скорости жидкости, протекающей через тело ,тогда подынтегральное выражение в правой части равенства (3.2) дает полное количество жидкости ,вытекающей из тела или через поверхность за единицу времени (или втекающей в тело , если интеграл отрицателен) .Если дивергенция равна нулю , то количество жидкости , втекающей внутрь тела , равно количеству жидкости , вытекающей из него .

Формула (3.2) позволяет упростить вычисления потоков через замкнутую поверхность.

Пример 3.2. Вычислить поток поля через полную поверхность цилиндра

, .

Решение. Найдем дивергенцию

.

По формуле (3.2)

.

Перейдем к циклическим координатам, тогда .

4. Линейный интеграл в векторном поле.

ЦИРКУЛЯЦИЯ. ПЛОТНОСТЬ ЦИРКУЛЯЦИИ

4.1. Определение и вычисление циркуляции

Пусть L-пространственная кусочно-гладкая направленная линия и - непрерывное векторное поле, заданное в , где , , - проекции на координатные оси.

Определение 4.1.1. Криволинейный интеграл вида

,

взятый по некоторой направленной линии L, называется линейным интегралом от вектора вдоль линии L.

Пример 4.1. Вычислить работу силового поля

вдоль отрезка AB прямой, проходящей через точки M₁(2,3,4) и M₂(3,4,5).

Решение. Работа данного силового поля будет равна линейному интегралу вдоль отрезка M₁M₂:

.

Находим канонические уравнения прямой M₁M₂. Имеем

Отсюда

Здесь x изменяется в пределах от 2 до 3 (так как абсцисса точки M₁ равна 2, а абсцисса точки M₂ равна 3). Искомая работа будет равна

.

Определение 4.1.2. Циркуляцией векторного поля по замкнутой линии L в области называется линейный интеграл по этой замкнутой линии L, обозначаемый через Ц и определяемый формулой , где - вектор-дифференциал.

В том случае, когда - силовое поле, линейный интеграл от вектора равен работе сил поля при перемещении тока по линии L(физический смысл циркуляции).

Найдем скалярное произведение векторов и . Вектор направлен по касательной к кривой L .

.

Тогда циркуляция принимает вид

.

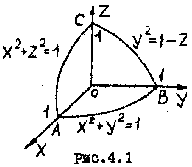
Пример 4.2. Найти циркуляцию векторного поля по контуру АВСА, полученному при пересечении параболоида с координатными плоскостями

(рис. 4.1).

Решение. .

1. Н а АВ: , ; .

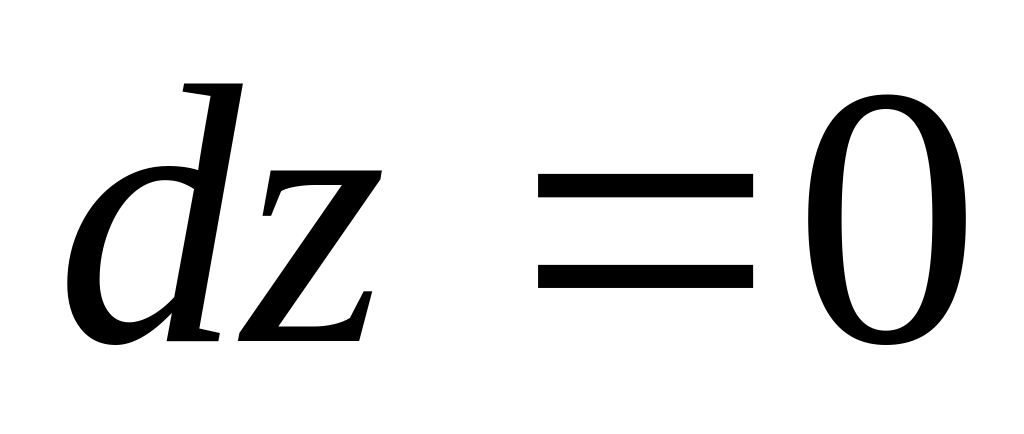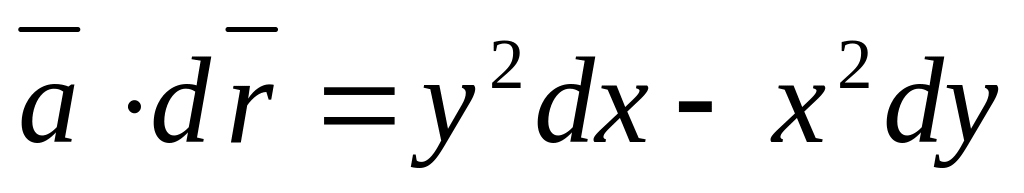Линейный интеграл

.

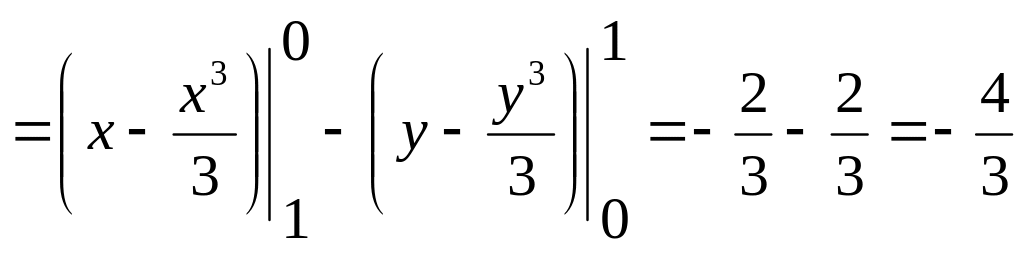2. На ВС: , ,

.

3. На СА: , ; .

Таким образом, .

Знак минус указывает на то, что под действием сил поля контур будет вращаться в отрицательном направлении, т.е. по часовой стрелке.

Пример 4.3. Вычислить циркуляцию векторного поля

вдоль линии , получаемой пересечением конуса с координатными плоскостями (рис. 4.2).

Решение. Линия состоит из двух отрезков ВС и СА, расположенных на координатных плоскостях и соответственно и

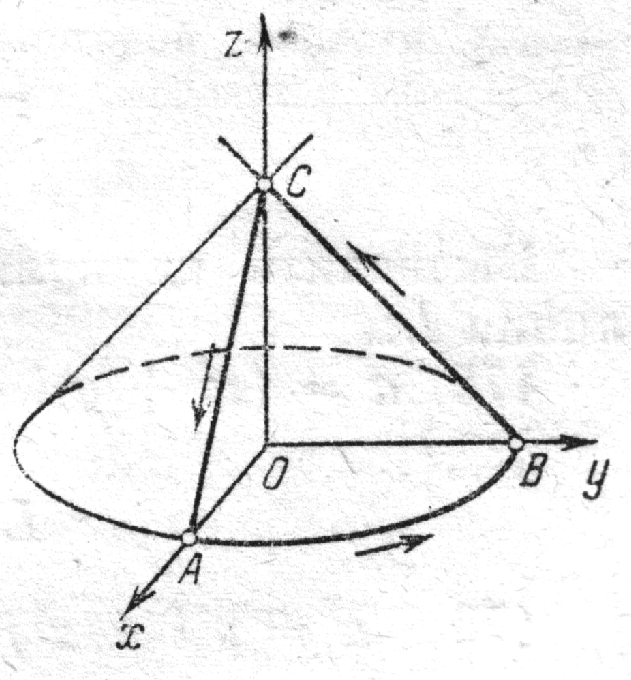дуги о кружности . Поэтому циркуляция данного векторного поля будет равна

1. На отрезке ВС имеем ,

; , ;

.

Рис. 4.2 Следовательно, .

2. На отрезке СА имеем , ; , ; .

Следовательно, .

3. На дуге окружности имеем , и значит, .

Искомая циркуляция векторного поля равна нулю.