
Идеология метода молекулярной динамики
В основе теории лежат следующие утверждения
Все процессы, происходящие в наноматериалах , в различных молекулярных системах и биологических объектах, в классических сплошных средах, в конечном счете определяются движением и взаимодействием огромного числа электронов, ионов и атомов.
Такое движение и взаимодействие определяется решением волновых уравнений Шредингера (или в более общем случае – уравнений Дирака).
Потенциал
взаимодействия между заряженными
частицами определяется только законом
Кулона.![]()
Уравнение Шредингера для системы, состоящей из ядер и электронов
![]() ,
(1)
,
(1)
![]() ,
,
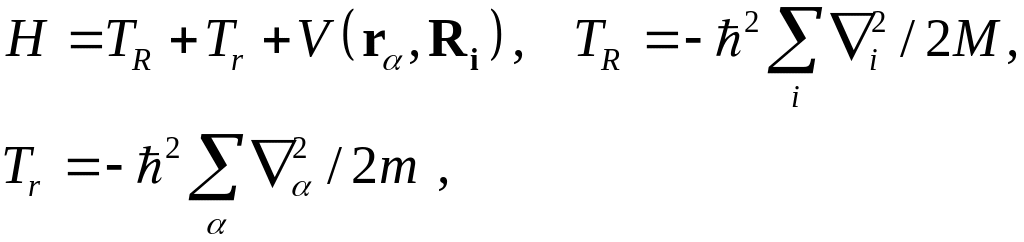 (2)
(2)
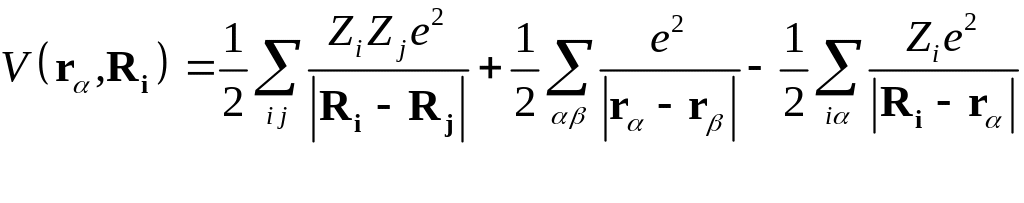 .
(3)
.
(3)
Проблема:
хотя уравнение (1) линейное,
но
функция
![]() есть функция
очень многих переменных, что
обусловливает колоссальные трудности
при его анализе и решении.
есть функция
очень многих переменных, что
обусловливает колоссальные трудности
при его анализе и решении.
Поэтому вся многочастичная теория базируется на массе предположений
относительно структуры решения, некоторые из которых даже не имеют прозрачного физического смысла.
Приближение Борна-Оппенгеймера
Приближение Борна — Оппенгеймера —метод анализа систем, заключающийся в том, что в системе выделяют и раздельно описывают ядра атомов и электроны, для которых характерные времена изменения состояния сильно различаются.
Масса ядра значительно превышает массу электрона, вследствие чего скорость движения ядер мала по отношению к скорости движения электронов. В результате медленно движущиеся ядра образуют электростатическое поле, в котором с намного большей скоростью движутся электроны, успевающие мгновенно подстроиться к любому изменению координат ядер. Поэтому в данном приближении ядра считают неподвижными или движущимися по законам классической динамики и по законам квантовой механики рассматривают только движение электронов. Это эквивалентно допущению, что полная волновая функция может быть выражена в виде произведения электронной и ядерной функций.
Имеем
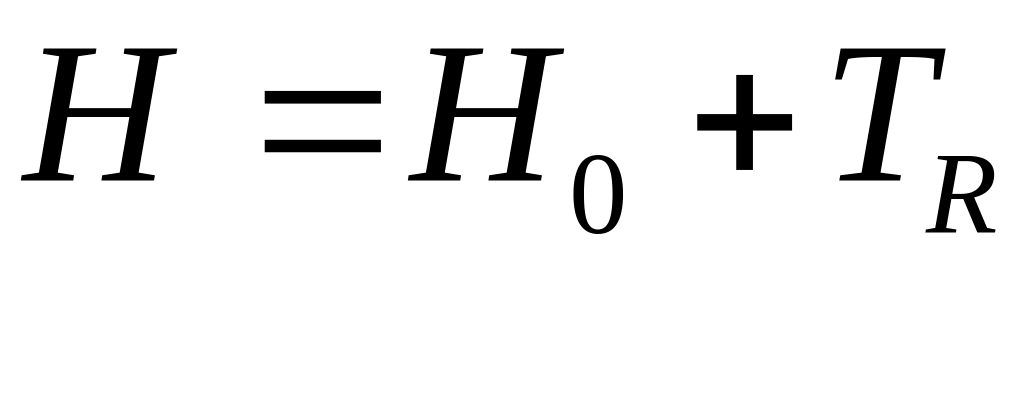 ,
(4)
,
(4)
![]() ,
(5)
,
(5)
![]() .
(6)
.
(6)
Формула
(6) – задача отыскания стационарных
состояний системы при неподвижных
ядрах.
ВФ системы в нулевом приближении
![]() и
энергии стационарных состояний
и
энергии стационарных состояний
![]() зависят от координат ядер как от
параметров.
зависят от координат ядер как от
параметров.
Для возмущенной системы
![]() .
(7)
.
(7)
Решение
(7) ищется в виде разложения по СФ оператора
![]() :
:
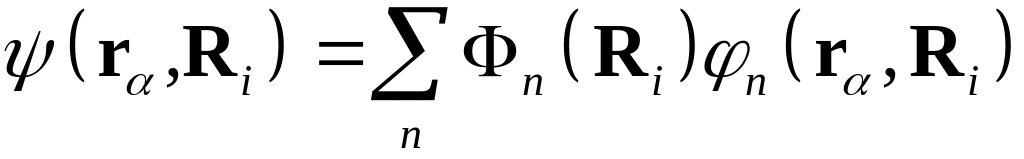 .
(8)
.
(8)
Подставляя
(8) в (7), умножая на
![]() ,
интегрируя по координатам электронов
и используя элементарную формулу
векторного анализа
,
интегрируя по координатам электронов
и используя элементарную формулу
векторного анализа
![]() ,
получим систему уравнений
,
получим систему уравнений
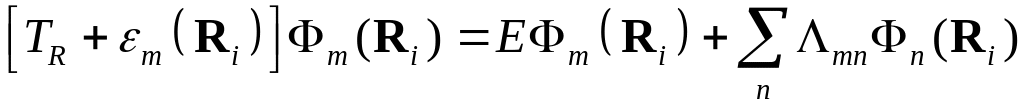 ,
(9)
,
(9)
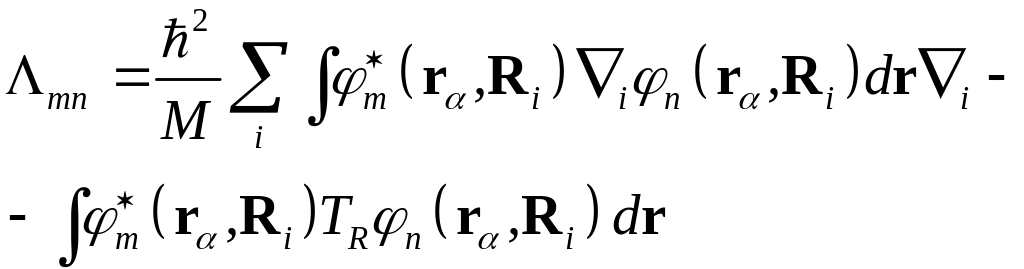 ,
(10)
,
(10)
![]() .
.
В
нулевом приближении (приближение
Борна-Оппенгеймера) оператором
![]() пренебрегают. Тогда система (9) распадается
на систему независимых уравнений
пренебрегают. Тогда система (9) распадается
на систему независимых уравнений
![]() (11)
(11)
для каждого состояния движения электронной подсистемы.
Уравнение
(11) – уравнение Шредингера с потенциальной
энергией
![]() .
Т.о., движение ядер характеризуется
потенциальной энергией
,
которая соответствует энергии электронов
при фиксированных координатах ядер.
.
Т.о., движение ядер характеризуется
потенциальной энергией
,
которая соответствует энергии электронов
при фиксированных координатах ядер.
При
переходе к классическому описанию
движения ядер энергия
будет соответствовать потенциальной
энергии межатомного взаимодействия
![]() .
.
Т.о., понятие межатомного потенциала имеет достаточно строгое квантовомеханическое обоснование в приближении Борна-Оппенгеймера.
Уравнения Хартри
В многоэлектронной системе все электроны взаимодействуют между собой, движение каждого электрона определяется движением всех остальных электронов и полем ядер. Согласно же одноэлектронному приближению, впервые предложенном Хартри, электроны движутся в определенном смысле независимо друг от друга, но движение каждого электрона определяется его волновой функцией в потенциальном поле, создаваемом ядрами и остальными электронами .
Метод самосогласованного поля — метод, в котором состояние отдельной частицы сложной системы определяется полем , создаваемым всеми остальными частицами и зависящим от состояния каждой частицы. Тем самым состояние каждой из подсистем автоматически согласуется с состояниями всех остальных частей, с чем и связано название метода.
Тогда движения электронов разделяются, и для каждого электрона может быть введена одноэлектронная функция, являющаяся решением уравнения Шредингера. Волновая функция многоэлектронной системы представляется в виде произведения одноэлектронных функций (орбиталей)
![]() (12)
(12)
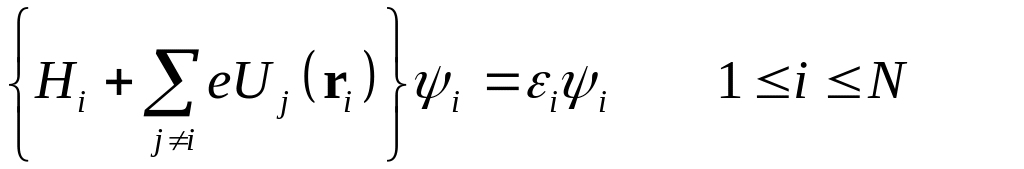 (13)
(13)
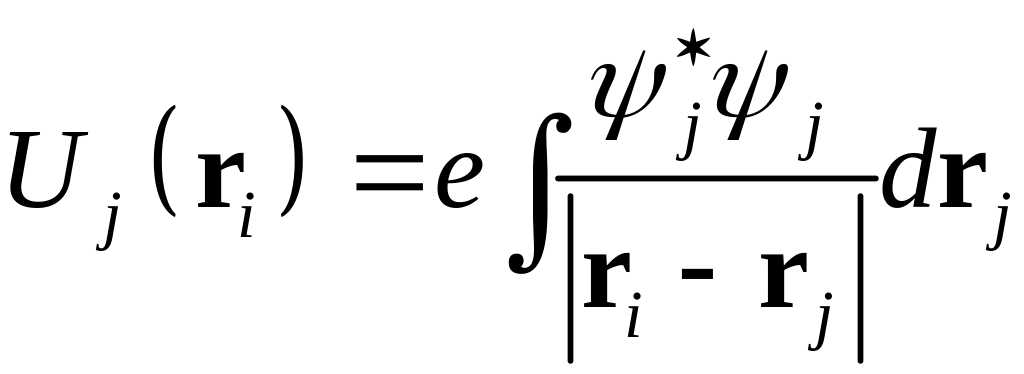 -
(14)
-
(14)
потенциал,
создаваемый электроном
![]() в точке
в точке
![]() ,
или в эквивалентной форме
,
или в эквивалентной форме
![]()
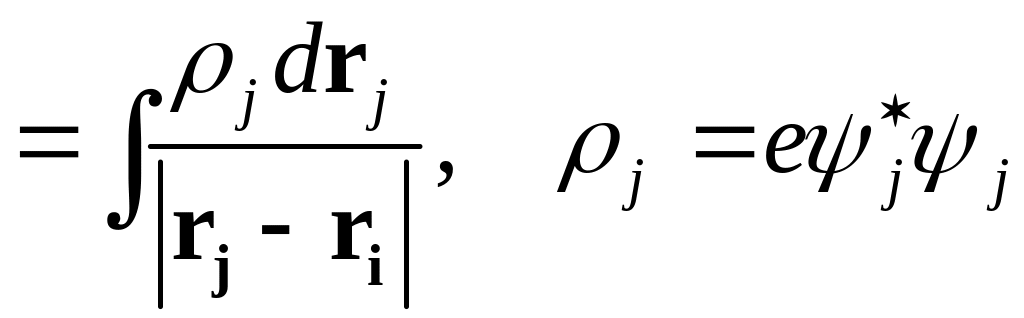 (15)
(15)
Оператор Гамильтона, действующий на каждую электронную волновую функцию, зависит от состояния всех остальных электронов системы.
Ф. (15) есть решение уравнения Пуассона
![]() .
(16)
.
(16)
Система уравнений Хартри окончательно имеет вид
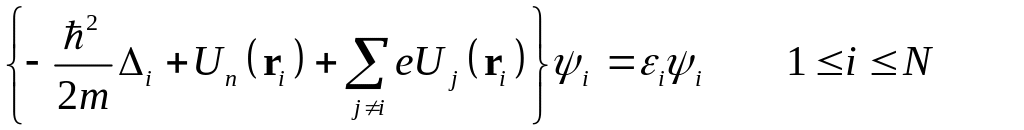 ,
(17)
,
(17)
![]() .
(18)
.
(18)
Уравнения Хартри-Фока
Правильная запись волновой функции для двух электронов
 (19)
(19)
Обобщение
на систему
![]() неразличимых фермионов
неразличимых фермионов
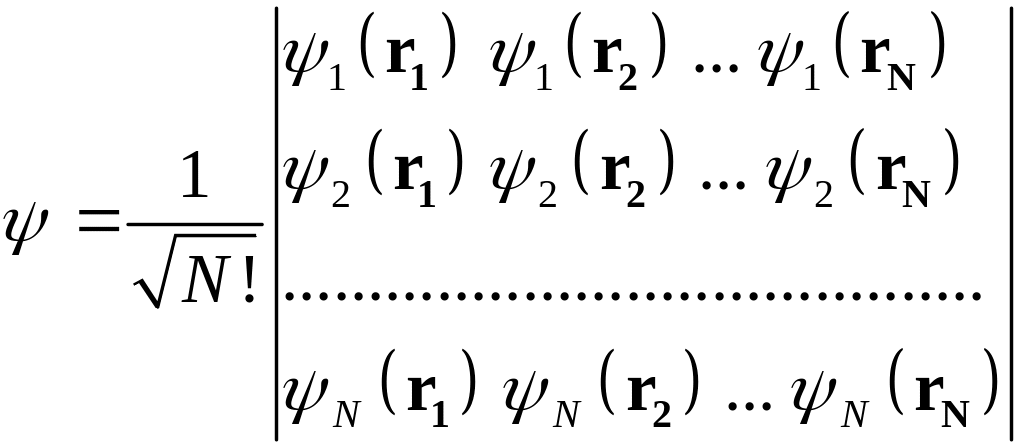 .
(20)
.
(20)
Не может быть двух одинаковых одночастичных волновых функций.
С помощью (20) вместо уравнений Хартри можно получить
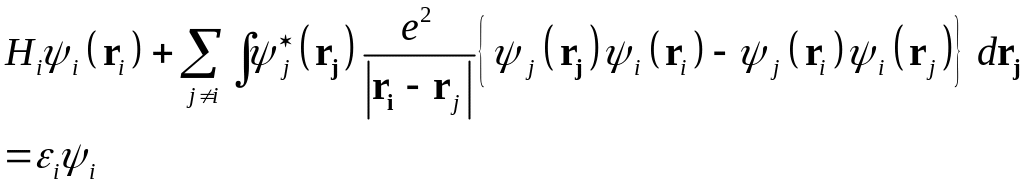 (21)
(21)
Система уравнений для одноэлектронных состояний называется системой уравнений Хартри-Фока. Перепишем ее в виде
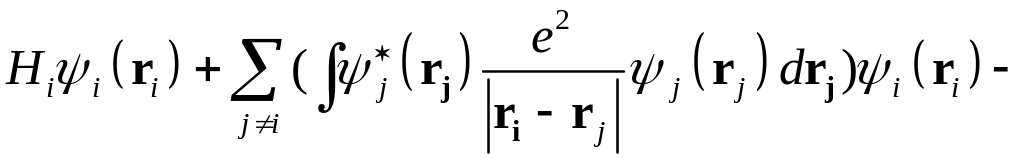
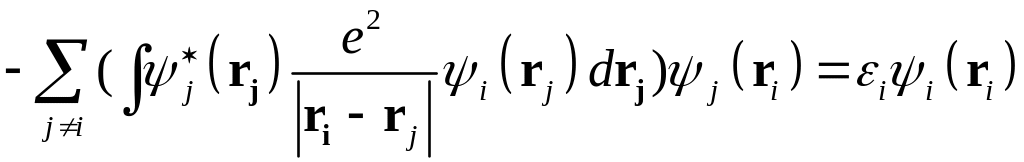 .
(22)
.
(22)
Вторая сумма определяет т.н. обменный потенциал. Выразим интегралы через потенциалы частиц, удовлетворяющие уравнениям Пуассона
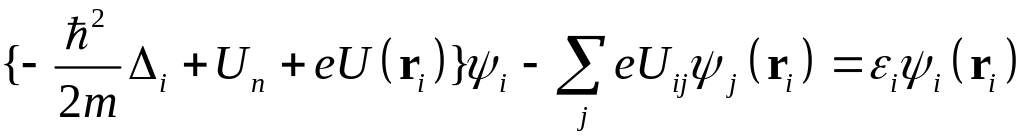 .
(22)
.
(22)
Уравнение
для полного потенциала, создаваемого
всеми электронами кроме
![]() -того,
в точке нахождения
-того
электрона
-того,
в точке нахождения
-того
электрона
 ,
(23)
,
(23)
 .
(24)
.
(24)
Уравнения для обменных потенциалов
![]() ,
(25)
,
(25)
 .
(26)
.
(26)
