Доказательство.
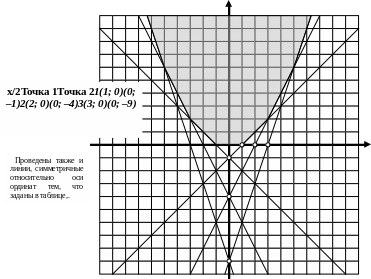
П рямая QT использовалась нами при построении точки Т, лежащей на параболе у = ах2. Если тщательно выполнить чертеж, то можно догадаться о том, что она касается параболы. Но эта догадка будет оставаться только догадкой, пока не будет проведено доказательство.
Подстановкой координат легко убедиться, что уравнение прямой QT имеет вид:
у = 2а х0 х – ах02.
Важно отдавать себе отчет в том, что величины х и у в уравнении являются переменными, а х0 и а – постоянными. Рассмотрим любую, лежащую на одной вертикали, пару точек параболы и прямой QT (они имеют одинаковые абсциссы). Найдем разность их ординат:
ах2 – (2а х0 х – ах02) = ах2 – 2а х0 х + ах02 = а(х – х0)2.

Определение. Пусть на плоскости задано бесконечное семейство прямых. Если существует кривая, касающаяся каждой из этих прямых, она называется огибающей семейства.
Следствие из теоремы 3. Огибающей семейства прямых, проходящих через точки ( ; 0) и (0; – ах2) при всевозможных значениях х, является парабола у = ах2. Действительно, подставив в уравнение касательной значение х = 0, установим, что касательная к параболе проходит не только через точку ( ; 0), но и через точку (0; – ах2).
Мы получили новый способ, с помощью которого можно получить представление о форме кривой. Если график строится по точкам, то наш способ очерчивает контуры кривой с помощью прямых.
Задание. С помощью огибающих построить на клетчатой бумаге очертания параболы у = 0,25х2.
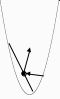 В
механике и оптике касательные к кривым
играют особую роль. Начнем с механики.
Если тело движется по кривой, то постоянно
меняет направление. Как узнать, куда
направлена скорость в данное мгновение?
Ответ таков: она направлена по касательной.
Перейдем к оптике. Луч света падает на
кривое, а не на плоское зеркало. Куда
пойдет отраженный луч? Ответить на этот
вопрос помогает следующий закон оптики:
угол падения равен углу отражения.
Но как измерить угол между прямым лучом
и искривленной поверхностью? Ответ
снова связан с касательной. Для
искривленных зеркал углы падения и
отражения измеряются по отношению к
касательной. Если в дальнейшем мы
столкнемся с движением точки по параболе
или с параболическим зеркалом, то теорема
3 поможет нам разобраться с проблемами
механики и оптики. Именно по этой причине
мы и в дальнейшем будем проявлять особый
интерес к касательным.
В
механике и оптике касательные к кривым
играют особую роль. Начнем с механики.
Если тело движется по кривой, то постоянно
меняет направление. Как узнать, куда
направлена скорость в данное мгновение?
Ответ таков: она направлена по касательной.
Перейдем к оптике. Луч света падает на
кривое, а не на плоское зеркало. Куда
пойдет отраженный луч? Ответить на этот
вопрос помогает следующий закон оптики:
угол падения равен углу отражения.
Но как измерить угол между прямым лучом
и искривленной поверхностью? Ответ
снова связан с касательной. Для
искривленных зеркал углы падения и
отражения измеряются по отношению к
касательной. Если в дальнейшем мы
столкнемся с движением точки по параболе
или с параболическим зеркалом, то теорема
3 поможет нам разобраться с проблемами
механики и оптики. Именно по этой причине
мы и в дальнейшем будем проявлять особый
интерес к касательным.
М
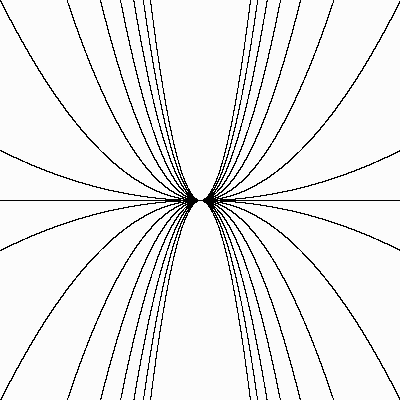
Мы уже достаточно хорошо представляем себе форму параболы. Она похожа на чашу с выпуклым дном. Нижняя точка этой чаши (или верхняя, если чашу перевернуть) называется вершиной параболы1. Все параболы вида у = ах2 при любых значениях а имеют вершину в начале координат. Все они являются результатом сжатия (при а < 1) или растяжения (при а > 1) параболы у=х2. При а > 0 ветви параболы смотрят вверх, при а < 1 – вниз, при a = 0 парабола вырождается в прямую у = 0.
Если сместить вершину параболы в точку (х0; у0), то она не изменит формы, но будет описываться другим уравнением. Преобразование уравнения параболы состоит в том, у заменяется на у – у0, а х – на х – х0. В итоге мы приходим к уравнению
у – у0 = а(х – х0)2.
Раскроем скобки и явно выразим у через х. Как результат будет получено уравнение
у = ах2 – 2ах0х + ах02 + у0.
Для краткости принято обозначать коэффициент при х через b, а свободный член – через с, то есть
b = – 2ах0 ; с = ах02 + у0.
Итоговое уравнение параболы со сдвинутой из начала координат вершиной таково:
у = ах2 + bх + c.
Мы видим, что в этом случае парабола является графиком квадратного трехчлена, теснейшим образом связанного с квадратными уравнениями.
Выразим х0 и у0 через а, b и с:
b = – 2ах0 с = ах02 + у0
![]()

![]()
Теперь у нас есть повод и возможность вспомнить о том, как решаются квадратные уравнения. Это тем более уместно, что многие задачи, решаемые методом координат, приводят именно к квадратным уравнениям.
Перепишем наше исходное уравнение у – у0 = а(х – х0)2, используя полученные выше формулы
![]() .
.
Положив у = 0, получим:
![]() .
.
Откуда вытекает известная формула для решения квадратного уравнения:
![]() .
.
Эта формула показывает, что квадратное уравнение может иметь два решения (при дискриминанте b2 – 4ac > 0), одно решение (при дискриминанте равном 0), нe иметь решений (при дискриминанте меньше 0). C геометрической точки зрения эти cлучаи соответствуют различным положениям параболы относительно оси абсцисс.
|
|
|
Парабола пересекается с осью абсцисс в двух точках – два решения. |
Парабола касается оси абсцисс в единственной точке – одно решение. |
Парабола не пересекается с осью абсцисс – нет решений. |
Задача. Докажите, что если в фокусе параболы разместить источник света, то лучи, отраженные от параболы, будут направлены параллельно друг другу и перпендикулярно директрисе. (Именно по этой причине прожектора имеют параболические отражатели).