О параболе.

(14)

Определение. Кривая, уравнение которой в некоторой системе координат можно записать в виде

у = ах²

называется параболой.

В алгебре начинают изучать форму кривых, представляющих собой графики функций, следующим образом. В таблице задают значения независимой переменной х, по ним вычисляют значения переменной у и по точкам строят график. Но мы постараемся с самого начала использовать геометрические способы исследования. В этом нам поможет следующая простая теорема.

Теорема 1. Пусть два прямоугольных треугольника АСВ и А₁С₁В₁ подобны. Кроме того, пусть АС = , а ВС = А₁С₁ = . Тогда В₁С₁ = ах².

Доказательство.

Из подобия треугольников следует, что АС : ВС = А₁С₁ : В₁С₁. Или В₁С₁. Из пропорции следует, что В₁С₁ = , и, наконец, требуемое равенство: В₁С₁ = ах².

Этой простой теоремой можно воспользоваться весьма успешно. Вся хитрость будет заключаться в том, чтобы правильно расположить треугольники АСВ и А₁С₁В₁ относительно друг друга и системы координат. Но прежде чем приступить к этому, отметим, что согласно традиции буква а обозначает постоянную величину, а х – переменную. И, действительно, в дальнейшем катет АС будет иметь постоянную длину, а остальные катеты – переменную.

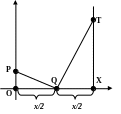Используя теорему 1, мы сможем построить любую точку параболы без вычислений и таблиц. Для этого зафиксируем на координатной плоскости точку Р (0; ). Затем, выбрав произвольное значение х, зададим точки Q ( ; 0) и X (х; 0).

Первый треугольник РОQ уже начерчен. Далее через точку Х проведем вертикальную прямую, а через точку Q до пересечения с этой вертикалью в точке Т прямую QТ, перпендикулярную к прямой РQ. Прямоугольные треугольники РОQ и QХТ подобны, поскольку РQО = QТХ, как углы с соответственно перпендикулярными сторонами.

Мы можем использовать теорему 1. Длина отрезка ХТ равна ах², следовательно точка Т лежит на параболе у = ах².

Теорема 2. Любая точка, лежащая на параболе у = ах², равноудалена от точки Р (0; ), называемой фокусом параболы, и прямой у = – , называемой директрисой параболы.

Доказательство.

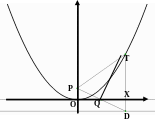
Наше доказательство основывается на на предыдущей конструкции и даже не-сколько упрощает построение точки Т. На координатной плoскости выделим фокус Р и проведем директрису параболы. Выберем на оси абсцисс произвольную точку Х и проведем через нее вертикальную прямую до пересечения с директрисой в точке D.

Соединим точки Р и D отрезком. Он пересечет ось абсцисс в точке Q, являющейся серединой отрезка OX. Действительно, прямоугольные треугольники РQO и DQX равны, поскольку РО = ХD (по способу построения фокуса и директрисы) и РQO = DQX (как вертикальные углы). Мы установили не только, что ОQ = QX, но и что РQ = QD.

Через точку Q проведем перпендикуляр к отрезку РD до пересечения с вертикалью ХD в точке Т. Эта точка, как доказано выше, лежит на параболе. Треугольники РQТ и DQТ являются прямоугольными. Катет QТ у них общий и РQ = QD. Значит, трeугольники равны, и, кроме того равны их гипотенузы РТ и ТD. Но длина отрезка РТ равна расстоянию от точки Т, лежащей на параболе, до фокуса Р, а ТD – перпендикуляр, опущенный на директрису, и его длина равна расстоянию от Р до директрисы. Теорема доказана.

Обычно параболу определяют геометрически, как геометрическое место точек, равноудаленных от точки и прямой. Но мы поступили иначе, получив основное свойство параболы с помощью ее уравнения у = ах².

На примере параболы отметим один важный момент, связанный с уравнениями различных линий в прямоугольной системе координат. Ее уравнение задает функцию, поскольку каждому значению переменной х соответствует единственное значение переменной у. Парабола является графиком этой функции, определенным образом расположенным по отношению к осям системы координат. Однако, если рассматривать параболу как геометрический объект, она может располагаться по отношению к осям произвольным образом. Она перестает быть графиком какой-либо функции, и ее уравнение усложняется. То же самое происходит и с эллипсами.

По этой причине мы всегда будем так выбирать систему координат, чтобы уравнения линий были наиболее простыми. Но из этого не следует делать вывод, что наклоненные по отношению к осям координат параболы и эллипсы в таком положении не имеют уравнений. Такие уравнения существуют, но для нас они слишком сложны.

К тому же в удачно выбранной системе координат удобнее изучать свойства различных линий. Сейчас мы продолжим этим заниматься.

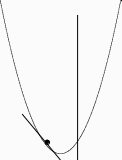
Касательную к окружности и эллипсу можно определить как прямую, имеющую с соответствующей кривой единственную общую точку. Подходит ли для касательной к параболе такое же определение: касательной к параболе называется прямая, имеющая с ней только одну общую точку? На чертеже мы видим, что это не так. Любая вертикальная прямая имеет с параболой только одну общую точку, но она не касается параболы (касаться – значит поглаживать, скользить вдоль), а буквально протыкает ее. Парабола делит плоскость на две бесконечных области. Протыкающая параболу прямая из одной области попадает в другую, касающаяся ее –лежит в одной области. Можно сказать и иначе: парабола лежит по одну сторону от касающейся ее прямой. Именно это обстоятельство и нужно отразить в определении параболы.

Определение. Касательной к параболе называется прямая, имеющая с ней только одну общую точку, и такая, что парабола лежит по одну сторону от этой прямой.

Теорема 3. Прямая QT, проходящая через точки Q ( ; 0) и Т (х₀; ах₀²) является касательной к параболе у = ах².