Точки разрыва функции
Пусть
функция
определена
в точках некоторой окрестности точки
,
кроме, быть может, самой точки 
Определение.
Точка а называется точкой разрыва
функции
,
если не выполнено равенство
(то
есть функция не является непрерывной
в точке 
).
Если
а – точка разрыва и существуют конечные
пределы
и
,
то а называется точкой разрыва первого
рода. Если при этом
,
то а называется точкой устранимого
разрыва. На рис. 2 в точках 
функция имеет разрыв первого рода, при
этом точка 
устранимая, а 
- точка скачка.
Точки
разрыва функции
,
не являющиеся точками разрыва первого
рода, называются точками разрыва второго
рода. Если при этом
или
,
то а называется точкой бесконечного
разрыва. В точках
на рис.2 и рис.3 функции имеют разрыв
второго рода (в обоих случаях бесконечный).
Заметим, что на рис.3 изображён график
Если
в полуокрестности слева или справа от
а
не определена, то для исследования
характера разрыва рассматривают только
или
.
Следовательно,
на рис. 2 
является устранимой, 
- точка непрерывности, на рис. 3 
- устранимая.
Более
сложные, чем мы рассмотрели, случаи
разрыва второго рода дают функции 
, Дирихле и Римана [1,2].
y
y
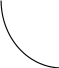
0
1
x
e
d
0
c
a
b
x
Рис.2 Рис.3
Пример
41.
Найти точки разрыва функции
и исследовать их характер.
Решение.
В точках
функция непрерывна, поскольку является
произведением или частным непрерывных
функций. В точке
оба односторонних предела существуют
и не равны:
.
Следовательно,
- точка разрыва первого рода. В точке
х=1
,
следовательно,
- точка разрыва второго рода
( точка бесконечного разрыва).
Пример
42.
Определить точки разрыва функции
и исследовать их характер.
Решение.
Находим область определения
функции:
Отсюда
или
. На
функция непрерывна: на множестве
в силу арифметических свойств и
непрерывности корня, а в точках
- поскольку они являются изолированными
(отдельными) точками
.
Таким образом, точками разрыва могут
быть только
.
Находим
.
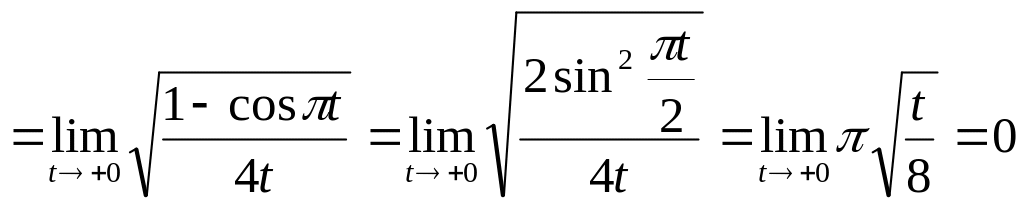Поскольку
чётная,
то и
.
Следовательно,
- точки устранимого разрыва.
Пример
43.
Исследовать на непрерывность функцию
и построить её график.
Решение.
Пусть х>0. При х>1
и у=0. При
у=1. При
и
Таким образом, при
(одновременно
строим график, рис.4);
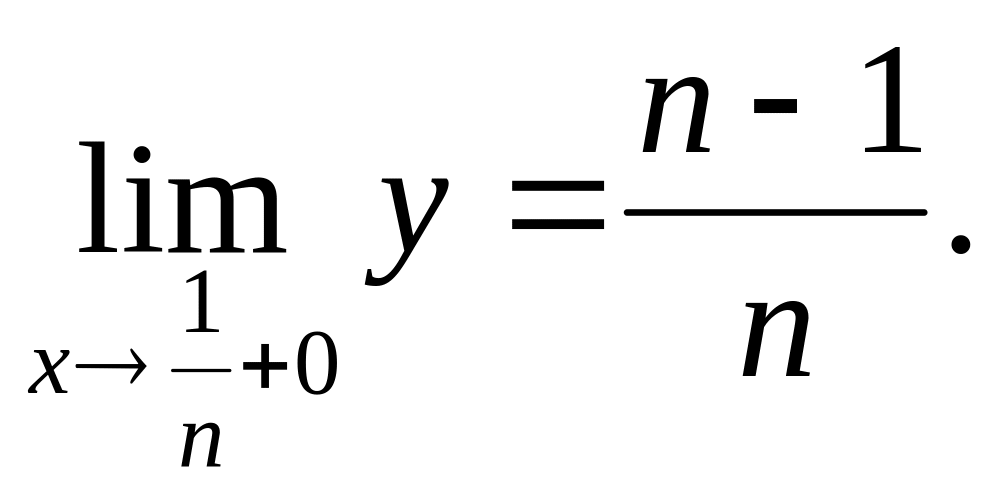Следовательно,
,
являются для у точками разрыва первого
рода. Пусть теперь х<0. При х < -1
и
.
При
,
у=1. При
и
Таким образом, при
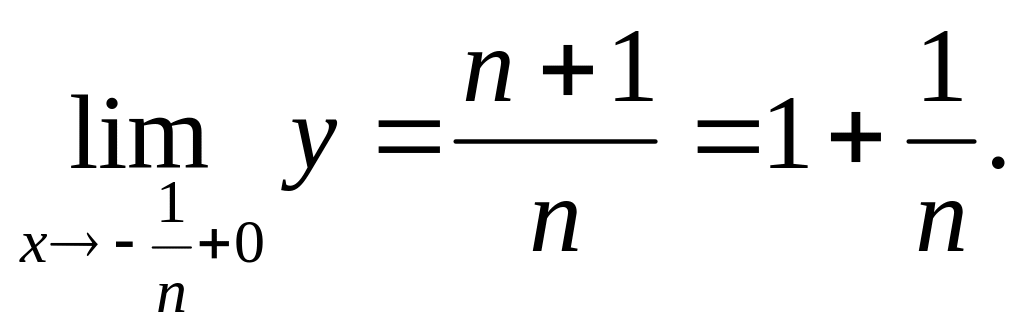
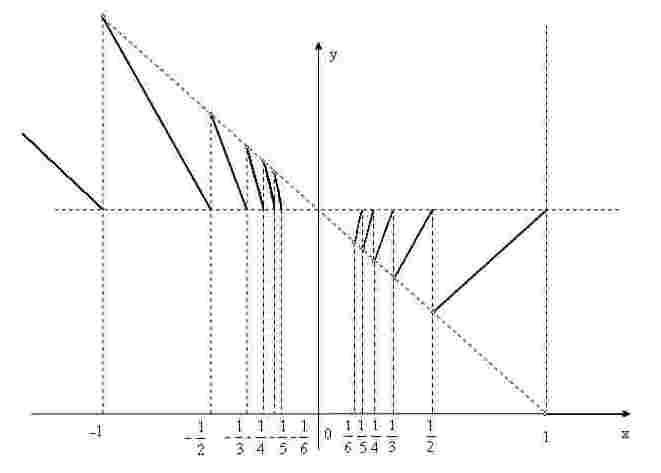
Рис. 4
Получаем,
что и точки
,
являются точками разрыва первого рода.
Поскольку
то х=0 является точкой устранимого
разрыва. Во всех остальных точках функция
непрерывна.
Ответ:
- точки разрыва первого рода, 
- точка устранимого разрыва.
Л И Т Е Р А Т У Р А
Демидович Б.П. Сборник задач и упражнений по математическому анализу: Учеб.пособие для вузов.- М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2002.- 558 с.
Ляшко И.И., Боярчук А.А., Гай Я.Г., Головач Г.П. Математический анализ в примерах и задачах, ч.1. Введение в анализ, производная, интеграл. – Киев, Издательское объединение «Вища школа», 1974.-680 с.
Кузнецов Л.А. Сборник задач по высшей математике. Типовые расчёты: Учебное пособие. 3-е изд., испр.-СПб.: Издательство «Лань», 2005. -240 с.
Кузнецова М.Г. Типовой расчёт по высшей математике: Пределы.- Ульяновск: УлПИ, 1987.- 24 с.
Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум – М.: Издательство Юрайт; Высшее образование, 2010. – 909с.