
- •Методы Оптимизации
- •1) Общая постановка задачи математического программирования.
- •2) Метод неопределенных множителей Лагранжа при поиске максимальных значений функций.
- •3) Линейный функционал.
- •4) Понятие вариации функционала.
- •5) Вычисление вариации функционала.
- •6) Постановка задачи Эйлера.
- •7) Уравнение Эйлера.
- •8) Пример использования уравнения Эйлера для поиска оптимального управления.
- •9) Понятие близости кривых.
- •10) Уравнение Эйлера-Пуассона.
- •11) Пример использования уравнения Эйлера-Пуассона в теории оптимального управления.
- •12) Вариационные задачи с подвижными границами. Пример в теории управления.
- •13) Вариационные задачи на условный экстремум.
- •14) Множители Лагранжа в вариационном исчислении.
- •15) Пример использования множителей Лагранжа для поиска управлений.
- •16) Понятие переменных состояния.
- •17) Постановка задачи оптимального управления.
- •18) Линеаризация дифференциальных уравнений и ее использование при получении принципа максимума.
- •19) Принцип максимума.
- •20) Теорема о числе переключений.
- •21) Определение моментов переключения.
- •22) Принцип оптимальности.
- •23) Дискретная форма динамического программирования.
- •24) Учет ограничений в методе динамического программирования.
- •25) Постановка задачи линейного программирования.
- •26) Определение моментов переключения.
- •27) Симплексный метод.
- •28) Геометрическая интерпретация симплексного метода.
- •29) Учет ограничений типа неравенств в линейном программировании.
- •Дополнительные материалы
19) Принцип максимума.
Пусть объект
управления описывается системой
уравнений
 .или
в векторной форме
.или
в векторной форме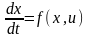 ,где
,где
 -вектор
координат состояния,
-вектор
координат состояния, -вектор
координат управления. Основная задача
оптимального управления: среди всех
допустимых управлений, переводящих
динам. Сис-му из начального положения
x0 в конечное x1,
найти оптимальное. Для определения
критерия оптимальности рассмотрим
функционал
-вектор
координат управления. Основная задача
оптимального управления: среди всех
допустимых управлений, переводящих
динам. Сис-му из начального положения
x0 в конечное x1,
найти оптимальное. Для определения
критерия оптимальности рассмотрим
функционал
 .Он
должен достигать минимума.
.Он
должен достигать минимума.
Принцип
максимума Понтрягина основан на
установлении связи оптимизируемого
функционала J с динамикой
процесса. Эта связь устанавливается
через функцию Гамильтона
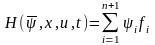 ,где
,где
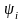 удовлетворяет уравнениям
удовлетворяет уравнениям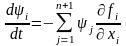 ,j=0,1,..,n.
Принцип максимума Понтрягина состоит
в том, что для оптимального управления
и соответствующих координат
,j=0,1,..,n.
Принцип максимума Понтрягина состоит
в том, что для оптимального управления
и соответствующих координат
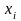 ,для
которых критерий J имеет
минимальное значение, функция Гамильтона
H имеет максимум(по
аргументу U).
,для
которых критерий J имеет
минимальное значение, функция Гамильтона
H имеет максимум(по
аргументу U).
Функции H(y,
x, и) ставится в соответствие каноническая
(гамильтонова) система (относительно
y, х)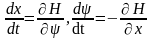 .
.
20) Теорема о числе переключений.
(Следствие принципа максимума)
(Для уст. Систем)
Для того, чтобы линейная динамическая система порядка n, имеющей различные не положительные корни характеристического уравнения, перевести за минимальное время из одного состояния в другое, требуется не более n интервалов управления (не более n-1 переключения)
Причём на каждом из интервалов управляющее воздействие равно либо +Umax , либо -Umax
21) Определение моментов переключения.
1. U(t) – задаётся явная зависимость от времени
2. U – задаётся как ф-ия переменных состояние U(x1…xn)
Рассмотрим схему
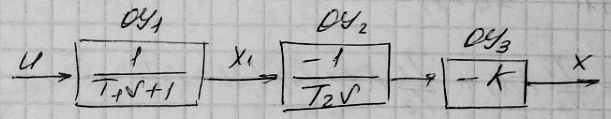
Требуется перевести систему из одного состояния в другое за минимальное время.
Св-ва управляющего воздействия
1.U(t) либо +Uм либо –Uм
2. Имеются 2а интервала управления.
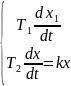
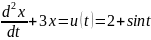
Можно решить методом фазовой плоскости?
F(X,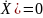
F(X,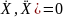

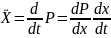 =
=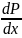 p;
F(x,P,
p;
F(x,P,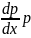 )=0
)=0
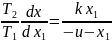
x=c-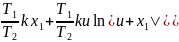
x=0, x1=0, ->c=0
x=-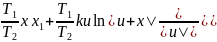
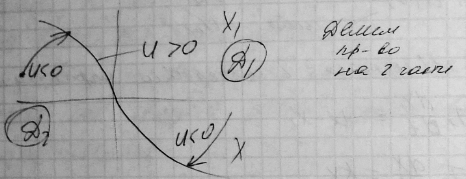
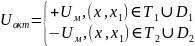
22) Принцип оптимальности.
Каждый конечный участок оптимальной траектории есть оптимальная траектория (следствие аддитивности).
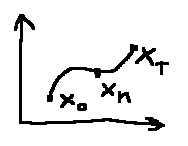
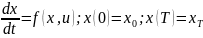
Принцип оптимальности (применения) – перевести систему из одного состояния в другое на интервале времени [0, T]. Критерий:
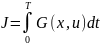
23) Дискретная форма динамического программирования.
 Переход к дискретной системе : рассмотрим
U,x в отдельных
точках.
Переход к дискретной системе : рассмотрим
U,x в отдельных
точках.
Будем искать приближенное значение U,x на интервалах
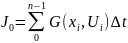 ,
,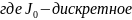
Рассм.
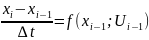 – дифур. стало разностным уравнением
– дифур. стало разностным уравнением
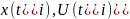 – дискретная задача
– дискретная задача
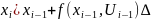 – ограничение
– ограничение
Метод динамического программирования – метод поиска наибольшего/наименьшего значения ф-ции многих переменных при наличии ограничения на переменные, ограничения в виде разностных уравнений.
Если ограничение общего вида, то этот метод не подходит.
Вместо сложной задачи решаем много простых задач поиска наиб./наим. значения ф-ции одного аргумента.Например необходимо найти методом градиента наиб./наим. значение.Задача общая, общего решения нет … Наш метод опред. решение.
Решение задачи начинается с конца траектории (с конечной точки )
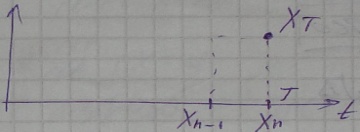 Решение основано на принципе оптимальности
Решение основано на принципе оптимальности
Шаг 1 для
 . Пусть
-
известно. Тогда
. Пусть
-
известно. Тогда
 - разностное уравнение. Для каждого
находим оптимальное значение
- разностное уравнение. Для каждого
находим оптимальное значение
 .
.
Уравнение
становится относительно корней -
необходимо выбрать оптимальное уравнение:
-
необходимо выбрать оптимальное уравнение:
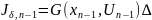
Итоги шагов: Шаг 1 для
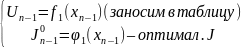
Шаг 2 для
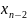 .
Пусть
.
Пусть
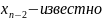 .Тогда
.Тогда
 .
.
Дискретный
критерий
 начиная с
движемся оптимально
начиная с
движемся оптимально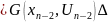 +
+
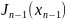 .Из 4-ёх аргументов получили 3.
.Из 4-ёх аргументов получили 3.
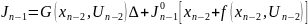
Шаг 2 для
.
ИТОГ: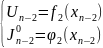
Далее доходим
до шага, где
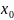 -известно,
потом пойдем в обратном направлении
-известно,
потом пойдем в обратном направлении
ПРИМЕР:
10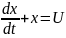 x(0) =1, x(T)
=10 T=3
x(0) =1, x(T)
=10 T=3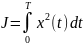
Оптимальным
способом перевести систему из нач. сост.
в конечное за 3 секунды, чтобы критерий
принял минимальное значение. Принять
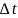 =1.
Разностное уравнение:
=1.
Разностное уравнение:

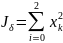
Шаг 1. Для
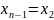 .
Пусть
.
Пусть
 .
Разн. уравнение:
.
Разн. уравнение:
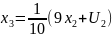 ,
,
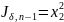 . Найти оптимальное управляющее
воздействие:
. Найти оптимальное управляющее
воздействие:
x(T)
=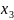 =10
=10
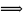
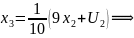
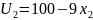 Итог:
Итог:

Шаг 2. Для
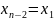 .
Пусть
.
Пусть
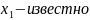 .
Разн. уравнение:
.
Разн. уравнение:
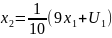 ,
,
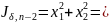 начиная с
движение
оптимально =
начиная с
движение
оптимально =
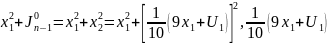 -приравниваем
к 0
-приравниваем
к 0
Итог :
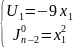
Шаг 3. Для
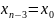 .
Пусть
.
Пусть
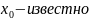 .
Разн. уравнение:
.
Разн. уравнение:
 ,
,
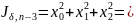 начиная с
движение
оптимально =
начиная с
движение
оптимально =
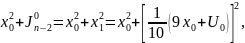 Ищем
оптим.
Ищем
оптим.
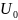 для каждого
для каждого
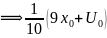 -приравниваем
к 0
.
Итог :
-приравниваем
к 0
.
Итог :
Движемся в
обратную сторону:
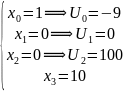
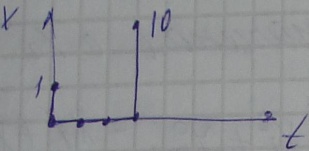
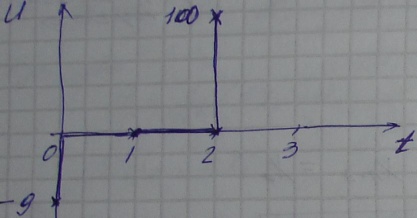
Для
непрерывных систем :
 -
-
Для диф-я 2-го порядка решение усложняется. Метод динамического программирования применим в комбинаторных задачах.
