
- •Методы Оптимизации
- •1) Общая постановка задачи математического программирования.
- •2) Метод неопределенных множителей Лагранжа при поиске максимальных значений функций.
- •3) Линейный функционал.
- •4) Понятие вариации функционала.
- •5) Вычисление вариации функционала.
- •6) Постановка задачи Эйлера.
- •7) Уравнение Эйлера.
- •8) Пример использования уравнения Эйлера для поиска оптимального управления.
- •9) Понятие близости кривых.
- •10) Уравнение Эйлера-Пуассона.
- •11) Пример использования уравнения Эйлера-Пуассона в теории оптимального управления.
- •12) Вариационные задачи с подвижными границами. Пример в теории управления.
- •13) Вариационные задачи на условный экстремум.
- •14) Множители Лагранжа в вариационном исчислении.
- •15) Пример использования множителей Лагранжа для поиска управлений.
- •16) Понятие переменных состояния.
- •17) Постановка задачи оптимального управления.
- •18) Линеаризация дифференциальных уравнений и ее использование при получении принципа максимума.
- •19) Принцип максимума.
- •20) Теорема о числе переключений.
- •21) Определение моментов переключения.
- •22) Принцип оптимальности.
- •23) Дискретная форма динамического программирования.
- •24) Учет ограничений в методе динамического программирования.
- •25) Постановка задачи линейного программирования.
- •26) Определение моментов переключения.
- •27) Симплексный метод.
- •28) Геометрическая интерпретация симплексного метода.
- •29) Учет ограничений типа неравенств в линейном программировании.
- •Дополнительные материалы
17) Постановка задачи оптимального управления.
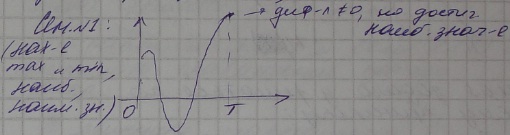
dxi/dt = fi ( x1…,xn,u(t),t) , i=1,..,n; x(0)=M0 ; x(T)=MT
Требуется перевести динамическую систему из одного состояния в другое оптимальным образом, для определения критерия оптимальности рассмотрим функционал:
J=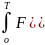 1,..,xn
,x1/,..,xn/(t),u(t))dt
1,..,xn
,x1/,..,xn/(t),u(t))dt
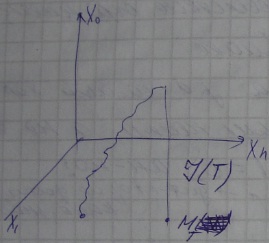
Управляющее воздействие ограничено: |u(t)| ≤ umax
Значение функционала должно быть самым хорошим, т.е. наиб. или наим., а не то, где вариация = 0, аналогично:
Вводится вспомогательная переменная X0(t), dX0(t)/dt =F(t,X1,..,Xn/,U);
X0(t)= => X0(0)=0,
т.е. мы формируем нач. условие X0(t)=J
=> X0(0)=0,
т.е. мы формируем нач. условие X0(t)=J
После ввода переменной получаем систему дифф. ур-ий:
dxi*/dt =fi( ), i=0,1…, n
x*=
Т.е. м. избавиться от t
Такая задача должна решаться по общему принципу:
если приращение ф-ла ’’-’’, то достигается наиб. знач.
Вводится понятие :
Игольчатая вариация - очень узкий импульс, площадь д.б. конечной, чтобы система могла сдвинуться с места (τ мало).

Необх. решать с-му уравнений…
Движение будет оптимальным, если X0(t) б. принимать приращение одного знака.
В принципе максимума б. наблюдать главн. мин. часть приращения. Для её выделения линеаризуем дифф. ур-е.
18) Линеаризация дифференциальных уравнений и ее использование при получении принципа максимума.
Линеаризация предназначена для того, чтобы заменить нелинейное диф. ур-ие окрест. некоторого решения и рассмотреть лин. ур-ие с малым отклонением от исходного решения (т.е. мы линеаризуем не объект, а решение диф. ур-ия, которое описывает данный объект в окрестн. известного решения).
Пример:
F(y, yl, u)=0, пусть y0(t)-реш. соотв. u0(t). Цель линеар. – получить новое решение
F(yн, yнl, uн(t))=0
Ищем yн(t). Для малых возмущений управляющего воздействия:
Uн(t)=U0(t)старое +E(t)возмущ.. Найти приближенный способ получения yн(t) – задача, которая стоит перед линеар-ей. Предполагается: yн(t) = y0(t) + x(t), где x(t)-малая добавка. Приближ. способ: для x(t) удается получить лин. диф. ур-ие, но оно будет с переменными коэф-ми.
Использование
линеаризации при получение принципа
максимума. F(y,
yl,
u)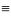 0;
u0(t)
– решение x0(t);
Uн(t)=U0(t)+Δt,
где Uн(t)
– новое управляющее воздействие.
xн(t)=x0(t)-δ(t)-новое
решение. Если Δt-очень
мало, считаем что δ(t)-тоже
мало. Если u0-известно,
то F(x0(t),
x0l(t),
u0(t))
0;
F(xн(t),
xнl(t),
uн(t))
0;
0;
u0(t)
– решение x0(t);
Uн(t)=U0(t)+Δt,
где Uн(t)
– новое управляющее воздействие.
xн(t)=x0(t)-δ(t)-новое
решение. Если Δt-очень
мало, считаем что δ(t)-тоже
мало. Если u0-известно,
то F(x0(t),
x0l(t),
u0(t))
0;
F(xн(t),
xнl(t),
uн(t))
0;
F(x0(t)+δ(t),
x0l(t)+δl(t),
u0(t))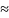 F(x0,
x0l,
u0)+
F(x0,
x0l,
u0)+ ,
где
,
где
 =a0(t),
=a0(t),
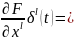 a1(t),
a1(t),
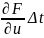 =b(t). Все производные – функции
времени. В окрест. решения x(t)
проводим разложение в ряд Фурье, т.к.
считаем, что
=b(t). Все производные – функции
времени. В окрест. решения x(t)
проводим разложение в ряд Фурье, т.к.
считаем, что
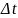 - мало, след-но. функция будет изменяться
мало, можно использ. первые два члена
разложения. a0(t),
a1(t),
b(t) – могут
быть вычислены, т.к. u0(t),
x0(t)-известны.
∑=0. Получаем:
a1(t)δ1(t)+
a0(t)δ(t)+b(t)
Δt
- мало, след-но. функция будет изменяться
мало, можно использ. первые два члена
разложения. a0(t),
a1(t),
b(t) – могут
быть вычислены, т.к. u0(t),
x0(t)-известны.
∑=0. Получаем:
a1(t)δ1(t)+
a0(t)δ(t)+b(t)
Δt
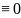 .
Задача: найти добавку δ(t),
для нее мы получим диф. ур-ие – это и
есть линеаризованное уравнение.
.
Задача: найти добавку δ(t),
для нее мы получим диф. ур-ие – это и
есть линеаризованное уравнение.
 δx(τ)
δx(τ)=
δx(τ)
δx(τ)=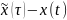 = ε(
= ε(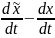 );
);
τ
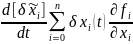 (x1….xn,u.)
–рез. линеаризации. δJ=δx0(t)=>0
хотим, чтобы функция имела наим знач→
приращ. в min д.б. “+”. Введем
числовой верх:
(x1….xn,u.)
–рез. линеаризации. δJ=δx0(t)=>0
хотим, чтобы функция имела наим знач→
приращ. в min д.б. “+”. Введем
числовой верх:
ψ=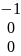 , -δx0(t)<=0,
-δJ =<δx(τ),ψ>;
ψ(t)=
, -δx0(t)<=0,
-δJ =<δx(τ),ψ>;
ψ(t)= ; ψ(t)=ψ; -δJ
=<δx(τ),ψ(t)>
; ψ(t)=ψ; -δJ
=<δx(τ),ψ(t)>
подберем
такой ψ(t), чтобы
<δx(τ),ψ(t)>=const,
потребуем чтобы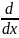 <δx(τ),ψ(t)>
;
необходимо чтобы выполнялось
<δx(τ),ψ(t)>
;
необходимо чтобы выполнялось
 – сопряж. диф. уравн. → обеспечим
<δx(τ),ψ(t)>=const.
Для того, чтобы u(t)
, было оптим-м. необх. чтобы в каждый
момент времени t функция
H=<f,ψ>
достигала наибольшего значения по
аргументу. u-главное
содержание принципа максимума.
– сопряж. диф. уравн. → обеспечим
<δx(τ),ψ(t)>=const.
Для того, чтобы u(t)
, было оптим-м. необх. чтобы в каждый
момент времени t функция
H=<f,ψ>
достигала наибольшего значения по
аргументу. u-главное
содержание принципа максимума.
