
Задания
1. Напишите
уравнения касательных, проведенных к
графику функции
![]() в точках пересечения графика с прямой
в точках пересечения графика с прямой
![]() .
.
2. При
каких значениях
касательная, проведенная к графику
функции
![]() в точке графика с абсциссой
в точке графика с абсциссой
![]() ,
проходит через точку
,
проходит через точку
![]() ?
?
3. При
каких значениях
прямая
![]() касается кривой
касается кривой
![]() ?
?
4. Найдите
все общие точки графика функции
![]() и касательной, проведенной к этому
графику через точку
и касательной, проведенной к этому
графику через точку
![]() .
.
5. Найдите
кратчайшее расстояние между параболой
![]() и прямой
и прямой
![]() .
.
6. На
кривой
![]() найдите точку, в которой касательная
к графику параллельна прямой
найдите точку, в которой касательная
к графику параллельна прямой
![]() .
.
7. Напишите
уравнение касательной к графику функции
![]() ,
которая касается его в двух точках.
Сделайте чертеж.
,
которая касается его в двух точках.
Сделайте чертеж.
8. Докажите,
что прямая
![]() не пересекает кривую
не пересекает кривую
![]() .
Найдите расстояние между их ближайшими
точками.
.
Найдите расстояние между их ближайшими
точками.
9. На
параболе
![]() взяты две точки с абсциссами
взяты две точки с абсциссами
![]() ,
,
![]() .
Через эти точки проведена секущая. В
какой точке параболы касательная к ней
будет параллельна проведенной секущей?
Напишите уравнения секущей и касательной.
.
Через эти точки проведена секущая. В
какой точке параболы касательная к ней
будет параллельна проведенной секущей?
Напишите уравнения секущей и касательной.
10. Найдите
угол
между касательными к графику функции
![]() ,
проведенными в точках с абсциссами
,
проведенными в точках с абсциссами
![]() и
и
![]() .
.
11. Напишите
уравнение всех общих касательных к
графикам функций
и
![]() .
.
12. При
каких значениях
прямая
![]() является касательной к графику функции
является касательной к графику функции
![]() ?
?
13. При
каких значениях
касательная, проведенная к графику
функции
![]() в точке с абсциссой
в точке с абсциссой
![]() ,
проходит через точку
,
проходит через точку
![]() ?
?
14. При
каком значении
![]() угол между кривыми
угол между кривыми
![]() и
и
![]() будет равен
?
будет равен
?
15.
При движении тела по прямой расстояние
(в метрах) от начальной точки изменяется
по закону
![]() .
Найти скорость (в м/с)
тела через 4
секунды после начала движения.
.
Найти скорость (в м/с)
тела через 4
секунды после начала движения.
16.
При движении тела по прямой скорость
(в м/с)
от начальной точки изменяется по закону
![]() .
Найти ускорение (в м/с2)
тела через 6
секунд после начала движения.
.
Найти ускорение (в м/с2)
тела через 6
секунд после начала движения.
Самостоятельная работа № 3. Исследование функций и построение графиков.
Цель работы: обобщить схему исследования функций и построение графиков функций по данным исследованиям.
Методические указания
Понятие производной − одной из важнейших в математике. С помощью производной, учитывая её механический и геометрический смысл, можно решать разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных стало возможным подробное исследование функции, что позволило очень точно строить их графики, находить промежутки возрастания и убывания, наибольшие и наименьшие значения и т.д.
Рассмотрим основные понятия, связанные с исследованием функции.
Возрастание и убывание функции. Точки экстремума.
Если
для любых двух значений аргумента
![]() и
и
![]() из условия
>
следует
из условия
>
следует
![]() >
>![]() ,
то функция
,
то функция
![]() называется возрастающей;
если для любых
и
из
условия
>
следует
<
,
то функция
называется возрастающей;
если для любых
и
из
условия
>
следует
<
,
то функция
![]() называется убывающей.
Функция, которая только возрастает
или только убывает, называется монотонной.
называется убывающей.
Функция, которая только возрастает
или только убывает, называется монотонной.
В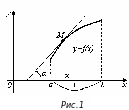 озрастание
и убывание функции
озрастание
и убывание функции
![]() характеризуется знаком ее производной:
если в некотором промежутке
характеризуется знаком ее производной:
если в некотором промежутке
![]() >0,
то функция возрастает в этом промежутке;
если же
<0,
то функция убывает в этом промежутке.
>0,
то функция возрастает в этом промежутке;
если же
<0,
то функция убывает в этом промежутке.
На
рисунке 1 изображен график возрастающей
и дифференцируемой на интервале
![]() функции
.
В каждой точке
функции
.
В каждой точке
![]() этого графика касательная составляет
с осью
этого графика касательная составляет
с осью
![]() острый угол
острый угол
![]() (
(![]() <
<
<
<![]() ).
Тангенсы острых углов положительны,
значит, согласно геометрического смысла
производной, и производная
).
Тангенсы острых углов положительны,
значит, согласно геометрического смысла
производной, и производная
![]() положительна для любых
положительна для любых
![]() из интервала
возрастания функции.
из интервала
возрастания функции.
Н а
рисунке 2 изображен график убывающей
на интервале
функции
.
Здесь для любой точки
графика функции угол
наклона касательной, проведенной к
графику функции, тупой (
<
<
а
рисунке 2 изображен график убывающей
на интервале
функции
.
Здесь для любой точки
графика функции угол
наклона касательной, проведенной к
графику функции, тупой (
<
<![]() ).
Тангенсы таких углов отрицательны, а
значит и производная
отрицательна.
).
Тангенсы таких углов отрицательны, а
значит и производная
отрицательна.
Т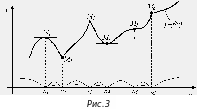 очки
экстремума функции – это те значения
ее аргумента
,
при которых функция
принимает экстремальные (пиковые)
значения – максимальные или минимальные.
Точек экстремума у функции
столько, сколько вершин и впадин у ее
графика.
очки
экстремума функции – это те значения
ее аргумента
,
при которых функция
принимает экстремальные (пиковые)
значения – максимальные или минимальные.
Точек экстремума у функции
столько, сколько вершин и впадин у ее
графика.
На
рисунке 3 изображен график непрерывной
функции
,
имеющей и интервалы возрастания, и
интервалы убывания, и точки экстремума.
Интервалы возрастания функции помечены
знаком
![]() ,
а интервалы убывания – знаком
,
а интервалы убывания – знаком
![]() .
.
Точками
экстремума данной функции являются
точки
![]() .
Причем точки
и
.
Причем точки
и
![]() – точки максимума, а
и
– точки максимума, а
и
![]() – точки минимума. Точки
– точки минимума. Точки
![]() и
и
![]() точками экстремума функции не являются,
так как соответствующие им точки графика
точками экстремума функции не являются,
так как соответствующие им точки графика
![]() и
и
![]() – не вершины и не впадины этого графика.
– не вершины и не впадины этого графика.
Точки экстремума разделяют интервалы возрастания и убывания функции. В точках максимума совершается переход от возрастания функции (слева от точки максимума) к ее убыванию (справа от точки максимума). То есть в точках максимума знак производной функции меняется с слева на справа. А в точках минимума, наоборот, совершается переход от убывания функции к ее возрастанию. То есть в точках минимума знак производной функции меняется с слева на справа.
Сами же точки экстремума не принадлежат ни к интервалам возрастания, ни к интервалам убывания функции. Потому в точках экстремума производная не может быть ни положительной, ни отрицательной. Значит, в этих точках она или равна нулю, или ее не существует вообще.
Этот
вывод понятен и с геометрической точки
зрения. Действительно, производная
функции связана с касательной к графику
функции (представляет собой тангенс
угла наклона этой касательной к оси
).
Но точкам экстремума функции
соответствуют на ее графике вершины и
впадины, в которых касательная к графику
или параллельна оси
(если вершина или впадина графика
округлая), или эта касательная отсутствует
вообще (если вершина или впадина острая).
В первом случае угол наклона
касательной к оси
равен нулю. Значит, и
![]() ,
а значит, и производная
,
а значит, и производная
![]() .
Во втором случае угол
не существует вообще, а значит, не
существует для данной точки экстремума
и производная
.
В частности, для рис рисунка 3 имеем:
.
Во втором случае угол
не существует вообще, а значит, не
существует для данной точки экстремума
и производная
.
В частности, для рис рисунка 3 имеем:
![]() ;
;
![]() – не существует;
– не существует;
![]() – не существует;
– не существует;
![]() .
.
Однако
заметим, что не любая точка
,
в которой производная равна нулю или
не существует, непременно будет точкой
экстремума. В частности, на рисунке
3
![]() ;
;
![]() не существует, и тем не менее ни точка
,
ни точка
не являются точками экстремума функции
.
не существует, и тем не менее ни точка
,
ни точка
не являются точками экстремума функции
.
Таким образом, лишь те точки (значения ), в которых производная функции равна нулю или не существует, могут быть точками экстремума этой функции. Но еще не факт, что все такие точки будут точками экстремума. Иначе говоря, точки (значения ), в которых или не существует, являются лишь подозрительными на экстремум. Чтобы выяснить суть каждой подозрительной точки, нужно посмотреть знак производной слева и справа от неё. Здесь возможны три варианта:
1) Если слева от подозрительной на экстремум точки знак производной , а справа , то эта подозрительная точка – точка максимума.
2) Если справа от подозрительной на экстремум точки знак производной , а справа , то эта подозрительная точка – точка минимума.
3) Если слева и справа от подозрительной на экстремум точки знак производной один и тот же, то эта подозрительная точка – не точка экстремума.
Для исследования функции на возрастание-убывание и точки экстремума применяют следующую схему:
1. Находим область определения функции. То есть находим все те значения , для которых существует (можно найти) значение функции . Заодно устанавливаем интервалы непрерывности и точки разрыва функции.
2. Находим производную .
3. Находим точки (значения ), подозрительные на экстремум. То есть находим те точки (значения ), в которых производная функции или равна нулю, или не существует.
4. Наносим все подозрительные на экстремум точки на область определения функции (на ось ) и фиксируем (например, дугами) интервалы, на которые разобьется область определения этими точками. Так как внутри каждого такого интервала производная функции существует и не обращается в нуль, то в каждом интервале производная сохраняет свой знак, который может измениться лишь при переходе к другому интервалу. С помощью вычисления производной в пробных внутренних точках определяем знак производной в каждом интервале. По найденным знакам производной устанавливаем интервалы возрастания и убывания функции, а по смене знака производной определяем точки экстремума функции (точки максимума и минимума).
В найденных точках максимума и минимума вычисляем значения функции и тем самым определяем вершины и впадины графика функции, отмечая заодно, округлые они или острые.
Пример
1.
Исследовать функцию
![]() на возрастание-убывание и точки
экстремума.
на возрастание-убывание и точки
экстремума.
Решение. Действуем по изложенной выше схеме.
1.
Функция
определена
(а следовательно, и непрерывна) для
любых,
то есть на всей числовой оси
(![]() <
<
<
<![]() ).
Значит, её график − сплошная (без
разрывов) линия.
).
Значит, её график − сплошная (без
разрывов) линия.
2.
Найдём производную
![]() :
:
![]()
3. Найдём точки (значения ), подозрительные на экстремум:
а)
![]()
б)
не существует
![]() таких
нет.
таких
нет.![]()
4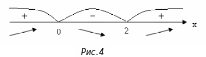 .
Нанесём найденные подозрительные на
экстремум точки
.
Нанесём найденные подозрительные на
экстремум точки
![]() и
и
![]() на область определения функции (на ось
).Ось
этими
точками разобьётся на три интервала:
на область определения функции (на ось
).Ось
этими
точками разобьётся на три интервала:
О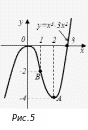 пределяем
знаки производной
пределяем
знаки производной
![]() в этих интервалах (они отмечены на
рисунке 4). Тем самым устанавливаем
интервалы возрастания функции
(они помечены стрелкой вверх) и интервалы
её убывания (стрелка вниз), а также
устанавливаем, что точка
− точка максимума функции, а точка
− точка её минимума.
в этих интервалах (они отмечены на
рисунке 4). Тем самым устанавливаем
интервалы возрастания функции
(они помечены стрелкой вверх) и интервалы
её убывания (стрелка вниз), а также
устанавливаем, что точка
− точка максимума функции, а точка
− точка её минимума.
5. Находим (вычисляем) значения функции в точках её максимума и минимума, устанавливая тем самым вершины и впадины графика функции:
![]() :
точка О
:
точка О![]() −вершина графика функции.
−вершина графика функции.
![]() :
точка А
:
точка А![]() −впадина графика функции.
−впадина графика функции.
6. В дополнение к проведённому исследованию найдём ещё точки пересечения графика с осями координат:
а)
С осью
:
![]()
![]()
![]() или
или
![]()
![]()
![]()
б)
С осью
![]() :
:
![]() .
.
По приведённому исследованию построим график (рисунок 5).
Выпуклость и вогнутость функции. Точки перегиба.
Н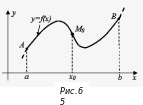 а
рисунке 6 изображен график функции,
выпуклой на интервале
а
рисунке 6 изображен график функции,
выпуклой на интервале
![]() ,
вогнутой на интервале
,
вогнутой на интервале
![]() ,
и у которой точка
,
и у которой точка
![]() ,
разделяющая интервалы выпуклости и
вогнутости, есть точка
перегиба функции.
,
разделяющая интервалы выпуклости и
вогнутости, есть точка
перегиба функции.
Точка
![]() называется точкой
перегиба графика функции
(не путать точку перегиба функции
и
точку перегиба её графика
).
называется точкой
перегиба графика функции
(не путать точку перегиба функции
и
точку перегиба её графика
).
Д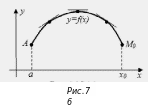 ля
выпуклой функции (рисунок 7) касательная
к ее графику в любой его точке расположена
выше графика, причем с увеличением
абсциссы
точки касания эта касательная
поворачивается по часовой стрелке. Это
значит, что с увеличением
угол наклона касательной к оси
уменьшается.
Но тогда уменьшается и угловой
коэффициент касательной
ля
выпуклой функции (рисунок 7) касательная
к ее графику в любой его точке расположена
выше графика, причем с увеличением
абсциссы
точки касания эта касательная
поворачивается по часовой стрелке. Это
значит, что с увеличением
угол наклона касательной к оси
уменьшается.
Но тогда уменьшается и угловой
коэффициент касательной
![]() .
А значит, с увеличением
уменьшается (убывает) равная ему
производная функции
.
Но если некая функция убывает, то, как
мы знаем, ее производная отрицательна.
Значит,
.
А значит, с увеличением
уменьшается (убывает) равная ему
производная функции
.
Но если некая функция убывает, то, как
мы знаем, ее производная отрицательна.
Значит,
![]() <0
на всем интервале
выпуклости функции
.
<0
на всем интервале
выпуклости функции
.
А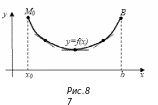 налогичное
рассуждение приводит к выводу, что
если функция
вогнута на некотором интервале
(смотри рисунок 8), то для любого
из этого интервала
налогичное
рассуждение приводит к выводу, что
если функция
вогнута на некотором интервале
(смотри рисунок 8), то для любого
из этого интервала
![]() >0
(проведите это рассуждение самостоятельно).
>0
(проведите это рассуждение самостоятельно).
Верно, естественно, и обратное: если на некотором интервале оси вторая производная функции положительна, то функция вогнута на этом интервале. А если эта производная отрицательна – то функция выпукла на указанном интервале.
Теперь перейдем к точкам перегиба функции. Так как эти точки разграничивают интервалы выпуклости и вогнутости и, следовательно, не принадлежат ни тем, ни другим, то в точках перегиба вторая производная функции не может быть ни положительной, ни отрицательной. А значит, в этих точках она или равна нулю, или не существует.
Но
не все точки
,
в которых
![]() или
не существует, непременно должны
быть точками перегиба. Точками перегиба
будут лишь те из них, в которых вторая
производная
меняет знак (с
на
или с
на
).
Таким образом, точки оси
,
в которых
или
не существует, являются лишь
подозрительными на перегиб. Окончательное
выяснение сути этих точек производится
после исследования знака второй
производной слева и справа от каждой
из них.
или
не существует, непременно должны
быть точками перегиба. Точками перегиба
будут лишь те из них, в которых вторая
производная
меняет знак (с
на
или с
на
).
Таким образом, точки оси
,
в которых
или
не существует, являются лишь
подозрительными на перегиб. Окончательное
выяснение сути этих точек производится
после исследования знака второй
производной слева и справа от каждой
из них.
Для исследования функции на выпуклость-вогнутость и точки перегиба применяют следующую схему:
1. Находим область определения функции, а заодно устанавливаем интервалы ее непрерывности и точки разрыва (стандартное начало любого исследования функции).
2. Находим вторую производную .
3. Находим точки (значения ), подозрительные на перегиб. То есть находим те точки (значения ), в которых вторая производная функции или равна нулю, или не существует.
3. Наносим все найденные подозрительные на перегиб точки на область определения функции (на ось ) и отмечаем (например, дугами) интервалы, на которые разобьется этими дугами область определения функции. В каждом из этих интервалов выясняем знак второй производной . По установленным знакам этой производной отмечаем интервалы выпуклости и вогнутости функции ( − вогнутость, − выпуклость), а также точки перегиба функции.
4. Вычисляем значения функции во всех найденных точках ее перегиба и находим тем самым точки перегиба графика функции.
Пример 2. Исследовать на выпуклость-вогнутость и точки перегиба функцию .
Решение. Используем изложенную выше схему.
1. Функция определена, а следовательно и непрерывна для любых от до .
2.
Найдём
![]() :
:![]() .
.
3. Найдём точки (значения ), подозрительные на перегиб:
а)
![]() .
.
б) не существует таких нет.
4.
Нанесём на ось
найденную подозрительную на перегиб
точку
![]() .
Ось
(область определения функции) разобьётся
этой точкой на два интервала:
.
Ось
(область определения функции) разобьётся
этой точкой на два интервала:
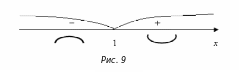
Определяем
знаки второй производной
![]() в этих интервалах (смотри рисунок 9). Тем
самым устанавливаем интервалы выпуклости
( знак
в этих интервалах (смотри рисунок 9). Тем
самым устанавливаем интервалы выпуклости
( знак
![]() )
и вогнутости (знак
)
и вогнутости (знак
![]() ),
а так же устанавливаем, что − точка
перегиба функции.
),
а так же устанавливаем, что − точка
перегиба функции.
5.
Вычисляем значение функции
в точке её перегиба.
![]() Тем самым определим точку
Тем самым определим точку
![]() перегиба графика функции. График функции
изображен на рисунке 5.
перегиба графика функции. График функции
изображен на рисунке 5.
Асимптоты.
Асимптоты графика функции – это такие линии (прямые или кривые), к которым неограниченно приближается указанный график при неограниченном его продолжении.
В
частности, на рисунке 10 изображен
график функции
,
имеющий три асимптоты: вертикальную
прямую
![]() ,
горизонтальную прямую
,
горизонтальную прямую
![]() и кривую
и кривую
![]() .
При этом, согласно этого рисунка,
вертикальная прямая
является асимптотой графика функции
лишь при
.
При этом, согласно этого рисунка,
вертикальная прямая
является асимптотой графика функции
лишь при
![]() (при
,
стремящемся к
(при
,
стремящемся к
![]() справа). При
справа). При
![]() (слева) эта прямая асимптотой графика
функции
не является. Горизонтальная прямая
является асимптотой графика функции
при
(слева) эта прямая асимптотой графика
функции
не является. Горизонтальная прямая
является асимптотой графика функции
при
![]() .
А кривая
является асимптотой графика этой
функции при
.
А кривая
является асимптотой графика этой
функции при
![]() .
.
Нахождение вертикальных асимптот.
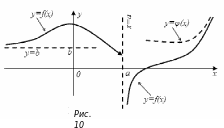 Рисунок
10 свидетельствует: если прямая
– вертикальная асимптота графика
функции
,
то должны выполняться два условия:
Рисунок
10 свидетельствует: если прямая
– вертикальная асимптота графика
функции
,
то должны выполняться два условия:
1) – точка разрыва функции ;
2)
![]() (
или
)
или
(
или
)
или
![]() (
или
)
(*)
(
или
)
(*)
И обратно, если выполняются оба условия (*), то прямая – вертикальная асимптота графика функции .
Таким образом для нахождения вертикальных асимптот графика функции :
1)
Находим все точки разрыва (![]() )
функции, то есть те изолированные точки
оси
,
в которых функция не определена.
)
функции, то есть те изолированные точки
оси
,
в которых функция не определена.
2) Каждую из точек разрыва проверяем на выполнимость второго условия (*).
Пример
3.
Найти вертикальные асимптоты графика
функции
![]() и сделать геометрическую иллюстрацию
полученного результата.
и сделать геометрическую иллюстрацию
полученного результата.
Решение.
Данная функция не определена, а
следовательно, разрывна лишь в двух
точках оси
:
![]() и
и
![]() .
Проверим каждую из них на выполнимость
второго условия (*):
.
Проверим каждую из них на выполнимость
второго условия (*):
![]()
![]()
![]()
![]()
Второе
условие (*) выполняется для точки
и не выполняется для точки
.
Значит, лишь прямая
является вертикальной асимптотой
графика нашей функции, причем и при
![]() ,
и при
,
и при
![]() .
А прямая
(ось
)
вертикальной асимптотой графика функции
не является. Геометрическая иллюстрация
полученных результатов дана на рисунке
11.
.
А прямая
(ось
)
вертикальной асимптотой графика функции
не является. Геометрическая иллюстрация
полученных результатов дана на рисунке
11.
Н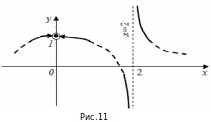 а
этом рисунке представлено лишь то, что
выяснено выше: поведение функции y
возле ее точек разрыва
и
.
Вдали от этих точек мы эту функцию
не исследовали, поэтому ее график не
известен (он лишь намечен пунктирной
линией).
а
этом рисунке представлено лишь то, что
выяснено выше: поведение функции y
возле ее точек разрыва
и
.
Вдали от этих точек мы эту функцию
не исследовали, поэтому ее график не
известен (он лишь намечен пунктирной
линией).
Нахождение невертикальных асимптот.
Рассматривая
рисунок 8, приходим к выводу: если
некоторая линия
![]() с уравнением
является невертикальной асимптотой
графика функции
при
или
,
то это значит, что при таком изменении
функция
с уравнением
является невертикальной асимптотой
графика функции
при
или
,
то это значит, что при таком изменении
функция
![]() ,
то есть
,
то есть
![]() ,
а значит
,
а значит
![]() ,
где
,
где
![]() при
или
(**).
при
или
(**).
И
обратно, при выполнении (**) функция
− асимптота функции
.
В частности, если
![]() ,
где
при
или при
(***), то соответственно при
или при
горизонтальная
прямая, будет асимптотой графика
функции
.
,
где
при
или при
(***), то соответственно при
или при
горизонтальная
прямая, будет асимптотой графика
функции
.
Чаще
всего асимптота графика функции − это
прямая, поэтому её уравнение в общем
виде можно записать
![]() .
Такую асимптоту называют наклонной.
Для отыскания коэффициентов
.
Такую асимптоту называют наклонной.
Для отыскания коэффициентов
![]() и
и
![]() применяют следующие формулы:
применяют следующие формулы:
![]() ,
,
![]() .
.
При
![]() имеет горизонтальную асимптоту
,
если же
или
раны
имеет горизонтальную асимптоту
,
если же
или
раны
![]() ,
то наклонных асимптот график функции
не имеет.
,
то наклонных асимптот график функции
не имеет.
Пример
4.
Найти невертикальные асимптоты графика
функции
![]() .
.
Решение.
Для нахождения нужно выяснить поведение
функции
![]() при
и при
.
при
и при
.
а)
Если
,
то очевидно, что
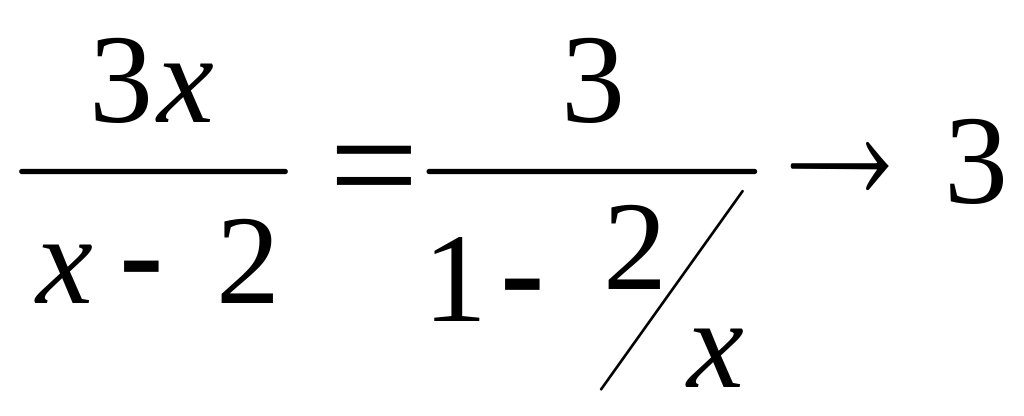 ;
;
![]() .
Поэтому при
функция
.
Поэтому при
функция
![]() .
А это значит, что прямая
с уравнением
.
А это значит, что прямая
с уравнением
![]() является асимптотой графика функции
при
.
является асимптотой графика функции
при
.
б)
Если
,
то очевидно, что
;
![]() .
Поэтому при
исходная функция
.
Поэтому при
исходная функция
![]() .
А это значит, что при
асимптотой графика функции
является горизонтальная прямая
.
А это значит, что при
асимптотой графика функции
является горизонтальная прямая
![]() .
.
Пример
5.
Найти наклонную асимптоту графика
![]() .
.
Решение. Найдем коэффициенты наклонной асимптоты
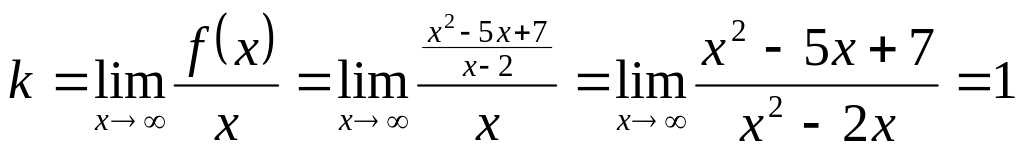 ,
,
![]() .
.
Таким
образом наклонная асимптота имеет вид
![]() .
.
Пример
6.
Определить все имеющиеся асимптоты
графика функции
![]()
и изобразить поведение этого графика возле его асимптот.
Решение. Начнем с нахождения области определения функции y. Функция определена, а следовательно, и непрерывна для всех x, кроме x=1. То есть x=1 – единственная точка разрыва нашей функции. А значит, вертикальная прямая x=1, проходящая через эту точку – единственная возможная вертикальная асимптота графика нашей функции.
Проверим, действительно ли она – вертикальная асимптота. Для этого выясним, в соответствии с (*), поведение функции y при x→1+0 и при x→1-0:
![]() ;
;
![]() .
.
То
есть
![]() при
при
![]() и
и
![]() при
при
![]() .
А это значит, что вертикальная прямая
является вертикальной асимптотой
графика функции
,
причём и при
,
и при
.
.
А это значит, что вертикальная прямая
является вертикальной асимптотой
графика функции
,
причём и при
,
и при
.
Т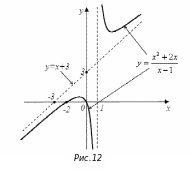 еперь
поищем возможные не вертикальные
асимптоты. Для этого найдем коэффициенты
и
.
еперь
поищем возможные не вертикальные
асимптоты. Для этого найдем коэффициенты
и
.
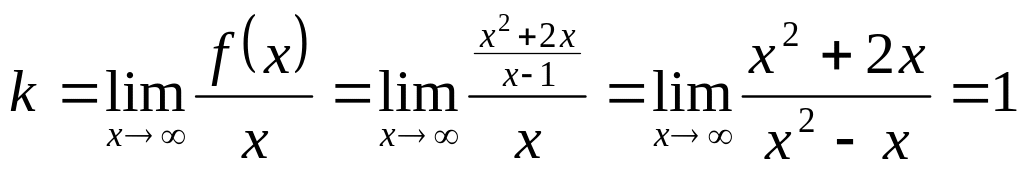 ,
,
![]()
![]() .
.
Значит
наклонная асимптота имеет вид
![]() .
.
Теперь построим график функции (смотри рисунок 12).
Общая схема исследования функции
Пусть – некоторая заданная функция. Требуется провести ее всестороннее (полное) исследование и построить ее график. Указанное полное исследование функции можно провести по следующей схеме.
1. Находим область определения функции. Заодно устанавливаем интервалы ее непрерывности и точки разрыва.
2.
Исследуем функцию на четность-нечетность
и тем самым устанавливаем возможную
симметрию графика функции (относительно
оси
или относительно начала координат). Для
этого записываем выражение
![]() и сравниваем его с
:
и сравниваем его с
:
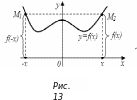
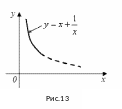
а)
Если
![]() ,
функция
− четная. Её график симметричен
относительно оси
(рисунок 13).
,
функция
− четная. Её график симметричен
относительно оси
(рисунок 13).
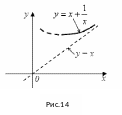
б)
Если
![]() ,
то функция
− нечетная. Её график симметричен
относительно начала координат (рисунок
14).
,
то функция
− нечетная. Её график симметричен
относительно начала координат (рисунок
14).
в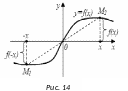 )
Если не имеет место ни вариант (а) ни
вариант (б), то функция
− общего вида (её график симметрией
(а) и (б) не обладает).
)
Если не имеет место ни вариант (а) ни
вариант (б), то функция
− общего вида (её график симметрией
(а) и (б) не обладает).
3. Исследуем функцию на периодичность (на повторяемость ее графика). Из элементарных функций это имеет смысл делать лишь для тригонометрических функций, ибо прочие функции заведомо не периодичны.
4. Исследуем поведение функции возле найденных в пункте 1 точек ее разрыва, а также возле границ области ее определения, учитывая при этом информацию, полученную в пунктах 2 и 3. Заодно устанавливаем (определяем) вертикальные и невертикальные асимптоты графика функции
5. Находим интервалы возрастания и убывания функции и точки ее экстремума (с помощью первой производной y′=f′(x)). Заодно находим вершины и впадины графика функции и устанавливаем их тип (округлые; острые).
6. Находим интервалы выпуклости и интервалы вогнутости функции и точки ее перегиба (с помощью второй производной y′′=f′′(x)). Заодно находим точки перегиба графика функции.
7. Находим точки пересечения графика функции с осями координат.
8. Строим график функции.
Пример
7.
Провести полное исследование функции
![]() и построить её график.
и построить её график.
Решение. Реализуем изложенную выше схему.
1. Область определения функции − любые , кроме . То есть функция определена (а следовательно, и непрерывна) на всей числовой оси , кроме точки , которая, таким образом, является единственной точкой разрыва функции.
2.
Исследуем функцию
на чётность-нечётность. Имеем:
![]() ;
тогда
;
тогда
![]() .
Как видим,
.
Значит, наша функция − нечётная, её
график симметричен относительно начала
координат. А значит, дальнейшем достаточно
исследовать функцию лишь для
>
.
Как видим,
.
Значит, наша функция − нечётная, её
график симметричен относительно начала
координат. А значит, дальнейшем достаточно
исследовать функцию лишь для
>![]() ,
так как для
<
можно будет учесть указанную выше
симметрию.
,
так как для
<
можно будет учесть указанную выше
симметрию.
3. Функция − алгебраическая (не тригонометрическая), а следовательно, не периодическая.
4.
Исследуем функцию возле точки её разрыва
(справа, при
![]() ),
а так же при
(на правой границе области её определения):
),
а так же при
(на правой границе области её определения):
а)
При
функция
![]() .
То есть
.
То есть
![]() (
при
).
(
при
).
А это значит, что вертикальная прямая с уравнением (осью ) является вертикальной асимптотой графика функции. К ней справа (при ) неограниченно приближается к графику функции, устремляясь при этом вверх (рисунок 13):
б) Найдем наклонную асимптоту графика функции. Для этого найдем коэффициенты коэффициенты и .
 ,
,
![]() .
.
Значит
наклонная асимптота имеет вид
![]() .
Причём график функции
при
стремиться к прямой
.
Причём график функции
при
стремиться к прямой
![]() сверху, так как
сверху, так как
![]() >
для всех
>
0 (рисунок 14).
>
для всех
>
0 (рисунок 14).
5. Найдем интервалы возрастания и убывания и точки экстремума функции (схема исследования изложена выше).
а)
Находим производную
:
![]()
Точку x=0 исследовать не будем, так как она не входит в область определения функции. Не будем исследовать и отрицательную точку x2=-1 (см. пункт 2).
в) Нанесем оставшуюся подозрительную на экстремум точку x1=1 на область определения функции (на ось ох). При этом ограничимся рассмотрением лишь положительной полуоси x>0:

В
обоих получившихся интервалах найдем
знак производной y′
и отметим его. Тем самым устанавливаем
интервал возрастания
![]() и интервал убывания
и интервал убывания
![]() функции. Заодно устанавливаем, что
– точка минимума функции.
функции. Заодно устанавливаем, что
– точка минимума функции.
г) Найдем значение функции в точке минимума и тем самым определим впадину графика функции:


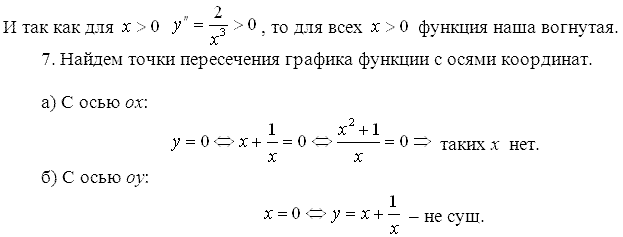
Таким образом, ни с осью , ни с осью график нашей функции не пересекается.
8. Строим график функции – сначала для x>0, а затем, по симметрии относительно начала координат, и для x<0 (рисунок 15).
ЗАДАНИЯ
Провести полное исследование и построить графики функций
1.
а)![]() ,
б)
,
б)
![]()
2.
а)
![]() ,
б)
,
б)
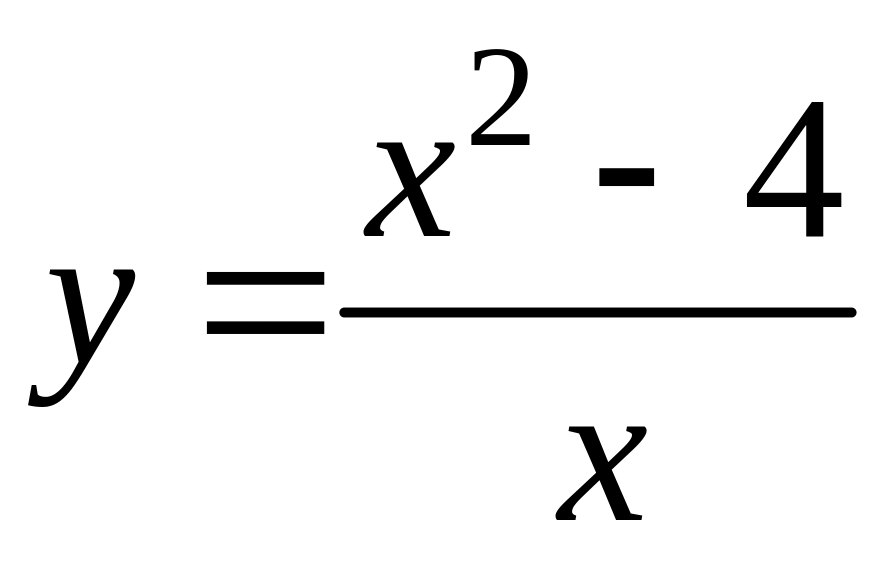
3.
а)
![]() ,
б)
,
б)
![]()
4.
а)
![]() ,
б)
,
б)
![]()
5.
а)
![]() ,
б)
,
б)
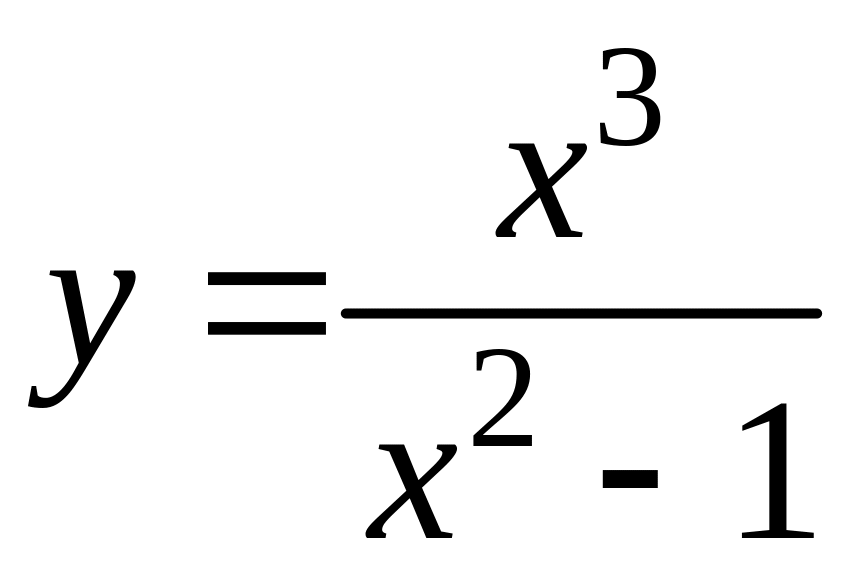
6.
а)![]() ,
б)
,
б)
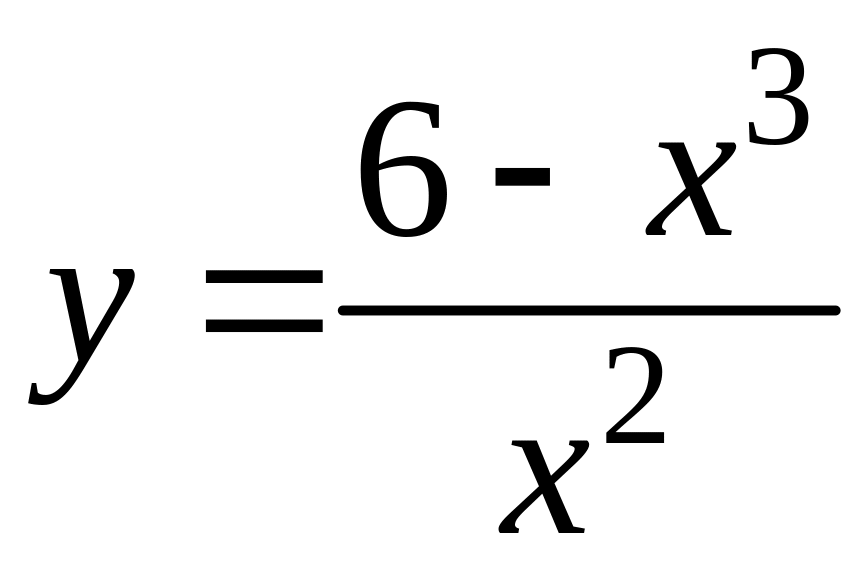
САМОСТОЯТЕЛЬНАЯ РАБОТА № 4.
Дифференциал. Применение дифференциала в приближенных вычисления.
Цель работы: познакомится с понятием дифференциала, научится вычислять дифференциал функции и применять дифференциал в приближенных вычислениях.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Понятие дифференциала функции
Пусть функция имеет в точке отличную от нуля производную
![]() .
.
Тогда,
по теореме о связи функции, ее предела
и бесконечно малой функции, можно
записать
![]() ,
где
,
где
![]() при
при
![]() ,
или
,
или
![]() .
.
Таким
образом, приращение функции
![]() представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых
![]() и
и
![]() ,
являющихся бесконечно малыми при
.
При этом первое слагаемое есть бесконечно
малая функция одного порядка с
,
являющихся бесконечно малыми при
.
При этом первое слагаемое есть бесконечно
малая функция одного порядка с
![]() ,
так как
,
так как
![]() ,
а второе слагаемое есть бесконечно
малая функция более высокого порядка,
чем
то
,
а второе слагаемое есть бесконечно
малая функция более высокого порядка,
чем
то
![]()
![]() .
.
Поэтому первое слагаемое называют главной частью приращения функции .
Дифференциалом
функции
в точке
называется главная часть ее приращения,
равная произведению производной функции
на приращение аргумента, и обозначается
![]() (или
(или
![]() ):
):
![]() .
(1)
.
(1)
Дифференциал называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной , т. е. дифференциал функции .
Так
как
![]() ,
то, согласно формуле (1), имеем
,
то, согласно формуле (1), имеем
![]() ,
т. е. дифференциал независимой переменной
равен приращению этой переменной:
,
т. е. дифференциал независимой переменной
равен приращению этой переменной:
![]() .
.
Поэтому формулу (1) можно записать так
![]() ,
(2)
,
(2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из
формулы (2) следует равенство
![]() .
Теперь обозначение производной
.
Теперь обозначение производной
![]() можно рассматривать как отношение
дифференциалов
и
можно рассматривать как отношение
дифференциалов
и
![]() .
.
Пример
1.
Найти дифференциал функции
![]() .
.
Решение:
По формуле
находим
![]() .
.
Пример
2.
Найти дифференциал функции
![]() .
Вычислить
при
.
Вычислить
при
![]() .
.
Решение:
![]() .
.
Подставив
![]() и
и
![]() ,
получим
,
получим
![]() .
.
Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
Для
этого проведем к графику функции
в точке
![]() касательную
касательную
![]() и рассмотрим ординату этой касательной
для точки
и рассмотрим ординату этой касательной
для точки
![]() (см.
рис.). На рисунке
(см.
рис.). На рисунке
![]() .
Из прямоугольного треугольника
.
Из прямоугольного треугольника
![]() имеем:
имеем:
![]() ,
т.е.
,
т.е.
![]() .
.
Но,
согласно геометрическому смыслу
производной,
![]() .
Поэтому
.
Поэтому
![]() .
.
Сравнивая
полученный результат с формулой (1),
получаем
![]() ,
т.
е. дифференциал
функции
в точке
равен приращению ординаты касательной
к графику функции в этой точке, когда
получит приращение
.
,
т.
е. дифференциал
функции
в точке
равен приращению ординаты касательной
к графику функции в этой точке, когда
получит приращение
.
В этом и состоит геометрический смысл
дифференциала.
этом и состоит геометрический смысл
дифференциала.
Основные теоремы о дифференциалах
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции ( ) и соответствующие теоремы о производных.
Например,
так как производная функции
![]() равна нулю, то дифференциал постоянной
величины равен нулю:
равна нулю, то дифференциал постоянной
величины равен нулю:
![]() .
.
Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:
Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.
Таблица дифференциалов
![]()
![]() ,
в частности
,
в частности
![]()
![]() ,
в частности
,
в частности
![]()
![]() ,
если
,
если
![]() ,
если
,
если
![]()
![]()
![]()
![]() ,
в частности
,
в частности
![]()
![]() ,
в частности
,
в частности
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Применение дифференциала к приближенным вычислениям
Как
уже известно, приращение
функции
в точке
можно представить в виде
,
где
при
,
или
![]() .
Отбрасывая бесконечно малую
более высокого порядка, чем
,
получаем приближенное равенство
.
Отбрасывая бесконечно малую
более высокого порядка, чем
,
получаем приближенное равенство
![]() ,
(3)
,
(3)
причем это равенство тем точнее, чем меньше .
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.
Пример
3.
Найти приближенное значение приращения
функции
![]() при
при
![]() .
.
Решение:
Применяем формулу (3) получаем
![]() .
.
![]()
Итак,
![]() .
.
Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем :
![]()
![]() .
.
![]()
Абсолютная
погрешность приближения равна
![]() .
.
Подставляя
в равенство (3) значения
и
,
получим
![]() или
или
![]() (4)
(4)
Формула (4) используется для вычислений приближенных значений функций.
Пример
4.
Вычислить приближенно
![]() .
.
Решение:
Рассмотрим функцию
![]() .
По формуле (4) имеем
.
По формуле (4) имеем
![]() ,
т. е.
,
т. е.
![]() .
.
Так
как
![]() ,
то при
,
то при
![]() получаем
получаем
![]() .
.
Пример
5.
Вычислить приближенно
![]() ,
при
,
при
![]() .
.
Решение:
Рассмотрим функцию
![]() .
По формуле (4) имеем
.
По формуле (4) имеем
![]() ,
т. е.
,
т. е.
![]() .
.
Так
как
![]() ,
то при
,
то при
![]() (
(![]() )
получаем
)
получаем
![]() .
.
Пример
6.
Какой путь пройдет тело при свободном
падении на Луне за
![]() от начала падения. Уравнение свободного
падения тела
от начала падения. Уравнение свободного
падения тела
![]() ,
,
![]() .
.
Решение:
Требуется найти ![]() .
Воспользуемся приближенной формулой
.
Воспользуемся приближенной формулой
![]() ,
т.е.
,
т.е.
![]() .
При
.
При
![]() и
и
![]() ,
,
![]() ,
находим
,
находим
![]() .
.
ЗАДАНИЯ
![]()
Задача (для самостоятельного решения). Тело массой m=20 кг движется со скоростью ν=10,02 м/с. Вычислить приближенно кинетическую энергию тела
![]()
САМОСТОЯТЕЛЬНАЯ РАБОТА № 5.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Цель работы: познакомится с линейными однородными дифференциальными уравнениями второго порядка, научится находить общее решение таких уравнений.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Определение.
Линейным однородным дифференциальным
уравнением второго порядка с постоянными
коэффициентами
называется
уравнение вида
![]() ,
где
и
,
где
и
![]() – постоянные величины.
– постоянные величины.
Для практического использования алгоритм решения таких уравнений удобно оформить в виде таблицы:
Дифференциальное уравнение |
|
||
Характеристическое уравнение |
|
||
Дискриминант
|
|
|
|
Корни характеристического уравнения |
|
|
|
Множества решений |
|
|
|
Пример
1.
Решить
уравнение
![]() .
.
Решение.
Составим
характеристическое уравнение
![]() .
.
![]() .
.
Следовательно,
характеристическое уравнение имеет
два различных действительных корня.
Определим их:
![]() .
.
Общее
решение
данного
уравнения имеет вид
![]() .
.
