Тема 4.2. Алгебраїчні моделі формальних мов

Вказівки щодо використання літературних джерел.

Вправи до теми 4.2.

Розділ 5. ТЕОРІЯ АВТОМАТІВ

У розділі вказана рекомендована література з кожної теми розділу, описані труднощі, які можуть виникнути при самостійному вивченні матеріалу, та способи подолання їх, наводяться вправи та приклади їх виконання.

Тема 5.1. Скінчені автомати, їх аналіз і синтез

[1, гл.2, розд.2, § 3. 4, розд.3, §1, 2; гл.3, § 1- 6; 4, гл.16, § 6А; 11, гл.1, § 1- 10; гл.2, § 1- 3, 5, 6, 8-12, гл.3, §16, гл.4, §1- 8, гл.5, § 1- 3, гл.6, § 4, 5; 13, гл.7; 22, передмова, гл.1, вступ]

Вказівки щодо використання літературних джерел.

Починаючи з уявлення про скінчений автомат і скінчений розпізнавач, необхідно розглянути різні способи їх задання і влас­тивості [2; 11], дослідити зв’язок регулярних виразів, скінчен­их автоматів і автоматних граматик як різних способів задання регулярних мов [1; 4; 16].

Тут дуже важливо і зручно порівняти мови L₁ і L₂ як такі, що L₂  L₁ : L₁ = {, 0, 1, 00, 01, 10, 11, ...}, L₂ = {, 01, 0011, 000111,...}. Для мови L₁ досить нескладно запропонувати регулярний вираз (0+1)* i граф переходів розпізнавача.

Легко побудувати й граматику Хомського, яка породжує мову L₁ : G = <{d₀}, {0, 1}, {d₀  0d₀ , d₀  1d₀}, d₀>.

Таким чином, L₁ - регулярна мова.

Здавалося б, мову L₂ також можна без особливих ускладнень задати регулярним виразом, скінченим розпізнавачем або автоматною граматикою Хомcького, адже L₁  L₂.

Проте зробити це неможливо.

0

Дійсно, скінчений розпізнавач повинен для цього мати здатність виконувати підрахунок кількості символів “0” і “1” при нескінченій кількості слів мови, що вочевидь неможливо.

У граматиках це можна було б зробити, використовуючи один із двох підходів:

1. включити в множину правил виведення граматики правила, що забезпечують симетричне породження символів “0” і “1” за рахунок відповідного добору нетерміналів, наприклад d₀  0d₀1, d₀   або d₀  0d₁, d₁  d₀1, d₀   (але тоді це буде вже не будуть автоматні граматики, тому що у першому випадку отримали правила виведення контекстно-вільної граматики, а у другому - ліволінійної граматики);

2. підібрати множину правил виведення і ввести порядок їх виконання у процесі породження слів так, щоб поява символу “0” неодмінно супроводжувалася появою символу “1” (тобто використати аналог типової для програмування впорядкованості операторів), наприклад:

(1) d₀  0d₀

(2) d₀ 1d₀

(3) d₀ 

Якщо правила виведення використовувати тільки в порядку (1) - (2) - ... - (1) - (2) - (3), то отримаємо мову L₂, але граматики Хомського такої здатності не мають і, таким чином, як продемонстровано вище така множина правил автоматної граматики породжує мову L₁.

Отже, кожна регулярна мова - контекстно-вільна, але існують контекстно-вільні мови, наприклад мова L₂, які не є регулярними, а також може виявитися, що знайдеться регулярна мова L₁ така, що L₁  L₂.

Тут, природно, виникають такі запитання:

І) чи завжди для контекстно-вільної мови L₂ знайдеться регулярна мова L₁ така, що L₁  L₂?

2) чи можна використовувати порядок виконання правил виведення для розширення можливостей граматики породження?

Спробуйте відповісти на ці запитання, навіть якщо це здасться дуже складним. У будь-якому разі відповіді на поставлені запитання знайдете далі.

Варто спробувати змоделювати відомий реальний об’єкт у вигляді скінченого автомата.

Реальне застосування скінчених автоматів неможливе без розв’язання задач аналізу або синтезу скінчених автоматів. Тому рекомендується глибоко дослідити постановку й методи розв’язання цих задач [2; 11; 16; 28] і розглядати тільки алгоритми абстрактного синтезу автоматів.

Варто сформувати уявлення про еквівалентні стани й автомати, мінімальну форму автомата та її важливість для реальних об'єктів, що описуються скінченими автоматами, вивчити алгоритми мінімізації та еквівалентного розбиття, порівняти стрічкові автомати й нейронні мережі як два види задання скінчених автоматів [13].

Необхідно сформувати уявлення про проблему розпізнавання у загальному плані [22], а потім проаналізувати проблему розпізнавання слів мови та експерименти з розпізнавання станів скінченого автомата [11] як важливі її застосування.

Гідно пильної уваги те, що автомати дозволяють моделювати поведінку різноманітних об’єктів у часі. Ця поведінка визначається у вигляді обумовленої реакції об’єкта на ті чи інші події. Такий підхід до визначення поведінки можна застосовувати для моделювання функціонування об’єктів у реальному часі. Умови можуть

Варто зазначити певне нерозуміння студентами “механічності” функціонування автомата. Тому треба формувати уявлення про об’єкт, поведінка якого обумовлена у всіх випадках його застосування, позбавлений всілякого інтелекту. Автомат може здійснювати ті дії і переходи, які визначені його функціями виходів і переходів. Інтелект належить творцям автоматів, які механічно відтворюють закладену в них поведінку.

Вправи до теми 5.1.

Вправа І. Скінченний автомат заданий таблицею переходів

	a i+1			bi
	e1	e2	e3	e1	e2	e3
a1	a5	a2	a1	b1	b1	b2
a2	a2	a3	-	b2	b2	b3
a3	-	-	-	-	-	-
a4	a3	a7	-	b1	b2	-
a5	-	-	-	-	-	-
a6	-	-	-	-	-	-
a7	-	-	a7	-	-	b2

Необхідно:

І) задати автомат графом переходів;

2) задати автомат матрицею переходів;

З) визначити вихідну послідовність при подачі на вхід такої програми:

а) e₂ e₁ e₁ e₃; б) e₃ e₃ e₂ e₂; в) e₃ e₁ ;

г) e₃ e₂ e₁ e₂ e₂; д) e₂ e₃ e₂ e₃,

якщо автомат знаходиться у стані a₁;

4) визначити досяжну множину для стану a₁ ;

5) визначити тупикові, перехідні та ізольовані стани;

6) визначити множину G_L(А_L), де a) А_L = {a₁, a₂}; б/ А_L = {a₁, a₄}; в) А_L = {a₂ , a₄};

7) визначити множину H_L(А_L), де a) А_L = {a₁, a₂}; б) А_L = {a₁, a₄};

8) знайти множину всіх маршрутів довільної довжини між парами станів: а) (a₁, a₅); б) (a₁, a₃);

9) знайти шляхи, коротші від усіх інших, що з’єднують кожну пару станів.

Вправа 2. Скінчений автомат Мура, заданий у вправі 1, задати як скінчений автомат Мілі, що визначає таке ж відображення.

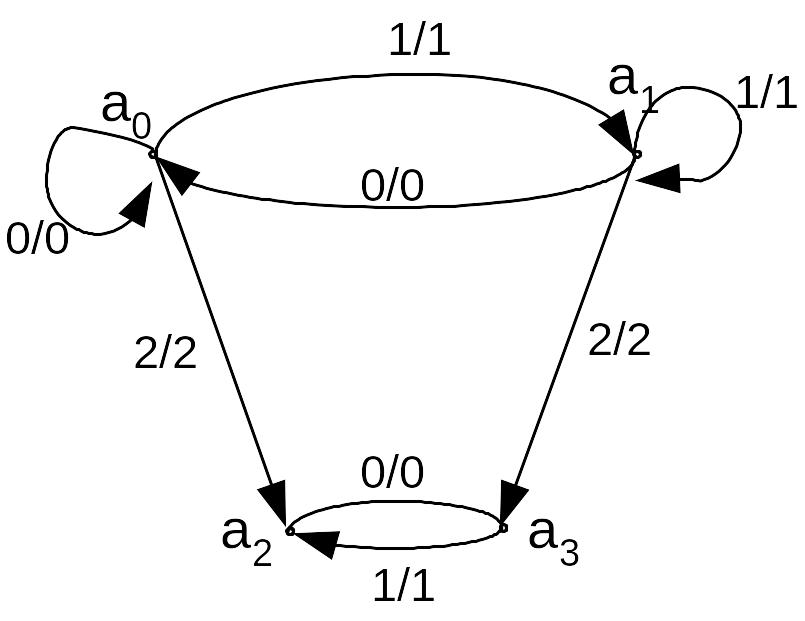
Вправа 3. Задати за допомогою граматики або інших засобів мову, яку допускає такий скінчений автомат:

І)

якщо a₀ - початковий стан; a₂ - заключний стан.

Як зміниться мова, що допускається автоматом, якщо:

а) початковим станом автомата визначити стан a₁;

б) граф переходів автомата об’єднати з графом, який містить одне ребро ( a₂, a₂);

2 ) 3)

a₀ - початковий стан; a ₄ - заключний стан;

4 ) 5)

a₀ - початковий стан; a₀ - початковий стан;

a₂ - заключний стан; a₂ - заключний стан;

6 ) 7)

a₀ - початковий стан; a₀ - початковий стан;

a₁ - заключний стан; a₂ - заключний стан.

Приклад: Граф переходів скінченного автомата має такий вигляд:

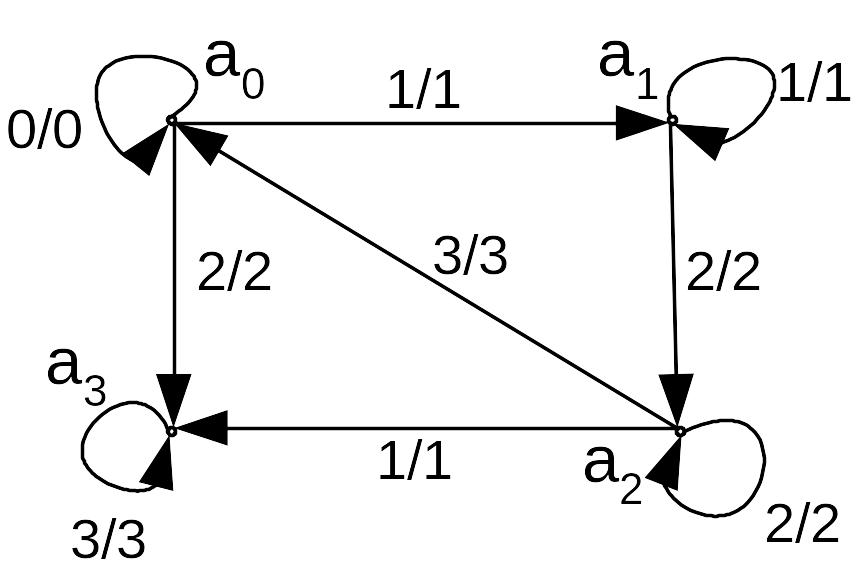
початковий стан - a₀ ; заключний стан - a₃. Автомат допускає слово е_i1,…, е_im, якщо існує орієнтований маршрут із a₀ в а₃, ребро якого e_l (1 l m ) помічене вхідним символом е_il. Цей скінчений автомат допускає слова, що мають вигляд

a ) 0…0 1…1 2…2 3 0…0 2 3…3,

де n₁, n₅, n₆  0; n₂, n₃, n₄  1;

б) 0…0 1…1 2…2 1 3… 3, де n₁, n₆  0; n₂, n₃  1;

в/ 0…0 2 3…3, де n₁, n₃  0.

n₁

n₃

Так, слова, що мають вигляд а), допустимі, бо автомат можна перевести із стану а₀ в стан а₃ орієнтованим маршрутом (а₀ , а₀ ), (а₀ , а₁ ), (а₁ , а₁ ), (а₁ , а₂ ), (а₂ , а₂ ), (а₂ , а₀ ), (а₀ , а₀ ), (а₀ , а₃ ), (а₃ , а₃ ), причому петлі (а₀ , а₀ ), (а₁ , а₁ ), (а₂ , а₂ ), (а₃ , а₃ ) можна повторити довільне число разів, також як довільне число разів можна повторити цикл (а₀ , а₀ ), (а₀ , а₁ ), (а₁ , а₁ ), (а₁ , а₂ ), (а₂ , а₂ ), (а₂ , а₀ ), який є складовою частиною маршруту.

Необхідно зазначити, що діапазони повторів різних символів слів, що мають вигляд а), різні, наприклад, п₁ і п₂ . Це пов’язано із тим, що п₁ - кількість повторів петлі, яких може не бути, а п₂ містить ще ребро (а₀ , а₁ ).

Вправа 4. Навести скінчений автомат для описання функціонування якого-небудь реального об’єкту.

Приклад: Прилад приймає у довільному наборі дрібні монети та видає картку вартістю 2 коп. Користувач має можливість вибрати одну з кількох видів карток. Якщо сума не набрана, то користувач попереджується приладом і може вимагати повернення грошей. Коли потрібна сума набрана, то автомат інформує користувача про це. Усі монети, відмінні від одно- та двокопійчаних монет, та інші речі повертаються без попередження.

Функціонування приладу описує автомат М = < E, A, В, f₁, f₂, >, де

E = {1, 2, e₁, e₂, e₃, В, M} - множина вхідних символів;

A = {a₀, a₁, a₂ , a₃} - множина станів;

B = {b₁, b₂ , b₃ , b₄, b₅ , b₆, b₇ , b₈, b₉ , b₁₀} - множина вихідних символів;

f₁, f₂ - функції відповідно переходу та виходу, задані таблицею.

a i+1

b i

1

2

e1

e2

e3

B

M

1

2

e1

e2

e3

B

M

a0

a1

a2

a0

a

a0

a0

a0

b1

b2

b3

b3

b3

b3

b4

a1

a2

a3

a1

a1

a1

a0

a1

b1

b2

b3

b3

b3

b5

b4

a2

a2

a2

a0

a0

a0

a0

a2

b5

b6

b7

b8

b9

b6

b4

a3

a3

a3

a1

a1

a1

a0

a3

b5

b6

b7

b8

b9

b10

b4

Символи множин E i В :

1 - користувач кидає монету вартістю 1 коп.;

2 - користувач кидав монету вартістю 2 коп.;

е₁ - користувач вимагає картку типу 1;

е₂ - користувач вимагає картку типу 2;

е₃ - користувач вимагає картку типу 3;

B - користувач вимагає повернення грошей;

M - користувач кидає довільну річ або монету, відмінну від

монети вартістю в 1або 2 коп.;

b₁ - користувача повідомляють, що кинута монета вартістю 1 коп.;

b₂ - користувача повідомляють, що сума набрана;

b₃ - прилад сигналізує, що від нього вимагають те, на що не мають права;

b₄ - користувачу повертають погану монету чи річ;

b₅ - користувачу повертають монету вартістю 1 коп.;

b₆ - користувачу повертають монету або набір на суму 2 коп;

b₇ - користувачу видається картка типу 1;

b₈ - користувачу видається картка типу 2;

b₉ - користувачу видається картка типу 3;

b₁₀ - користувачу повертають набір монет на суму 3 коп.

Вправа 5. Для автоматів, заданих у вправі 3, побудувати скінчені автомати, які покривають їх.

Вправа 6. Скінчений автомат задано такою таблицею переходів:

	ai+1		bi
	e1	e2	e1	e2
a1	a3	a8	b1	b2
a2	a3	a8	b1	b2
a3	a1	a2	b2	b3
a4	a6	a4	b1	b2
a5	a1	a2	b2	b3
a6	a4	a6	b1	b2
a7	a3	a5	b1	b2
a8	a7	a2	b1	b3

Необхідно:

І) знайти всі двоеквівалентні стани;

2) знайти всі триеквівалентні стани;

З) знайти всі еквівалентні стани;

4) знайти пару дворозрізнюваних станів;

5) знайти пару трирозрізнюваних станів;

6) побудувати еквівалентне розбиття;

7) знайти мінімальну форму.

Вправа 7. Знайти мінімальні форми скінчених автоматів, заданих такими таблицями переходів:

1)	ai+1		bi
	0	1	0	1
a1	a1	a2	b1	b2
a2	a2	a1	b1	b2
a3	a5	a6	b2	b3
a4	a5	a6	b2	b3
a5	a1	a2	b1	b3
a6	a1	a2	b1	b3
a7	a9	a10	b1	b2
a8	a8	a7	b1	b2
a9	a3	a4	b1	b3
a10	a3	a4	b1	b3

2)	ai+1		bi
	0	1	0	1
a1	a3	a3	b1	b2
a2	a3	a3	b1	b2
a3	a5	a6	b3	b1
a4	a6	a7	b2	b1
a5	a6	a6	b2	b1
a6	a1	a2	b2	b3
a7	a1	a2	b2	b3
a8	a8	a9	b1	b2
a9	a9	a1	b1	b3

3)	ai+1		bi
	0	1	0	1
a1	a2	a3	b1	b2
a2	a3	a4	b2	b3
a3	a4	a6	b1	b3
a4	a3	a4	b1	b3
a5	a9	a10	b2	b3
a6	a10	a9	b2	b3
a7	a8	a9	b1	b3
a8	a9	a10	b1	b3
a9	a1	a2	b1	b2
a10	a1	a2	b1	b2

4)	ai+1			bi
	e1	e2	e3	e1	e2	e3
a1	a2	a5	a6	b1	b2	b2
a2	a3	a4	a3	b2	b2	b3
a3	a3	a4	a2	b2	b2	b3
a4	a8	a9	a2	b2	b1	b3
a5	a9	a8	a5	b2	b1	b3
a6	a6	a7	a1	b1	b2	b3
a7	a7	a6	a2	b1	b2	b3
a8	a2	a3	a7	b2	b2	b3
a9	a2	a3	a7	b2	b2	b3

5)	ai+1			bi
	e1	e2	e3	e1	e2	e3
a1	a1	a1	a2	b1	b1	b3
a2	a1	a1	a1	b1	b1	b3
a3	a5	a7	a8	b2	b2	b3
a4	a5	a7	a8	b2	b2	b3
a5	a1	a1	a3	b2	b3	b1
a6	a2	a3	a1	b2	b3	b1
a7	a8	a7	a1	b1	b2	b3
a8	a7	a8	a2	b1	b2	b3
a9	a9	a10	a11	b2	b2	b3
a10	a10	a9	a11	b2	b2	b3
a11	a5	a6	a10	b1	b2	b3

Вправа 8. Чи існує скінчений автомат, що допускає тільки слова мови з вправи 36 теми 4.1.

Вправа 9. Задати скінчений автомат, що допускає мову, визна­чену регулярним виразом:

1. (0+1) * 2 ;

2. (0+1) * (2)* ;

3. ( 0 1) * 2 + (0+1) * 2 ;

4) ( 0 2) * 3 (2)* + ( 10(2) * + 1(2)*) 2 (0) *;

5) (1)* 2 (3)* + ((1) * 0 + 12 (3)*) 2;

6) 12 (3)* + 3 (0)* (2 (1) * + ( 12) * );

7) 10 ( 10)* (2 (3) * + 02) + 2 ( 3) * ( 0+ 2) * + 2 (3 +0);

8) ( 10) * ( 2 + (3) *) + 1 ( 2) * ( 2+ (3) *) + 12 (( 1) * + 10) *;

9) ( 2 + 3) * ( 10) * + 12 ( 0) * + ( 1) * 2 ( 3)* ;

10) 1 ( 1) * + ( 2 + 0) * ( 1)* + ( 2 + 0) * + 1 ( 0) *.

Приклад: Задамо скінчений автомат, що допускає мову, визначену регулярним виразом

AБ (A) * ( Б + B) * + (A Б) * BГ * + Б * ( В + Г) * .

П о-перше, представимо регулярний вираз у вигляді орграфу, для чого операції об’єднання поставимо у відповідність розгалуження ребер, операції конкатенації - послідовність ребер, операції ітерації - петлю. Але у цьому випадку утворюються хибні шляхи, а звідси можливі слова, які не належать до регулярної множини, визначеної початковим регулярним виразом. Такими словами, наприклад, є слова ВБАБВГ, ГВАББВ та ін. Тому використовуємо правила усування хибних послідовностей. Спочатку введемо порожні стрілки, щоб звільнитися від утворення хибних послідовностей, які виникають за рахунок ітерації, що брали участь у конкатенації зліва, причому конкатенації пов’язані об’єднанням. Але і в цьому випадку ще можливе утворення хибних послідовностей, наприклад ГГВВББ.

Введемо порожні стрілки, щоб звільнитися від хибних послідовностей, обумовлених конкатенацією ітерації. Легко встановити, що хибні послідовності у графі не виникають.

По-друге, звернемося до алгоритму абстрактного синтезу автоматів. Домовимося, що скінчений автомат зображує появу допустимого слова вихідною буквою Д.

Проводимо переіндексацію вершин графу, приписуючи індекс вершини, з якої виходить порожня стрілка, зліва до індексу вершини, куди ппрожня стрілка входить.

Таким чином, граф має такий вигляд:

Побудуємо за допомогою цього графу таблицю переходів (зірочка у стовпцях 4 + 5, 5 таблиці означає, що вихідний символ з’являється на виході автомату тільки після вхідних символів Б або В).

Задамо переіндексацію станів автомату функцією f: I*  I такого вигляду:

f = {(1,1), (2+6, 2), (8,3), (7+9,4), (9,5), (3+5, 6),(3+6,7), (4,8), (4+7,9),(3,10), (4+5,11),(7,12), (6,13), (5,14)} .

Вхід	Вихід
	-	Д	Д	Д	Д	Д
	Індекс
	1	2+6	8	7+9	9	3+5
А	2+6	-	-	-	-	3+6
Б	8	3+5	8	-	-	4
В	7+9	-	9	9	9	4+7
Г	9	-	9	7+9	9	-

Вхід	Вихід
	Д	Д	Д	Д	Д*	Д	Д	Д*
	Індекс
	3+6	4	4+7	3	4+5	7	6	5
А	3	-	-	3	6	-	-	6
Б	4+5	4	4	4	4	-	5	-
В	4	4	4	4	4+7	-	-	7
Г	-	-	7	-	-	7	-	-

Це спрощує позначення станів, і граф переходів синтезованого автомату набуває вигляду:

Легко переконатися, що синтезований скінчений автомат допускає тільки слова мови, заданої регулярним виразом АБ(А)* (Б+В)* + (АБ)* ВГ*+ Б* (В+Г)*.

Вправа 10. Задати скінчений автомат, що допускає мову, визначену регулярним виразом:

І) 20((1)*2+(1)*3(0)*)+(20)*0(1)*;

2) 1(0)*(2(1)*(3)*+(01)*(3)*)+2(01)*;

3) 3(1+3)*+(01)*(1+3)*+20(1+2+3)*;

4) 10(2)*+(10)*(2+3)+(1+2+3)*0(1)*;

5) (2)*1(3)*+(0)*2(3)*+(0+1+2)*0(3)*;

6) (1+2)*0(1+2)*+3(0)*((1+2)*+01(2)*);

7) (2+3)*(01(2)*+(10)*3)+01(2)*10(2+3)*;

8) (3+2+1)*0(1+2)*1+01(2)*(1+2)*;

9) (1+2)*0(2+3)*+(1)*02+(0+1)*02;

10) (2+(2)*)*+3(0)*2+1(2)*((3)*+(01)*);

11) (1+2)*3(0)*+(2+3)*3(0)*+(2+0)*3(0)*;

12) (2+0)*0(3+1)*+(0)*(1(23)*+3(2)*);

13) (0+1)*(01)*+(0)*(1)*(01+10);

14) 012+123+(0)*((12)*+(13)*);

15) (21)*(2+1)*+(010)*(2+(3)*);

16) 1(1)*2(2)*+(2)*3+(2)*10+(10)*2;

17) 2(1)*(0(1)*+02(1)*+3(1)*)+2(1)*3.

Вправа 11. Заданий скінчений автомат M = < E, А, В, f₁, f₂ >, де Е = {0,1} - множина вхідних символів, А = {a₀, a₁, a₂} - множина станів, {В,Ч,H} - множина вихідних символів, f₁ - функція переходів, f₂ - функція виходів:

f₁(a₀ ,0) = a₁; f₁(a₁ ,1) = a₂; f₁(a₂ ,0) = a₁;

f₁(a₀ ,0) =Ч; f₁(a₁ ,1) =H; f₁(a₂ ,0) =Ч;

f₁(a ₁,0) =a₁; f₁(a₀ ,1) =a₂; f₁(a₂ ,1) =a₂;

Необхідно:

1) описати поведінку автомату в часі;

2) встановити вихідну послідовність, якщо на вхід автомата, який знаходиться у стані α₀, буде подана така вхідна послідовність: а) 0010; б) 1111; в) 00000; г) 10100;

3) встановити вхідну послідовність, здатну перевести автомат із стану α₀ в стан α₁ через стан α₂;

4) встановити математичну властивість двійкових чисел, яку встановлює автомат.

Вправа 12. Скінченний автомат заданий таблицею переходів:

	ai+1		bi
	0	1	0	1
a1	a1	a3	0	1
a2	a7	a6	0	1
a3	a4	a3	0	1
a4	a3	a4	0	1
a5	a2	a4	0	1
a6	a2	a5	0	1
a7	a2	a6	1	1

Поставити діагностично безумовний експеримент для таких пар станів:

1) a₂ та a₁; 2) a₂ та a₃; 3) a₃ та a₆;

4) a₁ та a₅; 5) a₃ та a₄; 6) a₅ та a₆;

7) a₁ та a₃; 8) a₁ та a₇.

Приклад 1: Побудуємо розрізняючу послідовність для пари станів (a₅, a₆). Будуємо послідовність таблиць П_i, доки стани a₅ i a₆ не стануть розрізненими, або не буде ясно, що вони еквівалентні.

П1

П2

П3

П4

0

1

0

1

0

1

0

1

a1

a11

a31

1

a1

a41

a31

1

a1

a41

a31

1

a1

a41

a31

1

a2

a72

a61

a2

a41

a31

a2

a41

a31

a2

a41

a31

a3

a41

a31

a3

a31

a41

a3

a31

a41

a3

a31

a41

a4

a31

a41

a4

a22

a41

a4

a23

a41

2

a4

a24

a41

2

a5

a21

a41

a5

a22

a51

a5

a23

a52

a5

a24

a52

3

a6

a21

a51

a6

a13

a61

2

a6

a14

a62

3

a6

a75

a63

4

a7

a21

a61

2

a7

a21

a61

3

a7

a23

a62

4

a7

a24

a63

5

При переході від табл. П₃ до П₄ стани а₅ та а₆ розійшлися.

Знаходимо у табл. П₃ стовпець, у якому верхні індекси у рядках а₅ та а₆ різні. Це стовпець 1. Таким чином, перший символ розріз­няючої послідовності - 1. Вибираємо в табл. П₃ стани на перетині стовпця 1 та рядків а₅ та а₆. Це стани а₄ та а₅ . У табл. П₂ знаходимо стовпець, у якому верхні індекси у рядках а₄ та а₅ різні. Це стовпець 0. Таким чином, другий символ розрізняючої послідовності - 0. Виберемо у табл. П₂ стани на перетині стовпця 0 та рядків а₄ та а₅. Це стани а₂ та а₃.

У табл. П₁ знаходимо стовпець, у якому верхні індекси у ряд­ках а₂ та а₃ різні. Це стовпець 0. Таким чином, третій символ розрізняючої послідовності - 0.

Вибираємо у табл. П₁ стани на перетині стовпця 0 та рядків а₂ та а₃. Це стани а₁ та а₄. У підтаблиці b_i таблиці переходів автомату знаходимо стовпець, у якому вихідні символи у рядках а₄ та а₇ різні. Це стовпець 0. Таким чином, останній символ послідовності 0, і вона має вигляд 1000.

Треба уникати таких помилок, які часто зустрічаються:

1) визначити перший символ послідовності за допомогою тієї табл. П_i, де стани пари вперше розійшлися (так, для нашого прик­ладу не можна визначати перший символ за табл. П₄);

2) вважати перший знайдений символ останнім символом розрізняючої послідовності, другий знайдений - передостаннім символом розрізняючої послідовності і т.д.

Друга помилка пов’язана з хибним уявленням про роботу алгоритму. Опишемо ще раз головну ідею алгоритму. Алгоритм “намагається” знайти той єдиний символ, при поданні якого на вхід автомату стани пари, що підлягає аналізу, можуть бути різні за виходом. Якщо такого символу немає, тоді алгоритм намагається знайти такий символ, який дозволить перейти до аналізу іншої пари станів, по відношенню до яких автомат намагається знайти той єдиний символ, при поданні яко­го на вхід автомату ця пара станів може бути різна за виходом. Якщо й такого символу немає, тоді алгоритм робить спробу знайти такий символ, який дозволить перейти до такої пари станів, до якої алго­ритм намагається підійти так, як описано у попередньому абзаці, і т.д.

Тому перший знайдений символ є першим символом розрізняючої послідовності, другий - другим символом розрізняючої послідовності і т.д.

Приклад 2: Побудуємо розрізняючу послідовність для пари станів (а₃, а₄). Скористаємося побудованою послідовністю таблиць із розглянутого прикладу. Легко помітити, що у табл. П₄ немає рядків із різними верхніми індексами. Звідси робимо висновок про те, що табл. П₄ подає еквіва­лентне розбиття автомату. Оскільки а₃ та а₄ належать до однієї підмножини розбиття, то їх не можна розрізнити.

Вправа 13. Поставити діагностичний безумовний експеримент для пар станів:

І) а₁ і а₂ ; 2) а₁₁ і а₁₂ ; 3) а₃ і а₁₀ ; 4) а₁₂ і а₁₃ ;

5) а₁ і а₁₃ ; 6) а₄ і а₅ ; 7) а₁ і а₉ ; 8) а₂ і а₁₃ ;

9) а₁₁ і а₁₂ ; 10) а₈ і а₁₃ ; 11) а₅ і а₇ ; 12) а₁₁ і а₁₃

скінченого автомату, заданого такою таблицею переходів:

	ai+1		bi
	0	1	0	1
a1	a1	a2	0	1
a2	a1	a2	0	1
a3	a4	a5	1	1
a4	a6	a7	1	0
a5	a11	a12	1	0
a6	a9	a10	0	0
a7	a7	a1	1	0
a8	a1	a1	0	1
a9	a13	a9	0	1
a10	a5	a4	1	1
a11	a9	a11	0	1
a12	a8	a3	0	1
a13	a9	a13	0	1
a14	a9	a14	0	1

Вправа 14. Навести приклади скінчених автоматів із парами станів, що не розрізняються. Довести нерозрізнимість станів.

Вправа 15. При невідомому початковому стані скінчений автомат, наведений у вправі 2, на вхідну послідовність 1101 видав вихідну послідовність 1010. Визначити початковий стан скінченого автомату.

Вправа 16. Поставити діагностичний безумовний експеримент для пар станів:

І) а₁ і а₂ ; 2) а₃ і а₇ ; 3) а₁ і а₆ ; 4) а₁₅ і а₁₆ ;

5) а₄ і а₁₃ ; 6) а₂ і а₁₅; 7) а₄ і а₁₁ ; 8) а₈ і а₁₈

скінченого автомату, заданого такою таблицею переходів:

	ai+1		bi
	e1	e2	e1	e2
a1	a2	a3	0	1
a2	a1	a9	0	1
a3	a9	a6	1	0
a4	a11	a5	1	1
a5	a1	a6	1	0
a6	a1	a12	0	1
a7	a1	a14	0	1
a8	a4	a15	0	1
a9	a3	a7	1	0
a10	a1	a4	1	0
a11	a1	a13	1	1
a12	a14	a15	0	0
a13	a11	a16	1	1
a14	a12	a17	0	0
a15	a16	a16	0	1
a16	a15	a17	0	1
a17	a1	a11	1	0
a18	a2	a15	0	1

Вправа 17. Встановити пару станів скінченого автомату з вправи 5, діагностична послідовність для якої має більшу довжину з усіх пар розрізнимих станів цього автомату.

Вправа 18. Які переваги має кратний діагностичний експеримент перед простим діагностичним?

Вправа19. Поставити діагностичний безумовний експеримент для пар станів:

І) а₄ і а₁ ; 2) а₁ і а₉ ; 3) а₉ і а₁₁ ;

4) а₂ і а₁₂ ; 5) а₃ і а₁₀ ; 6) а₁ і а₇

скінченого автомату, заданого такою таблицею переходів:

	ai+1			bi
	e1	e2	e3	e1	e2	e3
a1	a7	a2	a7	b1	b2	b3
a2	a11	a12	a9	b1	b2	b2
a3	a1	a2	a5	b1	b1	b2
a4	a2	a1	a5	b1	b2	b3
a5	a7	a9	a7	b1	b2	b1
a6	a9	a7	a2	b2	b2	b1
a7	a7	a8	a4	b1	b2	b3
a8	a6	a7	a12	b3	b2	b3
a9	a5	a10	a5	b1	b2	b3
a10	a5	a9	a3	b3	b2	b3
a11	a1	a11	a9	b1	b2	b3
a12	a13	a8	a3	b1	b2	b3
a13	a3	a6	a1	b2	b2	b3

Вправа 20. Поставити діагностичний безумовний експеримент для пар станів:

І) а₁ і а₂; 2) а₆ і а₇; 3) а₁₁ і а₁₂; 4) а₁ і а₁₁;

5/ а₂ і а₁ ; 6/ а₅ і а₉ ; 7/ а₅ і а₁₃ ; 8/ а₆ і а₁₂

скінченого автомату, заданого такою таблицею переходів:

	ai+1			bi
	e1	e2	e3	e1	e2	e3
a1	a1	a2	a6	0	1	1
a2	a2	a1	a7	0	1	1
a3	a2	a13	a6	1	0	1
a4	a4	a2	a4	0	1	1
a5	a1	a6	a9	1	0	0
a6	a1	a2	a11	0	1	1
a7	a1	a3	a12	0	1	1
a8	a2	a7	a4	0	0	1
a9	a5	a13	a8	1	0	0
a1	a5	a13	a8	1	1	0
a11	a2	a6	a10	0	1	1
a12	a3	a7	a13	0	1	1
a13	a2	a7	a10	1	0	0

Вправа 21. Побудувати діагностично безумовний експеримент для пар станів:

І/ а₄ і а₆; 2) а₁ і а₂; 3) а₃ і а₄; 4) а₁ і а₈

скінченого автомату заданого у вправі 7 п. І.

Вправа 22. Побудувати діагностично безумовний експеримент для пар станів:

І) а₃ і а₉; 2) а₇ і а₁₁; 3) а₄ і а₉

скінченого автомату, заданого у п. 5 вправи 7.