2. Правила виведення.

(P1) Правило розширення: якщо A, то B  A;

(P2) Правило скорочення: якщо A  A, то A;

(P3) Правило асоціативності: якщо A  (B  C), то (A  B)  C;

(P4) Правило перетину: якщо A  B і 7A  C, то B  C;

(P5) Правило впровадження квантора існування: якщо A  B і B не має вільного входження x, то x(A B).

Визначення теорії першого порядку Т з рівністю.

Нехай визначена вище теорія першого першого порядку Т містить предикатний символ A₁². Далі будемо позначати A₁²(t,s) як t = s, і 7A₁²(t,s), як t  s. Теорія T , що містить цей нелогічний символ, буде називатися теорією першого порядку з рівністю, якщо вона містить у собі ще дві аксіоми:

(A6) x (x = x)

(A7) (x = y)  ( A(x, x)  A(x, y)) , де y вільне для x, а A(x, y) одержуємо заміною яких-небудь, але не обов'язково всіх, вільних входжень x на y у A(x, x).

Стосовно будь-якої теорії першого порядку можна стверджувати, щои вона є теорією першого порядку з рівністю, якщо такі формули є її теоремами:

T1. x_i (x_i = x_i ) - рефлексивність рівності;

T2. (x = y)  (A(x,x)  A(x,y)) - підстановочність рівності.

З цього означення теорії першого порядку з рівністю можна вивести декілька допоміжних теорем, зокрема:

a)├ t = t для будь-якого терму t (із теореми Т1, застосовуючи правило A4);

б) x = y  y = x.

Нехай A(x,x) є x = x, A(x,y) є y = x. Тоді, відповідно до теореми Т2, ├ (x = y)  (x = x  y = x). Проте вище було доведено, що x = x. Використовуємо тавтологію B  ((A  (B  C))  (A  C)) наступним чином (x = x)  ((x = y  (x = x  y = x))  (x = y  y = x)). Оскільки x = x, x = y  (x = x  y = x) вже виведені, то, застосувавши двічі правило MP, одержимо ├ x = y  y = x;

в) x = y  (y = z  x = z).

Нехай A(y,y) є y = z, A(y,x) є x = y. Тоді, відповідно до теореми Т2, одержуємо ├ y = x  (y = z  x = z). Згідно з пунктом б) ├x = y  y = x. Використовуємо тавтологію (A  B)  ((B  C)  (A  C)) наступним чином: (x = y  y = x)((y = x  (y = z  x = z))  (x = y  (y = z  x =z ))). Оскільки x = y  y = x - теорема, а y = x  (y = z  x = z) вже виведена, то застосувавши двічі правило MP, одержуємо ├ x = y  (y = z  x = z).

Теорема 1.

Нехай K - теорія першого порядку з рівністю, в якій до числа теорем належить теорема Т1, а також усі формули вигляду Т2, А(х,х) елементарна, не містить входжень функціональних літер, а А(x,y) утворюється з А(х,х) заміною на y точно одного входження х.

Крім того, для будь-якої функціональної букви f_j і для будь-якого набору змінних z_i,... , z_n ├ x=y f_j (z_i,... , z_n) = f_j (w_i,... , w_n), де f_j (w_i,... , w_n) отриманa з f_j (z_i,... , z_n) заміною деякого входження x на y. Тоді K - теорія першого порядку з рівністю.

Нехай К₁ - теорія першого порядку з єдиною предикатною літерою =, без функціональних літер і предметних констант, із власними аксіомами:

 x_i (x_i = x_i);

 x_i  x₂ ( x_i = x₂  x₂ = x_i);

 x_i  x₂  x₃ (x_i = x₂ ( x₂ = x₃  x_i = x₃)).

Рекомендується довести, що К₁ - теорія першого порядку з рівністю.

Примітка: в силу вище наведеної теореми, достатньо вивести наступні формули:

x=y(x=xy=x);

x=y(x=xx=y);

x=y(x=yy=y);

x=y(y=xy=y);

x=y(x=zy=z);

x=y(z=xz=y).

Приклади конкретних теорій першого порядку.

1. Визначимо теорію решіток R, виведемо в ній якусь теорему і приведемо інтерпритацію, в якій виведена теорема хибна.

Алгебра G = (A,W) називається решіткою, якщо її сигнатура W складається з двох бінарних операцій:  (inf, “нижня грань” ) і  (sup, “ верхня грань ”) , і для всіх x, y, zA виконуються умови:

1) xx = x, xx = x;

2) xy = yx, xy = yx;

3) (xy)z = x(yz), (xy)z = x(yz);

4) x(xy) = x, x(xy) = x.

Визначимо нелогічні символи теорії R: функціональні символи: f₁², f₁² (для операцій ,  відповідно); предикатна літера A₁² (для рівності “=”).

Визначимо нелогічної аксіоми в традиційній для решіток системі позначень:

(А1) xx = x, xx = x;

(A2) xy = yx, xy = yx;

(A3) (xy)z = x(yz), (xy)z = x(yz);

(A4) x(xy) = x, x(xy) = x;

(A5) x = x;

(A6) x = y  y = x;

(A7) x = y  (y = z  x =z );

(A8) x = y  (zy = zx);

(A9) x = y  (zy = zx).

Запишемо нелогічної аксіоми мовою теорії Т:

(A1) xA₁² (f₁²(x,x),x), xA₁² (f₂²(x,x),x);

(A2) xyA₁² (f₁²(x,y),f₁²(y,x)), A₁² (f₂²(x,y),f₂²(y,x));

(A3) xyzA₁² (f₁²(f₁²(x,y),z), (f₁²(x, f₁²(y,z))), xyzA₁² (f₂²(f₂²(x,y),z), (f₂²(x, f₂²(y,z)));

(A4) xyA₁² (f₁²(x,f₂²(x,y)),x), xyA₁² (f₂²(x,f₁²(x,y)),x);

(A5) xA₁² (x,x);

(A6) xy(A₁² (x,y)  A₁² (y,x);

(A7) xyz (A₁² (x,y)  (A₁² (y,z)  A₁² (x,z)));

(A8) xyz (A₁² (x,y)  (A₁² (f₁²(z,y),f₁²(z,x)));

(A9) xyz(A₁² (x,y)  (A₁² (f₂²(z,y),f₂²(z,x))).

Виведемо формулу: ((xy)((xy)x))y = y

(xy)((xy)x = xy -аксіома (A4);

xy = yx - аксіома (A2);

(xy)((xy)x) = xy  (xy = yx  (xy)((xy)x) = yx - аксіома (A7);

xy = yx  (xy)((xy)x) = yx за МР із 1),3);

(xy)((xy)x) = yx за МР із 2),4);

(xy)((xy)x) = yx  (y(yx) = y((xy)((xy)x))) - аксіома (A9);

y(yx) = y((xy)((xy)x)) за МР із 5) і 6);

y(yx) = y((xy)((xy)z))  y((xy)((xy)x)) = y(yx) - аксіома (A6);

y((xy)((xyz)) = y(yx) за МР із 7) і 8);

y(yx) = y -аксіома (A4);

y((xy)((xy)x)) = y(yx)  (y(yx) = y  y((xy)((xy)x)) = y -аксіома (A7);

y(yx) = y  y((xy)((xy)x)) = y за МР із 9) і 11);

y((xy)(xy)x)) = y за МР із 10) і 12);

((xy)((xy)x))y = y((xy)((xy)x)) -аксіома (A2);

((xy)((xy)x))y = y((xy)((xy)x))  (y((xy)((xy)x)) = y  ((xy)((xy)x))y - аксіома (A7);

y((xy)((xy)x)) = y  ((xy)((xy)x))y = y за МР із 14) і 15);

((xy)((xy)x))y = y за МР із 13) і 16).

Інтепретація, в якій виведена теорема хибна:

область інтерпретації: D = N - множина натуральних чисел;

функції інтепретуємо операціями додавання (для f₁²) і множення (для f₂²);

предикат A₁² інтепретуємо відношенням рівності.

2. Визначимо теорію H частково впорядкованих множин, виведемо в ній якусь теорему і наведемо інтепретацію, в якій виведена теорема набуває хибного значення.

Частково впорядкована множина має наступні властивості:

рефлексивність x  x;

антисиметричність x  y, y  x  x = y;

транзитивність x  y, y  z  x  z,

де  - відношення часткового впорядкування.

Визначимо нелогічні символи теорії H:

A₁² - для відношення часткового порядку ;

A₂² - для рівності “=”.

Визначимо нелогічні аксіоми теорії H в мові теорії Т:

(G1) xA₁²(x,x);

(G2) xy(A₁² (x,y)  (A₁² (y,x)  A₂² (x,y)));

(G3) xyz (A₁² (x,y)  (A₁² (y,z)  A₁² (x,z)));

(G4) xA₂²(x,x);

(G5) xy (A₂² (x,y)  A₂² (y,x));

(G6) xyz (A₂² (x,y)  (A₁² (y,z)  A₁² (x,z))).

Виведемо формулу xy(A₁² (x,y)  (A₂² (x,y)  (A₁² (y,x)  A₂² (x,y))).

A₁² (x,y) - гіпотеза;

xy(A₁² (x,y)  (A₁² (y,x)  A₂² (x,y))) - аксіома (G2);

xy(A₁² (x,y)  (A₁² (y,x)  A₂² (x,y)))  y(A₁² (x,y)  (A₁² (y,x)  A₂² (x,y))) - аксіома (A4);

y(A₁² (x,y)  (A₁² (y,x)  A₂² (x,y))) - за МР із 2) і 3);

y(A₁² (x,y)  (A₁² (y,x)  A₂² (x,y)))  (A₁² (x,y)  (A₁² (y,x)  A₂² (x,y))) - аксіома (A4);

(A₁² (x,y)  (A₁² (y,x)  A₂² (x,y))) - за МР із 4) і 5).

Таким чином, формула (A₁²(x,y)  (A₁²(y,x)  A₂²(x,y))) виводиться в H. Використовуючи відому властивість виводу, можемо записати (A₁²(x,y)  (A₁²(x,y)  (A₁²(y,x)  A₂²(x,y))). Звідси за теоремою дедукції отримаємо: (A₁² (x,y)  (A₁² (x,y)  (A₁² (y,x)  A₂² (x,y))). Двічі застосувавши правило Gen, одержимо:

xy (A₁² (x,y)  (A₁²(x,y)  (A₁²(y,x)  A₂²(x,y))).

Наведемо інтепретацію, в якій дана формула хибна:

1) область інтепретації D = {a,b,c,d};

2) предикат A₁²(x,y) інтерпретуємо відношенням R₁= {(a,b),(a,c),(b,a),(c,d),(a,c)};

3) предикат A₂²(x,y) інтерпретуємо відношенням R₂ = {(c,d),(a,c),(b,c),(a,a),(d,b)}.

Формула замкнена. При підстановці замість x і y об’єктів a і b відповідно, формула в області дії кванторів набуває хибного значення. Значить, на даній інтепретації формула хибна.

3. Визначимо теорію М моноїдів і виведемо в ній якусь формулу.

Моноїдом називається алгебраїчна система з однією бінарною операцією, щодо якої виконуються властивості асоціативності і існування одиниці.

Визначимо нелогічні символи: константа а₁ (для одиниці u); функціональний символ: f₁² (для операції); предикатна літера A₁² (для відношення рівності).

Визначимо нелогічної аксіоми в традиційних для алгебраїчних систем позначеннях:

(M1) x (y  z) = (x y) z;

(M2) x  u = x, u  x = x;

(M3) x = x;

(M4) x = y  y = x;

(M5) x = y  (y = z  x = z);

(M6) x = y  (z  y = z  x).

Визначимо нелогічної аксіоми в мові теорії Т:

(M1) xyzA₁² ((f₁²(x, f₁²(y,z)),f₁²(f₁²(x,y),z));

(M2) xA₁² (f₁²(x, а₁),x), xA₁² (f₁²(а₁,x),x);

(M3) xA₁²(x,x);

(M4) xy (A₁² (x,y)  A₁² (y,x));

(M5) xyz (A₁² (x,y)  (A₁² (y,z)  A₁² (x,z)));

(M6) xyz (A₁² (x,y)  (A₁² (f₁²(z,y), f₁² (z,x)))).

Виведемо формулу x  (y  u) = x  y.

x  (y  u) = (x  y)  u - аксіома (M1);

(x  y) u = x  y аксіома (M2);

x  (y  u) = (x  y)  u  ((x  y)  u = x  y  x  (y  u) = x  y) - аксіома (M5);

(x  y)  u = x  y  x  (y  u) = x  y - за МР із 1) і 3);

x  (y  u) = x  y - за МР із 2) і 4).

Подальший матеріал теми має ключове значення з погляду інженерної реалізації логіко-математичних формалізмів із метою їхнього застосування для вирішення практичних задач. Тому необхідно, проаналізувавши переваги і недоліки відомих підходів до вирішення проблеми характеризації, детально дослідити схему Ербрана і реалізацію її окремих кроків. Набудьте навичок побудови ербранівських універсуму і базису, повних семантичних дерев, застосування ознак суперечливості. Варто використовувати накопичений досвід зведення довільних формул логіки предикатів до скулемівської стандартної форми. Сполучайте практику побудови визначених схемою Ербрана конструкцій із глибоким обгрунтуванням коректності схеми Ербрана і реалізації її окремих кроків. У процесі побудови повних семантичних дерев намагайтеся обмежитися їхніми найменшими піддеревами, що дозволяють встановити суперечливість множини диз'юнктів, що розглядається.

Сутність підходів Гіллмора, Девіса і Патнема варто аналізувати не тільки в історичному аспекті, але й у плані формування стрункої системи і методики доведення теорем.

Найбільш повне уявлення про метод резолюцій Робінсона дає інтеграція концепцій узагальнення підходу Девіса і Патнема (їхнього другого правила) і доведення повноти методу на основі переходу від закритого повного семантичного дерева до суперечливої множини основних прикладів диз'юнктів.

Уніфікацію рекомендується розглядати як певне правило зведення диз'юнктів і основних прикладів диз'юнктів до зручного для застосування правила резолюцій вигляду.

Метод насичення і стратегію викреслювання варто розглядати як базові концепції машинної реалізації підходу Робінсона, що враховують алгоритмічний характер процесів, що програмуються, і прагнення до ефективності.

Модифікації методу резолюцій необхідно розглядати в плані поглиблення уявлень про інженерні методи доведення теорем. Доцільно розглядати існуючі модифікації методу резолюцій із точки зору на доведення як комбінаторний процес. Важливо сформувати уявлення про пошуковий простір, базові концепції пошуку в глибину та в ширину тощо. Потім переходьте до стратегій модифікації методу резолюцій як комбінацій універсальних методів скорочення перебору: впорядкування, розбиття і використання спеціальних графічних структур.

Дослідіть семантичну і ЛОК резолюції, лінійний і впорядкований лінійний виводи. Зверніть увагу на значення вдалого вибору впорядкування літер і диз'юнктів, індексації, розбиття для ефективності модифікацій, що розглядаються.

Значення клаузальних форм логіки теми визначається роллю логіко-математичних числень у теорії штучного інтелекту. Реалізація традиційного погляду на проблему як формулу, що потребує доведення, а на аксіоми і правила виводу як на засоби побудови виводів, в умовах застосування числень гільбертовського типу наштовхнулася на серйозні перешкоди.

Ці числення виявилися не дуже зручними з погляду людини, що вирішує проблеми, тому що не дозволяли природно подавати проблеми і варіанти їхньої декомпозиції на підпроблеми, відзначати підпроблеми, що мають рішення. З іншого боку, ці числення не можна було покласти в основу створення мов логічного програмування.

Тому були розроблені генценівські (секвенціальні) варіанти числень і теорій першого порядку. Рекомендується почати аналіз мови секвенціальних числень з аналізу секвенцій. Потім варто усвідомити значення другої специфічної особливості секвенціальних числень: наявність великого числа правил виведення за умови використання єдиної схеми аксіом. Набудьте навичок побудови виводів в численні предикатів LK і переходьте до аналізу його дедуктивних властивостей.

З погляду практики нас влаштовують секвенції не довільного вигляду, а тільки секвенції спеціального вигляду, що відомі як клаузи Хорна. Рекомендується дослідити особливості представлення знань у вигляді клауз Хорна, набути відповідних навичок, засвоїти алгоритм переходу від стандартної до клаузальної форми логіки.

На завершення проаналізуйте метод резолюцій для клаузальної логіки та його модифікації, зокрема резолюцію на графах з'єднань.

Насамкінець рекомендується розглянути ще один підхід до доведення теорем, побудований на ідеях реалізації алгебраїчного методу. Формальним апаратом цього підходу є термопереписуючі системи.

Варто усвідомити сутність термопереписуючої системи та еквівалентність механізмів редукції термів r,s в термопереписуючій системі і виведення формули r=s у відповідній теорії першого порядку з рівністю. Дуже важливо зрозуміти й оцінити практичну користь таких властивостей канонічної термопереписуючої системи як нетеровість і конфлюентність. Потрібно достатнє вміння використання процедур зведення довільної термопереписуючої системи до канонічного виду.

На закінчення рекомендується вивчити канонічну термопереписуючу систему для числення висловлювань і навчиться її застосувати на практиці.

Вправи до теми 6.3.

Вправа 1. Встановити можливість використання наслідків 1 та 2 теореми дедукції Ербрана, встановлених для числення висловлювань L, при виведенні теорем логіки предикатів.

Вправа 2. Вивести в теорії першого порядку Т1 такі формули:

1. (x(AB) (xAxB));

2. x(AB)xAxB;

3. x(AB)~xAxB;

4. x(A&B)xA&xB;

5. 77xАxА;

6. xА77xА;

7. (7xA7xB)(xBxA);

8. (xAxB)(7xB7xA);

9. xA77xAxA;

10. xAxA;

11. xA&xBx(A&B);

12. xAxBx(AB);

13. xyAyxA;

14. xyAyxA;

15. xyAyxA;

16. (xAxB)xA;

17. xBxBxB;

18. xA(xBxA);

19. xAxBxAxB;

20. xAxB(xC(xAxB));

21. ((xAxC)(xCxD))(xAxD);

22. xA(x)Bx(A(x)B);

23. xA(x)xB(x)x(A(x)B(x));

24. x(A(x)B(x))xA(x)xB(x);

25. xAx7A7xA;

26. x(A(x)B)xA(x)B;

27. xA(xAxB);

28. xAyBxCx7C;

Приклади виконання вправи.

Приклад 1. Виведемо xA(xBxA).

Запишемо формулу через зв’язки  і 7 у вигляді 7xA(xBxA).

1. 7xAxA - пропозиціональна аксіома (А1);

2. 77xAxA - пропозиціональна аксіома (А1);

3. xA7xA - правило перетину Р4 з формул 1,2;

4. 7xB(xA7xA) - правило розширення для формули 3;

5. (7xB xA)7xA - правило асоціативності для формули 4;

6. 7(7xB  xA) (7xB  xA) - пропозиціональна аксіома (А1);

7. 7xA(7xB xA) - правило перетину Р4 із формул 5,6.

Зауважимо, що правило перетину, застосоване до формул 5,6, дозволило поміняти місцями праву і ліву частини формули 5 щодо зв’язки . Використовуючи гіпотези і теорему Ербрана, вивід даної формули можна значно спростити:

1. xA - гіпотеза;

2. 7xB  xA - правило розширення для формули 1;

3. xB xA - запис зв’язки  через ;

Застосувавши теорему Ербрана до 1,3, одержимо ├ xA(xBxA).

Приклад 2. Виведемо 77АА.

Запишемо формулу через зв'язки  і 7:

777АА.

Будемо використовувати вивід в оберненому напрямку (рух від результату до аксіом). Спробуємо одержати дану формулу за допомогою правила перетину, для цього достатньо у висновку мати формули:

1. x777A;

2. 7xA;

Застосуємо до формули 2 схему пропозиційної аксіоми (А1), тоді вона буде мати вигляд 7АА, а формула 1 - А777А за допомогою правила перетину (Р4), для цього необхідно у виводі мати формули:

3. yA;

4. 7y777A;

Аналогічно, застосувавши до формули 3 пропозиційну аксіому (А1), формула 3 приймає вигляд 7АА, а формула 4: 77А777А. Будуємо вивід формули 4 аналогічним способом, припускаючи, що вона отримана після застосування правила перетину. Для цього необхідно мати формули:

5. z77A;

6. 7z777A;

Якщо замість z підставити 777А, то до формул 5 і 6 може бути застосована схема пропозиційної аксіоми (А1).

Для наочності побудуємо дерево виводу:

AA

проп.акс(А1)

Приклад 3. Виведемо (АВ)(xAxB).

1. 7Ax7A аксіома підстановки;

2. 77Ax7A запис зв'язки "" через "" для формули 1;

3. 7AA пропозиціональна аксіома;

4. Ax7A правило перетину для формул 2,3;

5. x7AA правило перетину для формул 3,4;

6. 77x7A7x7A пропозиціональна аксіома;

7. 777x7A77x7A пропозиціональна аксіома;

8. 7x7A77x7A правило перетину для формул 6,7;

9. A77x7A правило перетину для формул 5,8;

10. 77x7AA правило перетину для формул 9,3;

11. 7x7AA запис зв'язки "" через "" для формули 10;

12. xAA oзначення -квантора;

13. ├ AB гіпотеза;

14. xAB наслідок 1 теореми Ербрана з формул 12,13;

15.  xAxB - правило введення -квантора у формулу 14.

Таким чином, AB|-xAxB. Звідси, за теоремою дедукції з формул 13,15 (АB)(xAxB).

Існують додаткові правила, що спрощують вивід. Наведемо деякі з них:

. Правило -введення.

Якщо АВ і х не є вільною змінною в А, то АxB.

Доведення:

1. ├ AB гіпотеза;

2. 7AB запис зв'язки "" через "" для формули 1;

3. 77A7A пропозиціональна аксіома;

4. B 7A правило перетину для формул 2,3;

5. 77B7B пропозиціональна аксіома;

6. 777B77B пропозиціональна аксіома;

7. 7B77B правило перетину для формул 5,6;

8. 7A77B правило перетину для формул 4,7;

9. 77BA правило перетину для формул 3,8;

10. 7B7A запис зв'язки "" через "" для формули 9;

11. x7B7A правило -введення;

12. 7x7B7A запис зв'язки "" через "" для формули 11;

13. 77x7B7x7B пропозиціональна аксіома;

14. 7A7x7B правило перетину для формул 5,8;

15. A7x7B запис зв'язки "" через "" для формули 14;

16. AxB введення -квантора.

З 1-16 можемо записати АB├ AxB (х не є вільною в А за умовою).

. Правило дистрибутивності для -квантора.

Якщо АB, тo xAxB.

Доведення наведене у прикладі 3.

Існує аналогічне правило для -квантора.

. Правило комутативності зв'язки "".

Якщо АВ, то ВА.

Доведення:

1. AB гіпотеза;

2. AA пропозиціональна аксіома;

3. BA правило перетину для формул 1,2.

З 1-3 можемо записати АВ├ ВА.

Приклад 4. Виведемо АВxAxB.

1. AB гіпотеза;

2. AA пропозиціональна аксіома;

3. AA запис зв'язки "" через "" для формули 2;

4. AxA правило -введення для формули 3;

5. AxA запис зв'язки "" через "" для формули 4;

6. BxB правило перетину для формул 1,5;

7. BB пропозиціональна аксіома;

8. BB запис зв'язки "" через "" для формули 7;

9. BxB правило -введення;

10. BxB запис зв'язки "" через "" для формули 9;

11. xAxB правило перетину для формул 6,10;

Таким чином, АBxAxB. Звідси |-АBxAxB за теоремою Ербрана.

Рекомендується побудувати в якості вправи вивід для таких формул:

1. x(AB)(xAxB);	6. xyA ~ yxA;
2. x(AB)~xAxB;	7. AB(xAxB);
3. xAxBx(AB);	8. xAA;
4. xyA ~ yxA;	9. (xAxB) xB;
5. x(AB) (xAxB);	10. (xBxA)( xAxB).

Вправа 3. Вивести в теорії першого порядку Т такі формули:

(x1A1(x1)x1A2(x1))((x1(A1(x1)) A2(x1)));	x(A~B)(xA~xB);
x(AB)(xAxB);	A├xA,А-замкнута;
xA(x)xA(x);	xAxB(xC(xAxB));
x(AB)(xAxB);	(AB)(BA);
x(AB)(xAxB);	x(AB)(xAxB);
xy(А(x)~А(y));	x(AB)xAxB;
x(AB)~xAxB;	x(A(x)B)xA(x)B;
x(AB)xAxB;	xAxB~xBxA;
AC,BD,AB├CD;	xAxA;
AxA;	xAxAxB;
xAA;	xyz(((A(x)A(y))(A(y)A(z))(A(z)A(x)))(A(z)~A(x)));
xA~xA;	xyz((A(x)A(y))~A(x)A(z));
xA~xA;	xy((A(x)~A(y))(A(x)~A(y)));
x(AB~BA);	A(x)B(x)x(A(x)B(x));
xAxBx(AB);	xy((A(x)~A(y))(A(x)~A(y)));
xyA~yxA;	xy(xy~xy);
xyA~yxA;	xyz((x~y)(x~z));
(xAxB)(xAxB);

Приклади виконання вправи.

Приклад 1. Виведемо ├ x A~xA.

Запишемо формулу у виді ((xAxA)(xAxA)) (використовуючи те,що A~B=((AB)(BA)) і xA=xA).

1. xAxA - теорема (частковий випадок теореми числення висловлювань AA);

2. xAxA - теорема (частковий випадок теореми числення висловлювань AA);

3. ( xAxA)((xAxA)(( xAxA)( xAxA))) -

теорема (частковий випадок теореми числення висловлювань A(B(AB)));

4. ├ (xAxA)(( xAxA)( xAxA)) - за правилом виводу MP із формул 1,3;

5. (xAxA)(xAxA) - теорема;

6. ├ (xAxA) - за правилом виводу MP із формул 2,5;

7. ├ ((xAxA)(xAxA)) - за правилом виводу MP із формул 6,7.

Теорема виведена.

У цьому прикладі був продемонстрований природний вивід у прямому напрямку. Приведемо приклад побудови виводу в зворотньому напрямку:

Приклад 2. Виведемо A(AB).

Для виводу даної формули можна вивести формули Ax і x(AB), а потім застосувати наслідок 2 теореми дедукції. Тепер потрібно визначити x. Нехай замінимо x на (BA) . Тоді A(BA) - аксіома (A1), а формула (BA)(AB) - відома теорема числення висловлень. Таким чином, одержуємо послідовність, що представляє вивід:

1. A(BA) - аксіома (A1);

2. (BA)(AB) - теорема числення висловлень.

3. A(AB) по наслідку 2 теореми дедукції.

Наведемо приклад виводу з гіпотезами:

Приклад 3. Виведемо A(t)├ xA(x), де терм t вільний для x у A.

1. A(t) - гіпотеза;

2. xA(x)A(t) - аксіома (A4);

3. (xA(x)A(t))(A(t)x(x)) - частковий випадок теореми числення висловлювань (DC)(CD);

4. A(t)xA(x) - за правилом виводу MP із формул 2,3;

5. A(t)├ xA(x) - за правилом виводу MP із формул 1,4.

Оскільки xA(x) еквівалентно xA(x), то одержимо, що A(t)├ x(x).

Слід зазначити, що для замкнених формул можна встановити ряд додаткових метатеорем, зокрема:

1. |-AxA;

2. |-xAA;

3. |-x(AB)(AxB);

4. |-x(BA)(xBA), якщо А і В - формули, до того ж у формулі А змінна х не є вільною.

Продемонструємо вивід деяких із них.

. Виведемо теорему AxA.

1. A - гіпотеза;

2. A├ xA - правило Gen;

Тоді за теоремою дедукції (оскільки формула А - замкнена щодо х, то теорема дедукції справедлива) одержуємо ├ AxA.

Відмітимо, що за аксіомою (A4) ├ xAA , тому автоматично одержуємо, що A~xA.

. Виведемо теорему x(AB)(AxB).

1. x(AB) - гіпотеза;

2. A - гіпотеза;

3. x(AB)(AB) - за аксіомою (A4);

4. AB - за правилом виводу MP із формул 1,3;

5. B - за правилом виводу MP із формул 2,4.

Тоді x(AB), А├ B.

Застосувавши правило Gen, одержимо x(AB), А├ xB.

Двічі застосувавши теорему дедукції одержимо вихідну формулу.

В якості вправи пропонуємо вивести наступні правила:

1. A,B├ A&B - правило кон'юнкції;

2. AC,BQ,AB├ CQ - правило диз'юнкції.

Вправа 4. Вивести в теорії першого порядку Т з рівністю такі формули:

x(B(x)~y(x=yB(y));	xy(x=yB(x)B(y));
x(B(x)~y(x=y)B(y));	xy(x=y(B(x)B(y)));
x(B(x)y(x=yB(y));	xy(x=y~(B(x)B(y)));
x(B(x)y(x=yB(y));	xy(x=y(B(x)~B(y)));
xy x=y;	xy(x=y~(B(x)~B(y)));
xy x=yyz(x=zx=yy=z);	xy(x=y(B(x)~B(y)));
xA(x)xy(A(x)A(y)x=y)~xy(x=y~~A(y));	xyz(xyyzzx~x=z);
xy(x=y(A(x)A(y)));	xyz(xyyzzxx=z);
xy(x=y(A(x)~A(y)));	xy(x~yx=y);
xyz(x=yx=zy=z);	xy(x=yx~y);
xyz(x=yy=z(A(x)A(z)));	xyz(x=y~x=zy=z);
xyz(x=yy=z(A(x)~A(z)));	xyz(x=yy=zA(x)~A(z));
xyz(x=zy=zx=y);	xyz(x=yy=zA(x)A(z));
xyz(x=zy=z~x=y);	xyz((A(x)~A(y))(A(y)~A(z))~x=z);
xyz(x=y(y=z(A(x)A(z))));	xyz((A(x)~A(y))y=z~x=z);
xyz(x=y(y=z(A(x)~A(z))));	xyz((A(x)~A(y))y=zx=z);
xy(x=y~(xy)(yx));	xy((x~y)~(x=y)).
xy(A(x)~A(y)x=y);

Приклади виконання вправи.

Продемонструємо вивід у даній теорії:

Приклад 1. Вивести x=y(A(x)~A(y)).

1. x=y(A(x)A(y)) теорема Т2 заміною A(x,x) на A(x) і A(x,y) на A(y);

2. x=yy=x симетричність рівності;

3. y=x(A(y)A(x)) теорема Т2;

4. x=y(A(y)A(x)) за наслідком 1 теореми дедукції;

5. x=y гіпотеза;

6. A(x)A(y) за правилом виводу MP із формул 5,1;

7. A(y)A(x) за правилом виводу MP із формул 5,3.

Таким чином, A(x)~A(y) за властивістю AB, BA ├ A~B.

Застосувавши теорему дедукції, одержимо ├ x=y(A(x)~A(y)).

Приклад 2. Вивести x(B(x)y(x=yB(y)).

1. B(x) гіпотеза;

2. x=y гіпотеза;

3. x=y(B(x)B(y)) теорема Т2 заміною A(x,x) на A(x) і A(x,y) на A(y);

4. B(x)B(y) за правилом виводу MP із формул 2,3;

5. B(y) за правилом виводу MP із формул 1,4.

Таким чином, B(x),x=y|-B(y).

Звідси B(x) ├ x=yB(y) за теоремою дедукції.

B(x)├ y(x=yA(y)) за правилом Gen.

Застосовуючи теорему дедукції і правило Gen, одержимо: ├ x(B(x)y(x=yB(y)).

Приклад 3. Вивести  x_iA(x_i) x₃ x₂ (A(x₃)А(x₂)( x₃ = x₂)) ~  x_i x₂ (x_i = x₂ ~A(x₂)).

Доведемо ряд допоміжних теорем (правил виводу).

Правило 1. A, B ├ AB.

Можна показати, що формула A(B(AB)) - теорема числення висловлювань.

Скоротивши запис за допомогою тотожніх перетворень, одержимо формулу A(BAB)).

Тепер побудуємо доведення для цього правила:

1. A(BAB));

2. A гіпотеза;

3. B гіпотеза;

4. ВАВ за правилом МР із 1 і 2;

5. АВ за правилом МР із 3 і 4.

Таким чином A, B ├ AB.

Правило 2. A, B ├ A~B.

1. A гіпотеза;

2. B гіпотеза;

3. A(BA) аксіома (А1);

4. BA за правилом виводу MP із формул 1,3;

5. B(AB) аксіома (А1);

6. AB за правилом виводу MP із формул 2,5;

7. (AB)(BA) за правилом 1.

Тоді A, B ├ A~B.

Тепер наведемо вивід основної формули:

1. x₃ = x₂ гіпотеза;

2. x_i = x_i гіпотеза;

3. A(x_i) гіпотеза;

4. A(x₂) гіпотеза;

5. A(x₃) гіпотеза;

6. (x₃ = x₂)(A(x₃)A(x₂)( x₃ = x₂)) аксіома (А1);

7. A(x₃)A(x₂) (x₃ = x₂) за правилом виводу MP із формул 1,6;

8. A(x₁)A(x₃)A(x₂) (x₃ = x₂) за правилом 1 із формул 3,7;

9.  x₁x₂ ((x₁ = x₂)(A(x₂) (x₁ = x₂)) аксіома (А1);

10.  x₁x₂(A(x₂) (x₁ = x₂)) за правилом виводу MP із формул 2,9;

11.  x₁x₂(A(x₂) ((x₁ = x₂)A(x₂)) аксіома (А1);

12.  x₁x₂((x₁ = x₂)A(x₂₎) за правилом виводу MP із формул 4,11;

13.  x₁x₂(A(x₂)  (x₁ = x₂)) ((x₁ = x₂)A(x₂)) за правилом 1 із формул 10,12;

14.  x₁A(x₁)x₃x₂(A(x₃)A(x₂)(x₃= x₂) ~ x₁x₂((x₁ = x₂)~A(x₂)) за правилом 2 із формул 8,13.

Слід зазначити, що головні концепції побудови виводу в теорії з рівністю залишаються в силі, оскільки ці теорії є лише розширенням теорії першого порядку. Отже, усі виведені в теорії першого порядку теореми зберігаються й у теорії першого порядку з рівністю.

Рекомендується в якості вправи побудувати вивід для таких формул:

1. x(B(x)~y(x=y&B(y));	3. xy(x=y);
2. x(B(x)~y(x=y&B(y));	4. xA(x)~xy(x=y~A(y)).

Вправа 5. Для формул логіки предикатів, заданих формулами логіки висловлювань і підстановками встановити чи є вони теоремами.

Варіанти формул числення висловлювань:

0 | A(AB)

1 | (AB)(BA)

2 | (AB)((AB)B)

3 | A(B(AB))

4 | ((AB)A)A

5 | (AB)(BA)

6 | A(A(BA))

7 | (A(BA))~((BA)A)

8 | (AB(B((AB)B))

9 | (AB)((AB)A)

Варіанти підстановки:

0. A=yx((A¹₁(x)A²₁(x,f(a)))(A²₁(x,y)A¹₁(y)));

B=xA¹₁(x)y(A²₁(y,f(a))x A²₂(x,y));

1. A=x(A¹₁(x) yA²₁(y,f²₁(a,x));

B=xyA²₁(x,y)A¹₁(a);

2. A=( A¹₁(a) xA²₁(x,a))y A¹₁(y);

B=xy A²₁(x,f(y))) A¹₁(a);

3. A=x (A¹₁(x) A²₁(x,f(a))yA³₁(x,y,a);

B=xy(A²₁(x,y)A²₂(x,a);

4. A=x A³₁(x,x,f(a))y A¹₁(y);

B=xy(A²₂(x,y) A³₁(x,y,f(a))) A¹₁(b);

5. A=xy(A²₁(x,y)_z(A²₁(y,z) A³₁(x,y,z)));

B=x A³₁(a,b,z)xy A²₁(x,y);

6. A=xyz(A³₁(x,b,f(z)) A³₂(c,y,f(b)));

B=xyz(A³₂(x,y,z) A³₁(x,y,f(z)));

7. A=x(A²₁(a,x)y A²₂(y,b));

B=xy(A²₂(y,x) A¹₁(x,y));

8. A=x(A²₁(x,x)_y A²₂(y,x));

B=xy(A²₂(y,x) A²₁(y,x));

9. A=xy A³₁(x,y,a);

B=x(A¹₁(x)(y A²₂(f(y),a)y A³₁(a,y,a))) A¹₁(b).

Формула логіки предикатів визначається підстановкою в формулу логіки висловлювань.

Теоретичні відомості з прикладом виконання завдання.

В цьому розділі використовуються структурні особливості формул для розв’язання проблеми характеризації. Встановлення логічної істинності формул розглядається як умова їхньої вивідності. Теоретичні основи автоматичного доведення теорем закладені Ербраном. Підхід Ербрана включає п’ять етапів. Перший з них полягає в переході від установлення логічної істинності формули до встановлення суперечливості її заперечення. В усіх методах доведення теорем розділу використовується не сама формула, а множина диз’юнктів її заперечення, яка й відбиває структурні особливості формули.

Для одержання множини диз’юнктів необхідно використовувати скулемівську стандартну форму (ССФ). Приведення формул до ССФ здійснюється у такій послідовності:

1) приведення формули до зведеної форми (якщо формула містить зв'язки: ~, , то необхідно перевести її до базису: , , , застосовуючи тотожності:

(*) A ~ B = (AB)(AB) або (AB)(AB);

(**) A  B = AB або (AB);

перенесення зв’язки  до елементарних формул здійснюється застосуванням правил де Моргана, властивостей подвійного заперечення та двоїстості кванторів:

xA(x) = xA(x), xA(x) = xA(x);

2. приведення формули до зведеної форми (формування префікса і матриці винесенням кванторів у початок формули шляхом застосування тотожностей:

а) Qx A[x]  B = Qx (A[x]  B), де формула B не містить x ;

б) Qx A[x]  B = Qx (A[x]  B), де формула B не містить x ;

в) x A[x]  x B[x] = x (A[x]  B[x]) ;

г)  x A[x]   x B[x] =  x (A[x]  B[x]) ;

д) Qx A[x]  Qx B[x] = Qx Qz (A[x]  B[z]) ;

е) Qx A[x]  Qx B[x] = Qx Qz (A[x]  B[z]) наведених вище властивостей двоїстості кванторів;

3) приведення матриці до КНФ шляхом застосування тотожностей булевої алгебри;

4) елімінування кванторів існування з префікса формули (якщо префікс містить квантор існування і ліворуч від нього немає кванторів загальності, то вводиться скулемівська константа, інакше - скулемівська функція, аргументами якої є змінні розташованих ліворуч кванторів загальності). При можливості має сенс спочатку виносити квантор існування і тоді ми можемо обійтися лише введенням нової константи, що демонструє наступний випадок:

x(x)y(y)	yx(A(x)B(y))x(A(x)B(c));
	xy(A(x)B(y))x(A(x)B(fc(x))).

Розглянемо декілька прикладів приведення формул до ССФ.

Приклад 1. Перетворимо до ССФ формулу (xA(x)yB(y))x(C(x)yB(y)).

Використовуючи лему 2.1, одержимо: xy(A(x)B(y))xy(C(x)B(y));

Перетворимо зв’язку  за формулою АB=АB: xy(A(x)B(y))xy(C(x)B(y));

Використовуючи властивості кванторів, одержимо: xy(A(x)B(y))xy(C(x)B(y)).

За лемою 2.1 одержимо: xy((A(x)B(y))xy(C(x)B(y))).

Використання правила де Моргана і властивостей дистрибутивності призводить до формули:

xy((A(x)B(y))xy(C(x)B(y))=xy(A(x)С(х)B(y)В(y)C(x)B(y)).

Тепер введемо скулемівські константи: (A(с₁)C(с₁)B(с₂))(B(с₂)C(с₁)B(с₂)).

Приклад 2. Перетворимо до ССФ формулу ((xАB)x(A(x)~B)).

За формулою АВ=(АВ) виконаємо перетворення формули до вигляду ((xАB)x(A(x)~B)).

Використовуючи лему 2.1 і властивості кванторів, отримаємо послідовно формули x(A(х)B)x(A(x)~B) і x((A(х)B)(A(x)~B)).

Оскільки А~B=ABAB, то

x((A(х)B)(A(x)B)(А(х)В))= x((A(х)B)(A(x)B)(А(х)В )).

Приклад 3. Перетворимо до ССФ формулу (x(x)(x(x)y(y)).

Використовуючи властивості кванторів, одержуємо (x(x)xy(A(x)B(y))), а формулу (x(x)xy(A(x)B(y))) - за лемою 2.1. Далі одержимо формулу (xА(x)y (A(x)B(y))) за лемою 2.1, а урахування властивостей кванторів призводить до xy(A(x)(A(x)B(y))). Звідси, за правилом де Моргана, одержимо формулу xy(A(x)A(x)B(y)), для видалення квантора  у якій введемо скулемівську константу: A(с₁)A(с₁)B(с₂).

Ербран запропонував доводити суперечливість формули, використовуючи систематичний перебір інтепретацій (без повторів і пропусків) за допомогою семантичних дерев, а в якості ознаки суперечливості формули обгрунтував існування для будь-якого її повного семантичного дерева скінченного закритого семантичного дерева. Дерево будується з використанням елементів ербранівського базису. Очевидно, що якщо у формулі є хоча б один функціональний символ, то ербранівський універсум і базис нескінченні, а значить і семантичне дерево може бути нескінченним. Наведемо приклад побудови фрагмента такого дерева.

Нехай маємо множину диз'юнктів:

1. B(x,a);

2. B(c,a)C(f(x));

3. C(y)D(a,f(x));

4. D(a,f(x))B(x,a)C(y).

Тоді ербранівський універсум:

Du={a,c,f(a),f(c),f(f(a)),f(f(c)),... },

а ербранівський базис прийме вид:

A={B(a,a),B(c,a),... ,C(a),C(c),C(f(a)),... ,D(a,f(a)),D(a,f(f(a))),... }.

По черзі перебираючи елементи ербранівського базису, будуємо дерево:

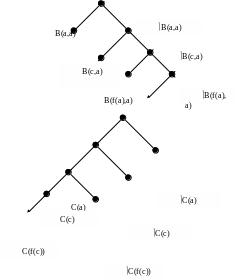
Нескінченність дерева випливає з нескінченності ербрановського базису. Проте за допомогою наведених нижче правил ми можемо впорядкувати перебір елементів ербранівського базису і встановити суперечливість множини диз'юнктів на фрагменті повного семантичного дерева.

1. Формуємо множину основних прикладів диз'юнктів.

2. Вибираємо диз'юнкт, що містить мінімальну кількість літер.

3. Будуємо фрагмент повного семантичного дерева, що містить у якості міток ребер літери, що входять у цей диз'юнкт.

4. Один із вузлів отриманого дерева - спростовуючий. Виключаємо з розгляду розгалуження з диз'юнкта, що спростовує.

5. Вибираємо один із листів , що залишилися , і перевіряємо за допомогою часткової інтерпретації значення істиності диз'юнктів, що залишилися.

6. Вибираємо той диз'юнкт, для спростування якого необхідно знати значення істиності мінімальної кількості літер.

7. З цього вузла продовжуємо будувати дерево, перехід на крок 4.

Приклад 1. Множина диз’юнктів розглянута вище.

1.	S = { B(c,a),	(1)
	B(c,a)C(f(c)),	(2)
	C(f(c))D(a,f(a)),	(3)
	D(a,f(a))B(c,a)C(f(c)). }	(4)

2. Вибираємо перший диз'юнкт B(c,a).

3. Будуємо дерево:

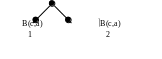
4. Вузол 1 - спростовуючий, і тому виключаємо з розгляду розгалуження з цього вузла.

5. Для встановлення значення істиності другого диз'юнкта треба знати значення істинності однієї літери, а для третього та четвертого - двох літер.

6. Вибираємо другий диз'юнкт.

7. Продовжуємо побудову дерева з обраного вузла:

Далі використовуючи алгоритм, одержуємо:

Реалізація Гілмора. Нехай множина диз'юнктів має вигляд:

S={ (a) (a) (a)	(1)
(a) (a)	(2)
(a) (a)	(3)
(a) }	(4)

Введемо позначення (a) - А, (a) - B, (a) - C. Тоді одержимо S={(BAС)(BC)(AC)C}. Зведемо множину S до ДНФ, користуючись співвідношенням (ab)c=(ac)(bc) і викреслюючи елементарні кон'юнкції з контрарними парами: S=((BB)(AB)(CB)(BC)(AC)C)((A C)(CC)=

=(ABAC)(CBAC)(BCAC)(CAC) = . Отримали порожню множину, тому множина диз'юнктів суперечлива.

Метод Девіса і Патнема.

Нехай множина S має вигляд:

{ ABC	(1)
BCE	(2)
AB	(3)
CDECB	(4)
DC	(5)
ECA	(6)
DEC	(7)
BC	(8)
AC }	(9)

. Правило тавтологічних диз'юнктів.

Викреслюємо четвертий диз'юнкт тому що він містить контрарну пару, тобто є абсолютно істиним. Множина диз'юнктів прийме вигляд:

{ ABC	(1)
BCE	(2)
AB	(3)
DC	(5)
ECA	(6)
DEC	(7)
BC	(8)
AC. }	(9)

. Правило однолітерних диз'юнктів не можна застосувати, тому що множина основних прикладів диз'юнктів S не містить однолітерних диз'юнктів.

. Правило чистих літер.

Множина диз'юнктів містить чисту літеру Е.

Отже викреслюємо 2,6,7-й диз'юнкти. Множина диз'юнктів прийме вигляд:

{ ABC	(1)
AB	(3)
DC	(5)
BC	(8)
AC. }	(9)

V. Правило розщеплення.

Множина основних прикладів диз'юнктів має вигляд:

S'={ (ABC)(AB)(BC)(BC)(CA) };

Побудуємо множини S1 і S2:

S1={ (AC)A(CA) };

S2={ CC(CA) };

Множина S1S2 - суперечлива тоді і тільки тоді, коли обидві множини S1 і S2 - суперечливі.

Покажемо суперечливість множини S1.

5. Правило однолітерних диз'юнктів.

Викреслюємо диз’юнкт А и його заперечення й одержуємо С С. Ще одне застосування цього правила дає порожній диз’юнкт.

Покажемо суперечливість S2.

VI. Правило однолітерних диз'юнктів.

Викреслюємо диз'юнкт С и його заперечення й одержуємо порожній диз'юнкт.

Таким чином, множина головних прикладів диз'юнктів суперечлива. Отже, згідно з 2-им варіантом теореми Ербрана суперечлива і вихідна множина диз'юнктів.

Метод резолюцій Робінсона

S={ (a)  (x,y), (1)

(x)  (x,f(c))  (x,f(a)), (2)

 (a)  (x,y), (3)

 (x,y)}. (4)

Резольвенти, що отримані перебором за методом насичення з множини S, утворять множину S1:

S1={1,3 (x,y), (5)

1,4 (a), (6)

2,3 (x,f(c))  (f(a)), (7)

2,4 (x)  (f(a)), (8)

3,4 (x). } (9)

Резольвенти,що отримані за методом насичення з множин S і S1 до одержання порожнього диз’юнкта, утворять множину S2:

S2={1,9 (x,y),

2,9 (x,f(c))  (f(a)),

3,6 (x,y),

3,8 (x,y)  (f(a)),

4,5. }

Семантична резолюція.

Семантична резолюція припускає для скорочення перебору використовувати порядок літер (причому вибір порядку зазвичай залишається за користувачем, даються тільки загальні рекомендації) і розбиття множини диз'юнктів на підмножини (розбиття передбачається виконувати на основі інтепретації, вибір інтепретації залишається за користувачем, але також даються загальні рекомендації).

Зазвичай для побудови розбиття використовується гіперрезолюція, негативна або позитивна. З точки зору вибору порядку можна використовувати різноманітні поняття, зокрема дуже ефективним підходом є приписування старшинства літерам, що зустрічаються в одномісних диз'юнктах.

Розглянемо приклад:

S={ A(x,a)B(b,y), (1)

B(x,y)C(z), (2)

C(c), (3)

A(x,y)B(b,a)}. (4)

Розбиття: S'={(3)};

S''={(1),(2),(4)}.

Порядок: C>B>A.

Резольвенти:

(2),(3)B(x,y), уніфікатор  = {c/z} (поміщається в S' (5));

(1),(5)A(b,a), уніфікаторі  = {b/x} (поміщається в S' (6));

(5),(4)A(b,a), уніфікаторі  = {b/x,a/y} (поміщається в S'' (7));

(6),(7).

Показано, що семантична резолюція є повною, тобто якщо множина S суперечлива, то незалежно від вибору порядку і розбиття він буде виведений.

Але існують такі випадки, у яких одночасне застосування порядку і розбиття зробить дуже складним вивід порожнього диз'юнкта.

Розглянемо приклад:

Використовуючи будь-який інший метод, легко вивести порожній диз'юнкт. Спробуйте зробити це за допомогою методу семантичної резолюції.

ЛОК-резолюція.

У ЛОК-резолюції кожній літері множини диз'юнктів приписується індекс. Після чого застосовується метод резолюцій за правилом насичення, причому дозволяється відрізати тільки літери, що мають найменший індекс (кожна у своєму диз'юнкті).

Розглянемо приклад:

S={A₁²(x)A₁¹(x) A₁³(x), (1)

A₁²(x)A₁³(x), (2)

A₁¹(x)A₁³(x), (3)

A₁³(x)}. (4)

Введемо індексацію:

S={₁A₁²(x)₂A₁¹(x)₃A₁³(x), (1)

₄A₁²(x)₅A₁³(x), (2)

₆A₁¹(x)₇A₁³(x), (3)

₈A₁³(x)}. (4)

ЛОК-резольвенти:

(1),(2)₂A₁¹(x)₃A₁³(x) ₅A₁³(x), склейка ₂A₁¹(x)₃A₁³(x); (5)

(1),(3) - не можна виконувати ЛОК-резолюцію, тому що найменший індекс у диз'юнкті (1) має літера ₁A₁²(x).

(5),(3) ₇A₁³(x) ₃A₁³(x), склейка ₃A₁³(x); (6)

(6),(4).

Лінійна резолюція.

Головна ідея лінійної резолюції полягає в побудові дерев виводу специфічного вигляду. Ці дерева повинні містити мінімальну кількість ребер, тому що ефективність методу тим вище, чим менша кількість ребер у побудованому дереві. Для досягнення цієї мети в лінійній резолюції використовується метод пошуку в глибину.

S={A₁¹(x), (1)

A₁¹(x)A₂¹(a,f(x))A₂²(x,c), (2)

A₂²(x,c) A₂¹(y,f(x)), (3)

A₂²(x,c) } (4)

Впорядкована лінійна резолюція.

Відмінність впорядкованої резолюції від лінійної полягає у використанні концепції впорядкованого диз'юнкта. Ми переходимо від розгляду диз'юнкта як множини літер до розгляду диз'юнкта як послідовності літер. Крім того, відрізаємі літери не губляться. Інформація про них зберігається у виляді так званих обрамлених літер.

S={ A²₁(x,b), (1)

A²₂(f(a),y), (2)

A¹₁(x)A¹₂(a), (3)

A¹₁(x)A¹₂(a), (4)

A²₁(c,b) A²₂(f(a),y) A¹₁(c) A¹₂(a), (5)

A²₁(c,b) A²₂(f(a),y) A¹₂(a) A¹₁(c). } (6)

Метод резолюцій для клауз Хорна.

Спочатку необхідно представити вихідну множину S диз'юнктів у вигляді клауз Хорна. Для цього скористаємося означенням клаузи Хорна. Клауза - це секвенція, у якій використовуються тільки атомарні формули справа і зліва. Отже, необхідно представити множину S у вигляді множини секвенцій. Секвенція - це вираз виду А₁, А₂, А₃,... А_m B₁, B₂, B₃,... B_n. B нашому випадку секвенції А₁, А₂, А₃,... А_m; B₁, B₂, B₃,... B_n будуть тільки літерами. Клаузи звичайно записуються в оберненому порядку, тобто клауза буде мати вигляд B₁, B₂, B₃,... B_n  А₁, А₂, А₃,... А_m . Слід врахувати, що в явному виді заперечення в клаузальній формі логіки немає. Неявно його заміняють переносом атомарної формули в іншу частину клаузи. Також клаузи Хорна допускають наявність у лівій частині не більш однієї атомарної формули. Для зведення секвенції до такого вигляду іноді потрібна заміна предикатів.

Приклад.

Нехай S={ AB, (1)

CA, (2)

AB, (3)

C } (4) - вихідна множина диз'юнктів.

Запишемо множину S у вигляді секвенцій:

A,B (1)

C,A (2)

A,B (3)

C (4)

Приведемо секвенції до виду клауз:

1. A,B (1)

2. A,C ; A,C (2)

3. A,B ; AB (3)

4.C (4)

Перша клауза містить у лівій частині дві атомарні формули.

Введемо заміну A=D. Тоді:

1. D,B ; BD (1)

2. D,C ; BC (2)

3. DB ; B,D (3)

4.C (4)

Множина клауз Хорна, що описує дану множину диз'юнктів, має вигляд:

BD (1)

DC (2)

B,D (3)

C (4)

Резольвенти:

(1),(2) : BC (5)

(3),(2) : B,C (6)

(5),(4) : B (7)

(6),(7) : C (8)

(8),(4) : 

Наявність порожньої клаузи говорить про присутність протиріччя, отже дана множина диз'юнктів суперечлива.

Застосування методів автоматичного доказу теорем до теорій з нелогічними аксіомами.

Нехай необхідно встановити істиність наступної теореми G=t(t=t). Тобто необхідно перевіряти істиність теореми наступного вигляду:

(A6A7)G або (A6A7G), де

(A6) x(x=x) ;

(A7) xy((x=y)(A(x,x)A(x,y))).

Перейдемо від встановлення істиності до встановлення суперечливості заперечення і приведемо до ССФ.

A6A7Gx(x=x)xy((x=y)(A(x,x)A(x,y)))t(t=t)

xy((x=x)((x=y)(A(x,x)A(x,y))))t(t=t)

txy((x=x)((x=y)A(x,x)A(x,y))(t=t))

xy((x=x)((x=y)A(x,x)A(x,y))(a=a)).

Отже множина диз'юнктів має наступний вигляд:

S={ (x=x), (1)

(x=y)A(x,x)A(x,y), (2)

(a=a). } (3)

Скориставшись правилом резолюцій Робінсона легко одержуємо вивід порожнього диз'юнкта.

(1),(3),  = {a/x}.

Отже, логічно зробити висновок про те, що теорема G=t(t=t) – істинна в теорії.

СПИСОК ЛІТЕРАТУРИ