
- •Теорія ймовірностей`
- •1. Скінченний та зліченний імовірносний простір. Геометричне визначення імовірності
- •1.2. Події та операції над подіями
- •1.3. Скінченний простір елементарних подій
- •1.4. Зліченна ймовірносна схема
- •1.5. Геометричне визначення ймовірності
- •2. Аксіоматика теорії ймовірностей
- •2.1. Поняття ймовірносного простору. Властивості ймовірності
- •2.2. Умовні ймовірності. Незалежність подій
- •2.3. Формула повної ймовірності і формула Байєса
- •3. Дискретні випадкові величини
- •3.1. Поняття дискретної випадкової величини
- •3.2. Закон розподілу дискретної випадкової величини
- •3.3. Математичне сподівання
- •3.4. Багатовимірні закони розподілу
- •3.5. Додаткові властивості математичного сподівання і дисперсії
- •3.6. Коваріація та коефіцієнт кореляції
- •3.7. Нерівність Чебишова і закон великих чисел
- •3.8. Генератриси цілочислових випадкових величин
- •3.9. Багатовимірні генератриси
- •3.10. Гіллясті процеси
- •3.11. Слабка збіжність випадкових величин
- •3.12. Граничні теореми в схемі Бернуллі
- •4. Випадкові величини загального типу
- •4.1. Визначення випадкової величини. Її функція розподілу
- •4.2. Розподіл ймовірностей випадкової величини. Вибірковий ймовірносний простір
- •4.3. Дискретні, абсолютно неперервні і сингулярні розподіли
- •4.4. Функції від випадкових величин
- •4.5. Багатовимірні розподіли
- •4.6. Незалежність випадкових величин
- •4.7. Математичне сподівання
- •4.8. Теорема Лебега. Формули для обчислення математичного сподівання
- •4.9. Закон великих чисел і метод Монте-Карло
- •4.11. Характеристична функція. Її основні властивості
- •4.12. Формули обернення для характеристичних функцій
- •4.13. Неперервна відповідність між функціями розподілу і характеристичними функціями
- •4.14. Закон великих чисел у формі Хінчина
- •4.15. Центральна гранична теорема
3.11. Слабка збіжність випадкових величин
Будемо говорити, що
послідовність
![]() (послідовність законів розподілів)
збігається слабко до розподілу
(послідовність законів розподілів)
збігається слабко до розподілу
![]() ,
якщо для будь-якого k
,
якщо для будь-якого k
![]() .
.
Відзначимо, що догранична послідовність чисел задовольняє умовам
![]() і
і
![]() .
.
Таким же умовам задовольняє і гранична послідовність.
Будемо
говорити, що послідовність випадкових
величин
![]() слабко збігається
до випадкової величини
і писати
слабко збігається
до випадкової величини
і писати
![]() ,
якщо слабко збігаються відповідні їм
закони розподілу.
,
якщо слабко збігаються відповідні їм
закони розподілу.
Теорема
3.11. Нехай
![]() – послідовність ймовірносних генератрис,
а
– послідовність ймовірносних генератрис,
а
![]() – генератриса послідовності
.
Для того, щоб при кожному k
необхідно і достатньо, щоб при усіх
– генератриса послідовності
.
Для того, щоб при кожному k
необхідно і достатньо, щоб при усіх
![]()
![]() .
.
3.12. Граничні теореми в схемі Бернуллі
Нехай – число успіхів у n незалежних випробуваннях Бернуллі з ймовірністю успіху p у кожному випробовуванні. Таким чином
![]()
![]() .
.
Будемо вважати, що від n залежить не тільки число успіхів, але й p=pn – ймовірність успіху.
Теорема 3.12 (теорема
Пуассона). Якщо при
![]()
![]() ,
то для довільного фіксованого
,
то для довільного фіксованого
![]()
![]() .
.
Теорема 3.13 (локальна
теорема Муавра-Лапласа).
Нехай в схемі n
випробувань Бернуллі ймовірність
успіху
![]() - стала величина. Тоді при
і m
таких, що
- стала величина. Тоді при
і m
таких, що
 (
(![]() – довільна стала)
– довільна стала)
![]() ,
,
де
![]() - деяка стала величина.
- деяка стала величина.
Теорема 3.14 (інтегральна теорема Муавра-Лапласа). Якщо ймовірність успіху у кожному випробуванні - стала, то при
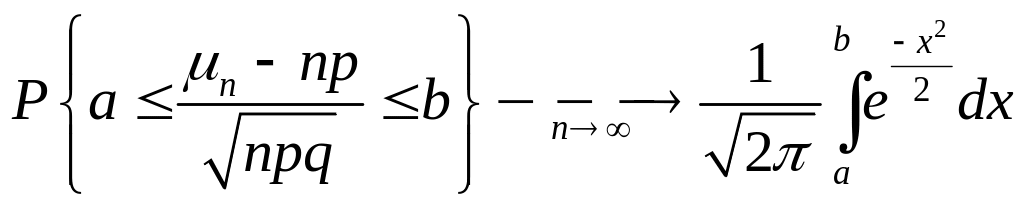
при
довільних
![]() .
.
4. Випадкові величини загального типу
4.1. Визначення випадкової величини. Її функція розподілу
Нехай
– довільний ймовірносний простір.
Числову функцію
![]() від елементарної події
від елементарної події
![]() будемо називати випадковою величиною,
якщо для довільного числа x
будемо називати випадковою величиною,
якщо для довільного числа x
![]() .
.
Функцію
![]() ,
визначену при усіх
,
визначену при усіх
![]() ,
будемо називати функцією розподілу
випадкової величини
.
,
будемо називати функцією розподілу
випадкової величини
.
Лема
4.1. Функція розподілу
![]() випадкової величини
задовольняє властивостям:
випадкової величини
задовольняє властивостям:
а) для
![]()
![]() ;
;
b)
![]() .
.
Наслідок 4.1. Якщо функція розподілу випадкової величини , то
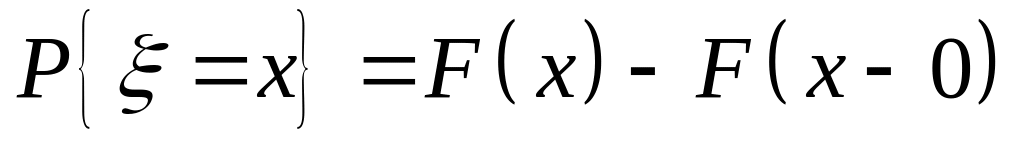 ;
;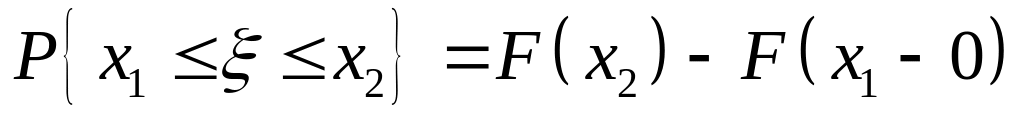 ;
; ;
;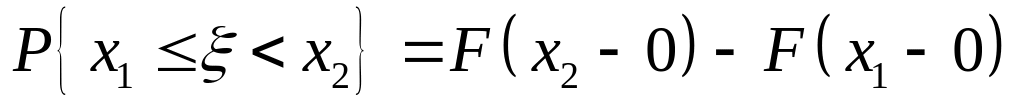 .
.
Характеристичні властивості функції розподілу містить наступна теорема.
Теорема 4.1. Функція розподілу має слідуючі властивості:
1) F(x) – неспадна;
2) F(x) – неперервна справа;
F(+ ∞)=1;
F(- ∞)=0.
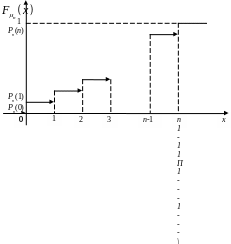
Розглянемо приклад функції
розподілу.
Нехай
– число успіхів в схемі
випробувань Бернуллі з ймовірністю
успіху
![]() .
Тоді
.
Тоді
![]() ,
,
![]() .
.
Функцію розподілу можна подати у вигляді
![]() .
.
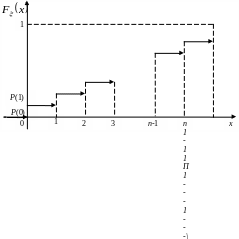
Тепер нехай
– випадкова величина, яка має розподіл
Пуассона з параметром
![]() ,
,
![]() ,
,
![]() .
.
Тоді
![]() представляє собою функцію розподілу
.
представляє собою функцію розподілу
.
4.2. Розподіл ймовірностей випадкової величини. Вибірковий ймовірносний простір
Далі через BR
будемо позначати
-алгебру
борелівських множин R,
тобто мінімальну
![]() -алгебру,
яка містить множини виду
-алгебру,
яка містить множини виду
![]() ,
для будь-якого
.
,
для будь-якого
.
Лема 4.2. Нехай A0 – деякий клас підмножин R,
{A0}
– мінімальна
-
алгебра, яка містить A0,
а
![]() – дійсна функція, яка визначена на
просторі елементарних подій
.
Якщо для будь-якого
– дійсна функція, яка визначена на
просторі елементарних подій
.
Якщо для будь-якого
![]() A0
A0
![]() ,
то для будь-якого
,
то для будь-якого
![]() {A0}
{A0}
![]() .
.
Наслідок
4.2.
Якщо
– випадкова величина,
то для кожної множини
![]() BR,
BR,
![]() і визначена ймовірність
і визначена ймовірність
![]() .
.
Для доведення достатньо замість A0 узяти клас множин виду , для будь-якого .
Тепер
можна дати ”симетричне” визначення
випадкової величини. Випадкова величина
– це довільне вимірне відображення
вимірного простору
![]() у вимірний простір (R,
BR).
у вимірний простір (R,
BR).
Функція
![]() ,
визначена для усіх
BR,
називається розподілом ймовірностей
випадкової величини .
,
визначена для усіх
BR,
називається розподілом ймовірностей
випадкової величини .
