Розділ 5. Многочлени.

§ 1. Комплексні числа.

1. Довідка. У шкільному курсі математики знайомство з числами відбувається в такій послідовності: 1) множина натуральних чисел , 2) множина цілих чисел , 3) множина раціональних чисел , 4) множина дійсних чисел , причому

,

тобто кожна попередня множина є підмножиною наступної. Необхідність таких розширень викликана наступним.

Сума двох натуральних чисел завжди є числом натуральним, тобто дія додавання в множині не виводить за межі цієї множини. Обернену дію – віднімання – не завжди можна здійснити в множині . Для того, щоб дія віднімання стала можливою, доводиться множину доповнити від’ємними числами, розширивши тим самим до . Іншими словами, в множині цілих чисел рівняння , , завжди має розв’язок, тоді як в множині – не завжди.

Дія множення не виводить за межі множини , однак обернену дію – ділення – не завжди можна виконати в цій множині. Щоб це стало можливим, доводиться доповнити множину дробовими числами до множини раціональних чисел , що рівносильне тому, що рівняння , , , не завжди має розв’язки в множині , але завжди має розв’язки в множині .

Розширення множини раціональних чисел до множини дійсних чисел викликане потребою забезпечити існування розв’язків алгебраїчних рівнянь. Наприклад, квадратне рівняння з раціональними коефіцієнтами не має розв’язків у множині раціональних чисел , але має два розв’язки в множині дійсних чисел . Таким чином, розширення множини раціональних чисел до множини дійсних чисел забезпечує існування розв’язків квадратних рівнянь з раціональними коефіцієнтами, які мають додатний дискримінант. Потреби математики вимагають розширення множини дійсних чисел так, щоб і рівняння з від’ємним дискримінантом мало розв’язки у новій розширеній множині чисел. З такої точки зору нас і буде цікавити рівняння

. (1)

2. як розширення . Нагадаємо, що число називається раціональним, якщо його можна подати у вигляді звичайного дробу

, , .

Оскільки множина раціональних чисел як розширення множини буде слугувати зразком для побудови комплексних чисел, то нагадаємо основні властивості раціональних чисел.

Для раціональних чисел визначено дії додавання та множення за формулами

(2)

Таке означення дій з раціональними числами продиктоване необхідністю включити у (2) додавання і множення цілих чисел як окремого випадку раціональних чисел.

Додавання та множення в множині раціональних чисел мають такі властивості:

1) асоціативність:

,

,

2) комутативність:

,

,

3) дистрибутивність:

.

Далі, з формул (2) негайно випливає, що раціональні числа можна віднімати та ділити, не виходячи за межі множини .

Зазначимо, що точно такі самі властивості має і множина дійсних чисел .

Насамкінець зауважимо, що запис раціонального числа у вигляді звичайного дробу склався історично і є відбитком його походження. В раціональному числі істотним є те, що воно є впорядкованою парою цілих чисел, де на першому місці записано чисельник, а на другому – знаменник. При переході до такого запису дії додавання та множення набувають такого доволі “дивного” вигляду

.

3. Означення комплексних чисел. Множиною комплексних чисел будемо називати множину впорядкованих пар дійсних чисел , , для якої визначено операції додавання та множення за формулами

(3)

. (4)

Два числа і називаються рівними, якщо , .

Легко показати, що визначені за таким правилом операції є асоціативними, комутативними і зв’язані дистрибутивністю. Доведемо, наприклад, дистрибутивність.

.

З рівності правих частин обох рівностей випливає рівність лівих частин, так що

і дистрибутивність доведено.

Вправа. Довести, що операції додавання та множення є комутативними та асоціативними.

Покажемо тепер, що в множині комплексних чисел можна виконувати обернені операції.

Різницею комплексних чисел і має бути комплексне число , для якого

.

За (3)

,

тобто

.

Остаточно

. (5)

З (5) дістаємо, що нулем у множині комплексних чисел є пара .

З’ясуємо можливість ділення. Нехай і – два комплексних числа, причому , тобто . Часткою від ділення числа на має бути комплексне число , для якого

.

Звідси, на підставі (4),

.

Розв’язавши систему, дістанемо

, .

Отже, частка існує і однозначно визначена рівністю

. (6)

Звідси, зокрема, одиницею є пара .

Покажемо, що множина комплексних чисел є розширенням множини дійсних чисел, тобто, що . Для цього зауважимо, що між множиною комплексних чисел, які мають вигляд і множиною дійсних чисел існує взаємно однозначна відповідність , а формули (3) і (4) для таких пар дають

,

тобто пари, які мають вигляд додаються і множаться між собою так само, як відповідні дійсні числа, тому пару можна ототожнити з дійсним числом , .

Залишилося показати, що серед комплексних чисел є розв’язок рівняння (1). Таким розв’язком є пара :

.

Пару позначають літерою , так що .

Насамкінець зауважимо, що визначення операцій додавання та множення за формулами (3), (4) є єдино можливим для забезпечення тих вимог, які було поставлено до розширення .

4. Алгебраїчна форма комплексного числа. Для комплексних чисел застосовується більш зручний запис. Зауважимо, що

.

Звідси,

.

Така форма комплексного числа називається алгебраїчною. називається уявною одиницею, – дійсною частиною, – уявною частиною.

Відповідно до рівностей (3), (4), (5), (6) операції над комплексними числами в алгебраїчній формі записуються так

(3′)

(5′)

(4′)

(6′)

тобто при додаванні (відніманні) комплексних чисел окремо додаються (віднімаються) дійсні частини і окремо уявні, а при множенні вони перемножуються як двочлени з врахуванням того, що . Дія ділення зводиться до домножування чисельника і знаменника на число, яке відрізняється від знаменника лише знаком уявної частини.

Якщо , то число називається спряженим до і позначається , так що .

Вправа. Перевірити, що справджуються такі рівності:

,

,

.

Крім того,

,

тобто сума і добуток спряжених комплексних чисел є числа дійсні.

5. Геометричне зображення комплексних чисел. Домовимось комплексне число зображувати точкою площини, абсциса якої у вибраній прямокутній декартовій системі координат дорівнює , а ордината – . Тим самим між множиною всіх комплексних чисел і точками площини встановлено взаємно однозначну відповідність. При цьому дійсним числам відповідають точки осі абсцис, яку називають дійсною віссю. Суто уявним числам відповідають точки осі ординат, яку називають уявною віссю, а саму площину – комплексною площиною. З другого боку, кожній точці комплексної площини взаємно однозначно можна співставити її радіус-вектор . Таким чином, будь-яке комплексне число можна трактувати або як точку комплексної площини, або як радіус-вектор точки .

6. Тригонометрична форма комплексного числа. З комплексними числами в алгебраїчній формі зручно виконувати операції додавання, віднімання і множення. Складніше виконувати операцію піднесення до степеня, і зовсім не видно, як добувати корінь з комплексного числа. Використовуючи геометричну інтерпретацію комплексних чисел знайдемо іншу форму комплексного числа, яка дасть змогу розв’язати як задачу піднесення до степеня, так і задачу добування кореня будь-якого натурального степеня з комплексного числа.

З рисунка, , .

Звідси,

. (7)

Отриманий запис називається тригонометричною формою комплексного числа. називається модулем числа і позначається , а кут – аргументом цього числа і позначається .

Очевидно,

, (8)

а кут визначається з рівностей

, . (9)

Зазначимо, що кут з рівностей (9) визначається з точністю до доданків, кратних , оскільки є періодом та . Тому поряд із зображенням (7) справджується і така рівність

. (10)

У більшості випадків, подаючи комплексне число в тригонометричній формі, аргумент беруть у межах .

7.Множення і ділення комплексних чисел. Додавати і віднімати комплексні числа в тригонометричній формі незручно, але множити і ділити зручно. Нехай

.

Знайдемо добуток .

.

Звідси,

(11)

(12)

тобто модуль добутку дорівнює добутку модулів, а аргумент добутку – сумі аргументів співмножників.

Аналогічні правила справджуються для частки:

.

Звідси,

(13)

. (14)

8. Піднесення до цілого степеня. Формула Муавра. Розглянемо операцію піднесення комплексного числа до цілого степеня.

Теорема. Для будь-якого цілого справджується рівність

. (15)

Доведення. Методом математичної індукції доведемо спочатку, що формула (15) справджується для натуральних . При формула очевидна. Припустимо, що формула справджується для всіх показників аж до . Тоді

,

тобто формула справджується і для . За принципом математичної індукції вона справджується для всіх , .

Нехай тепер ціле від’ємне число. Покладемо , . Тоді

.

Рівність (15) називається формулою Муавра.

9. Добування кореня з комплексного числа. Коренем -го степеня з комплексного числа називається таке комплексне число , що і позначається символом , .

Якщо , то . Нехай тепер , , тобто . Припустимо, що існує і дорівнює . Тоді

.

За формулою Мавра

.

Оскільки два комплексних числа рівні тоді і лише тоді, коли їх модулі рівні, а аргументи відрізняються доданком, кратним , то

, ,

Звідси,

, .

Остаточно

. (16)

Покажемо, що корінь -го степеня має рівно різних значень. Справді, при отримується різних значень, оскільки збільшення на одиницю призводить до збільшення аргументу на .

Нехай тепер не збігається з жодним із значень . Тоді , тому , і

,

тобто значення аргументу при даному відрізняється від значення аргументу при на доданок, кратний . Це означає, що при даному отримується таке саме значення кореня, як і при , тобто таке, що входить в множину .

Отже, добування кореня з комплексного числа завжди можливе і дає різних значень. Очевидно, що всі значення кореня розміщені на колі радіуса з центром у початку координат і ділять це коло на рівних частин.

10. Корені з одиниці. Значення називають коренями – го степеня з одиниці і позначають символами . Їх можна знайти за формулою (16), поклавши в ній , , так що

, .

Звідси, зокрема, .

Теорема 1. Всі значення кореня – го степеня з комплексного числа можна отримати множенням одного з цих значень на кожен з коренів – го степеня з одиниці.

Доведення. Нехай – який-небудь корінь – го степеня з , тобто , а – будь-який корінь з 1, тобто . Тоді , тобто також є коренем – го степеня з .

Розглянемо добутки . Кожен з цих добутків, за щойно доведеним, є коренем – го степеня з . Нехай , , . Тоді , бо у супротивному з рівності випливає рівність , що неможливо. Отже, всі ці добутки є різними значеннями кореня – го степеня з .

Теорема 2. Добуток довільних двох коренів – го степеня з 1 є коренем – го степеня з 1.

Доведення. Нехай і – корені – го степеня з 1, тобто , . Тоді , тобто є коренем – го степеня з 1.

Теорема 3. Число, обернене до кореня – го степеня з одиниці, є коренем -го степеня з одиниці.

Доведення. Справді, для довільного кореня – го степеня з одиниці маємо . З очевидної рівності випливає, що , або . Звідси, , що й означає, що є коренем – го степеня з одиниці.

За формулою Муавра легко знайти :

.

Підсумовуючи, зазначимо, що множина коренів –го степеня з одиниці має такі властивості: 1) операція множення елементів цієї множини не виводить за межі множини (теорема 2), до того ж асоціативність множення коренів – го степеня з одиниці випливає з асоціативності множення комплексних чисел; 2) в множині існує елемент з такою властивістю: ; 3) для будь-якого елемента в множині існує обернений елемент , . Виконання таких трьох умов означає, що множина коренів – го степеня з одиниці утворює групу відносно операції множення комплексних чисел.

Вправа. Довести, що будь-який цілий степінь кореня – го степеня з одиниці також є коренем – го степеня з одиниці.

11. Первісні корені. Нехай є коренем -того степеня з одиниці, тобто , і нехай . Тоді є коренем – го степеня з одиниці: . Іншими словами, серед коренів – го степеня з одиниці можуть бути корені з одиниці нижчого степеня. Проте для кожного натурального серед коренів – го степеня з одиниці є такі, що не є коренями з одиниці жодного з нижчих степенів. Наприклад, для кореня – го степеня з одиниці при всіх натуральних отримуємо

,

тобто не є коренем з одиниці жодного з нижчих степенів.

Означення. Корінь – го степеня з одиниці називається первісним, якщо він не є коренем з одиниці жодного меншого степеня.

Теорема. Корінь – го степеня з одиниці є первісним тоді і лише тоді, коли число взаємно просте з числом .

Доведення. Позначимо через найбільший спільний дільник чисел і .

Нехай і не є взаємно простими, тобто і нехай , . Тоді і

,

тобто , , тому не є первісним коренем – го степеня з одиниці.

Нехай тепер , тобто і взаємно прості. Припустимо, що є коренем степеня з одиниці, . Тоді

, .

Звідси, – ціле число, тобто ділиться на . Це означає, що кожний простий множник, на які розкладається число , зустрічається в розкладі на прості множники або числа , або числа . Оскільки , то прості множники числа не можуть вичерпати всіх простих множників числа . Звідси, існує принаймні один простий множник числа , який є одночасно і множником числа , тому числа і не є взаємно простими. Це, однак, суперечить умові, що .

Наслідок. Число первісних коренів – го степеня з одиниці дорівнює кількості цілих додатних чисел, менших від і взаємно простих з ним.

12. Поняття про кільце. Непорожня множина , на якій визначено операції додавання та множення, називається кільцем, якщо виконуються такі умови:

1. множина є абельовою групою за додаванням;

2. операція множення асоціативна;

3. операції додавання і множення зв’язані властивістю дистрибутивності.

Якщо операція множення комутативна, то кільце називається комутативним. Якщо множина елементів кільця скінченна, то кільце називається скінченним, у супротивному випадку – нескінченним. Якщо в кільце входить одиничний елемент, то кільце називається кільцем з одиницею, у супротивному – кільцем без одиниці. Кільце, елементами якого є числа, називається числовим кільцем.

Приклади числових кілець.

1. Множина цілих чисел є комутативним кільцем з одиницею. Справді, множина є абельовою групою за додаванням, а операція множення цілих чисел асоціативна, комутативна і дистрибутивна відносно операції додавання.

2. Множина цілих парних чисел є комутативним кільцем без одиниці.

3. Множини  , , раціональних, дійсних і комплексних чисел відповідно є комутативними кільцями.

4. Множина, що складається з одного числа 0, є кільцем, яке називається нульовим і позначається .

Приклади нечислових кілець.

1. Кільце квадратних матриць. Позначимо через множину всіх квадратних матриць – го порядку, елементами яких є дійсні числа. Відповідні властивості операції додавання матриць [Розділ 1, §1, п.5] показують, що множина є абельовою групою відносно додавання матриць. Операція множення матриць асоціативна і пов’язана законом дистрибутивності з операцією додавання [розділ 1, §1, п.7]. Отже, множина через є кільцем, яке називається кільцем квадратних матриць – го порядку над . Оскільки операція множення матриць некомутативна, то кільце некомутативне.

Аналогічними міркуваннями легко переконатися, що множини , , квадратних матриць – го порядку з елементами із , , відповідно також утворюють кільця.

2. Кільце класів лишків. Нехай – довільне натуральне число, а кільце цілих чисел.

Цілі числа називаються конгруентними за модулем , якщо при діленні кожного з них на отримується одна й та сама остача, або, що все-одно, якщо різниця ділиться на без остачі. Число називається модулем конгруенції. Запис

читається « конгруентне за модулем ». Наприклад, ( або ), ( або ).

Позначимо через множину всіх цілих чисел, при діленні кожного з яких на дістаємо остачу , тобто , і будемо називати її класом цілих чисел, конгруентних за модулем , або стисло, класом лишків за модулем . Наголосимо, що . Очевидно, що кільце цілих чисел розбивається на класів ,

,

які попарно не перетинаються.

На множині класів лишків за модулем визначимо операції додавання і множення. Покажемо спочатку, що всі суми будь-яких чисел з класу і всеможливих чисел з класу належать одному й тому самому класові. Справді, , . Тоді

Звідси, операцію додавання в множині класів лишків за модулем природно визначити так:

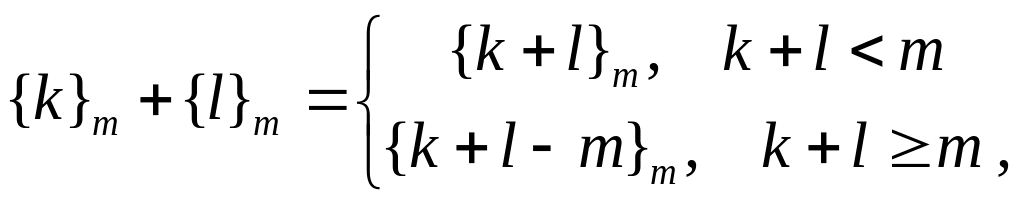
тобто сумою класів і називається клас, до якого належить сума будь-якого числа з і будь-якого числа з , зокрема і сума .

Добутки будь-яких чисел з і будь-яких чисел з також належать одному й тому самому класові , де – остача від ділення на :

.

Таким чином, операцію множення класів лишків за модулем логічно визначити так:

.

Так визначені операції додавання й множення класів лишків асоціативні, комутативні і пов’язані законом дистрибутивності. Це випливає з того, що асоціативність, комутативність та дистрибутивність справджуються для операцій додавання та множення в кільці цілих чисел і того зв’язку між операціями над цілими числами і над класами лишків.

Клас , який складається з чисел, що діляться на без остачі, відіграє в множині класів лишків роль нульового елемента. Оскільки , то клас є протилежним до класу . З викладеного дістаємо, що множина класів лишків є абельовою групою за додаванням. На цій групі визначено операцію множення, до того ж ця операція асоціативна, комутативна та пов’язана законом дистрибутивності з операцією додавання. Таким чином, множина класів лишків є комутативним кільцем, яке називається кільцем класів лишків за модулем і позначається . Часто класи лишків позначаються символами відповідно.

Для прикладу, кільце класів лишків за модулем 4 складається з чотирьох елементів: .Операції додавання і множення цих класів здійснюється згідно з таблицями додавання й множення:

13. Поняття про поле. Комутативне кільце називається полем, якщо для нього справджуються такі умови:

1. В кільце входить щонайменше два елементи;

2. – кільце з одиницею;

3. Кожний ненульовий елемент має обернений елемент.

Поле називається скінченним, якщо множина його елементів скінченна і нескінченним у супротивному випадку.

Приклади.

1. Кільця є полями.

2. Множина дійсних чисел, які мають вигляд , , є полем (довести як вправу).

3. Довести, що сукупність дійсних чисел , , не утворює поля, а множина дійсних чисел , , є полем.

Поле класів лишків за простим модулем.

Покажемо, що комутативне кільце класів лишків за модулем , де – деяке просте число, є полем.

В кільце входить , , елементів. Клас є одиницею кільця . Покажемо, що кожний ненульовий елемент має обернений елемент. Для цього розглянемо сукупність з натуральних чисел

(*)

і покажемо, що в кожному класі кільця міститься рівно одне число сукупності (*). Покажемо спочатку, що жодне з чисел сукупності (*) не входить в клас , тобто не ділиться на . Якби це було не так, то для , , , . Звідси . Розкладемо чисельник на прості множники, . Позаяк , то , , і тому не може скоротитися з жодним із множників , . З тої самої причини не може скоротитися з жодним із множників , , тому . Суперечність. Отже, жодне з чисел сукупності (*) не ділиться на , тому жодне з них не входить в клас . Крім того, жодна пара чисел , сукупності (*) не входить до одного класу, бо у супротивному випадку їх різниця повинна ділитись на , що неможливо за щойно доведеним. Звідси, в кожний з ненульових класів входить одне і лише одне число сукупності (*)

Нехай число , , входить у клас . Позаяк , , то за означенням добутку класів лишків, . Таким чином, елемент кільця є оберненим до елемента . Отже, кільце є полем.