§ 5. Сложение случайных и систематических погрешностей

В реальных опытах присутствуют как систематические, так и: случайные ошибки. Пусть они характеризуются стандартными: погрешностями σ_сист и σ_случ. Суммарная погрешность находится по формуле

(7)

Поясним эту формулу. Систематическая и случайная ошибки могут, в зависимости от случая, складываться или вычитаться друг из друга. Как уже говорилось, точность опытов принято характеризовать не максимальной (и не минимальной), а среднеквадратичной погрешностью. Поэтому правильно рассчитанная погрешность должна быть меньше суммы σ_сист+σ_случ и больше их разности |σ_сист–σ_случ|. Легко видеть, что σ_полн, определенная формулой (7), удовлетворяет этому условию. В самом деле, σ_полн, σ_сист и σ_случ – величины положительные. Поэтому

_.

Знак равенства возникает только в том случае, когда одна из погрешностей равна нулю. Аналогично имеем

.

Формула (7) показывает, что при наличии как случайной, так и систематической погрешности полная ошибка опыта больше, чем каждая из них в отдельности, что также является вполне естественным.

Обратим внимание на важную особенность формулы (7). Пусть одна из ошибок, например σ_случ, в 2 раза меньше другой – в нашем случае σ_сист - Тогда

.

К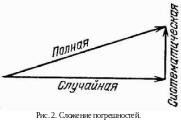 ак мы уже говорили, погрешности редко удается оценить с точностью лучше 20%. Но в нашем примере с точностью 20% σ_сист=σ_случ. Таким образом, меньшая погрешность почти ничего не добавляет к большей, даже если она составляет половину от нее. Этот вывод очень важен. В том случае, если случайная ошибка опытов хотя бы вдвое меньше систематической, нет смысла производить многократные измерения, так как полная погрешность опыта при этом практически не уменьшается. Измерения достаточно произвести 2–3 раза, чтобы убедиться, что случайная ошибка действительно мала.

Схему сложения погрешностей поясняет рис. 2. Полная погрешность равна гипотенузе треугольника, катеты которого равны σ_сист и σ_случ.

§ 6. Обработка результатов при косвенных измерениях

Если исследуемая величина равна сумме или разности двух измеренных величин,

А=В±С, (8)

то наилучшее значение величины А равно сумме (или разности) наилучших значений слагаемых: А_наил= В_наил± С_наил, или, как рекомендовано выше,

= ± . (9)

Здесь и в дальнейшем угловые скобки (или черта сверху) означают усреднение: вместо того, чтобы писать А_ср, будем пользоваться обозначением <А> (или ), и т. д.

Среднеквадратичная погрешность σ_А, если величины В и С независимы, находится по формуле

, (10)

т. е. погрешности, как всегда, складываются квадратично. (Иначе говоря, складываются не погрешности, а дисперсии результатов измерений.) При обсуждении формулы (10) следует использовать те же аргументы, которые были приведены в связи с формулой (7).

В том случае, если искомая величина равна произведению пли частному двух других,

А =B · С или А=В/С, (11)

то

= · или = / . (12)

Относительная среднеквадратичная погрешность произведения и частного независимых величин находится по формуле

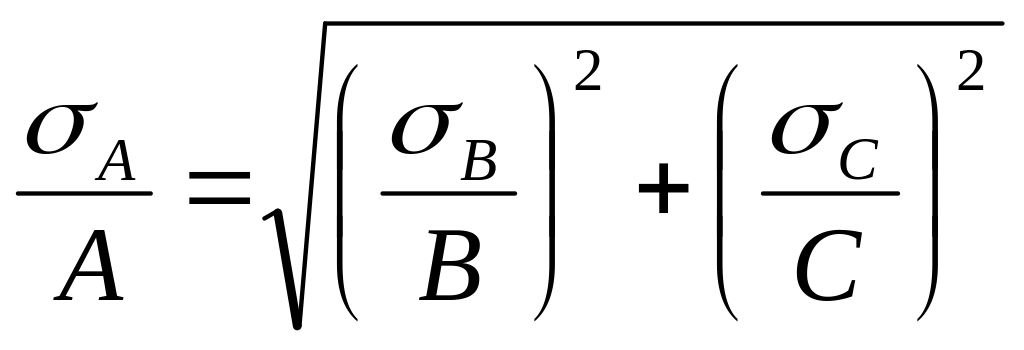. (13)

Приведем расчетные формулы для случая, когда

А =B^βС^γE^ε…, (14)

Наилучшее значение А связано с наилучшими значениями В, С, Е и т. д. той же формулой (14), что и каждое конкретное значение. Относительная среднеквадратичная погрешность величины А при независимых В, С, Е, ... находится по формуле

(15)

Наконец, приведем для справок общую расчетную формулу. Пусть

А =f(B, С, E,…), (16)

где f – произвольная функция величин В, С, Е и т. д. Тогда

А _наил =f(B_наил, С_наил, E_наил,…). (17)

Формула (17) справедлива как в том случае, когда B_наил, С_наил и т. д. непосредственно измерены, так и в том случае, если они сами найдены по измеренным значениям других величин. В первом случае значения B_наил, С_наил и т. д., как уже указывалось, равны , и т. д. Погрешность А находится но формуле

(18)

Обозначение ∂f/∂B имеет обычный смысл частной производной функции f по В, т. е. производной, при вычислении которой все остальные аргументы, кроме В (в нашем случае аргументы С, Е и т. д.), считаются постоянными. Аналогичный смысл имеют частные производные по С, Е и т. д. Частные производные следует вычислять при наилучших значениях аргументов B_наил, С_наил и т. д. Все приведенные в этом параграфе формулы являются частными случаями (17) и (18).

При нахождении частных производных тригонометрических функций следует иметь в виду, что табличные значения производных приведены для случаев, когда углы выражены в радианах. Поэтому во избежание ошибок углы, измеренные в градусах, и их погрешности рекомендуется переводить в радианы.¹

Рассмотрим некоторые следствия, которые могут быть получены из анализа формул, приведенных в этом разделе. Прежде всего заметим, что следует избегать измерений, при которых искомая величина находится как разность двух больших чисел. Так, толщину стенки трубы плохо определять, вычитая ее внутренний диаметр из внешнего (и, конечно, деля результат пополам). Относительная погрешность измерения, которая обычно представляет главный интерес, при этом сильно увеличивается, так как измеряемая величина – в нашем случае толщина стенки – мала, а ошибка в ее определении находится путем сложения погрешностей измерения обоих диаметров и поэтому возрастает. Следует также помнить, что погрешность измерения, которая составляет, например, 0,5% от величины внешнего диаметра, может составить 5 и более процентов от толщины стенки.

При измерениях, которые затем обрабатываются по формуле (11) (например, при определении плотности тела по его массе и объему), следует определять все измеряемые величины с приблизительно одинаковой относительной точностью. Так, если объем тела измерен с погрешностью 1 %, то при взвешивании с погрешностью 0,5% его плотность определяется с точностью 1,1%, а при взвешивании с погрешностью 0,01% – с точностью 1%, т. е. с той же, практически, точностью. Тратить силы и время на измерение массы тела с точностью 0,01% в этом случае, очевидно, не имеет смысла.

При измерениях, которые обрабатываются по формуле (14),. следует обращать главное внимание на точность измерения величины, входящей в расчетную формулу с наибольшим показателем степени.

Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно,. а на какие не нужно тратить больших усилий.