2.3. Уравнение неразрывности

Уравнение неразрывности, являющееся скалярным уравнением:

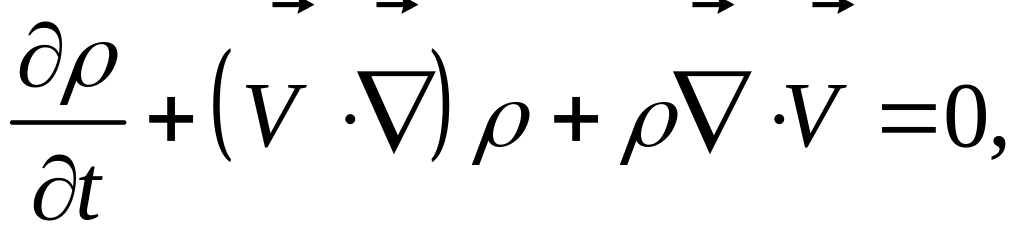
может быть записано еще в двух эквивалентной этой формах:

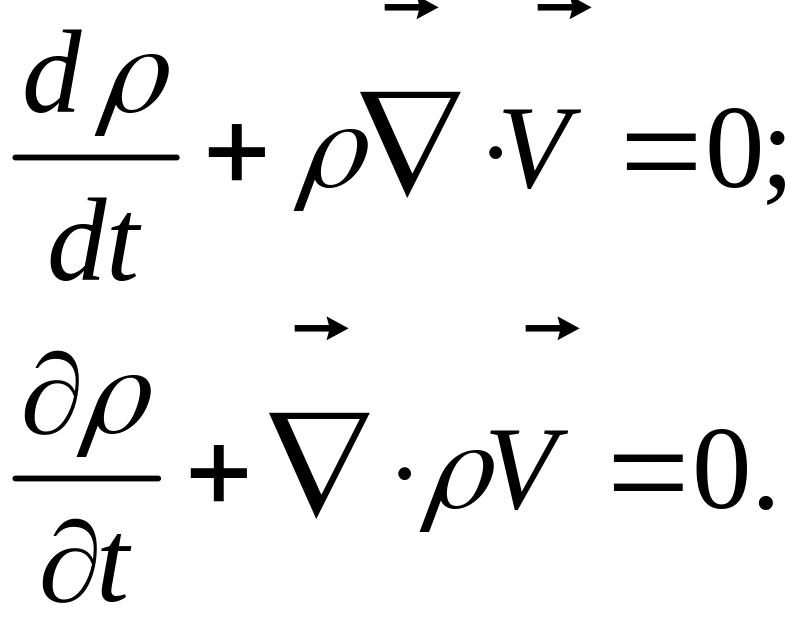
Для несжимаемой жидкости уравнение неразрывности примет вид:

В случае турбулентного движения это будет:

здесь трактуется уже как осредненная скорость, - пульсационная. Отсюда и для осредненной скорости, и для пульсационной имеем:

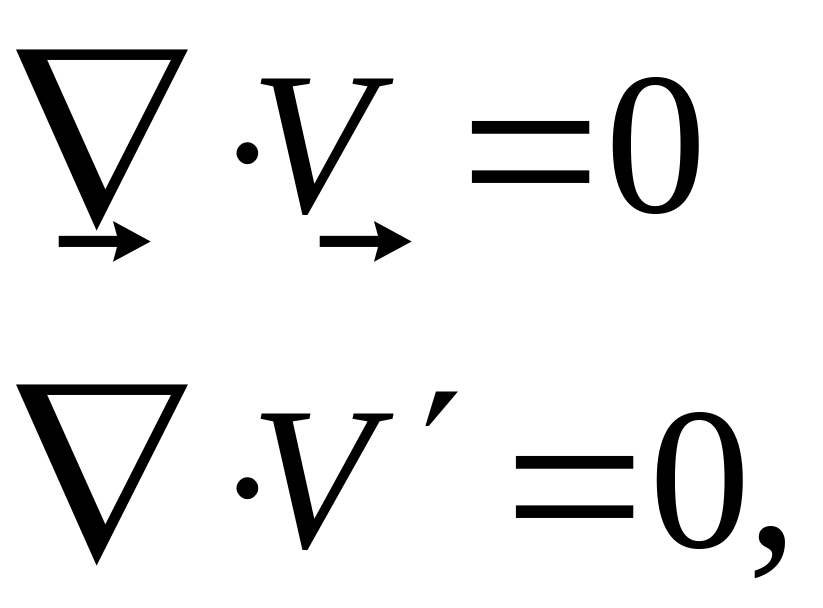
т.е. в компонентном виде:

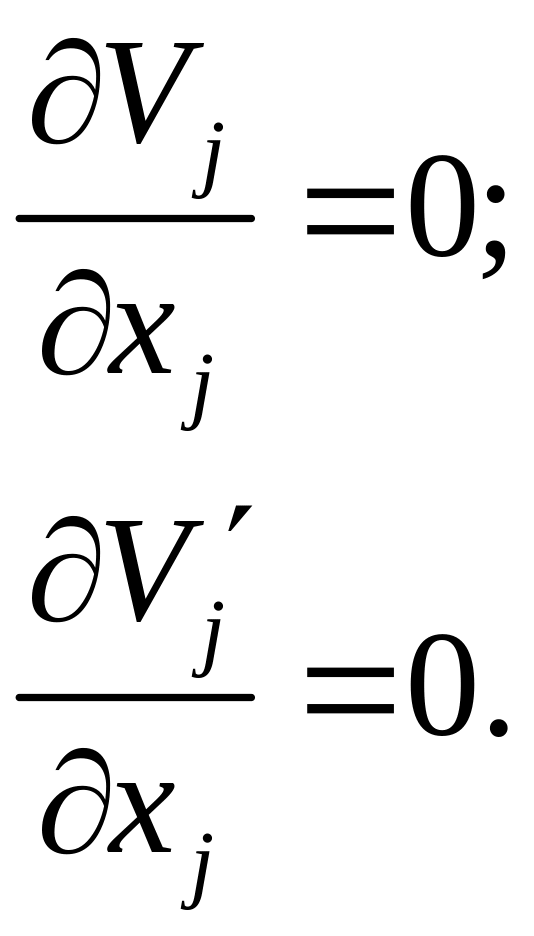
Рассмотрим дивергенцию тензора пульсаций третьего ранга, т.е. величину:

которая является тензором второго ранга. Простейшие преобразования дают:

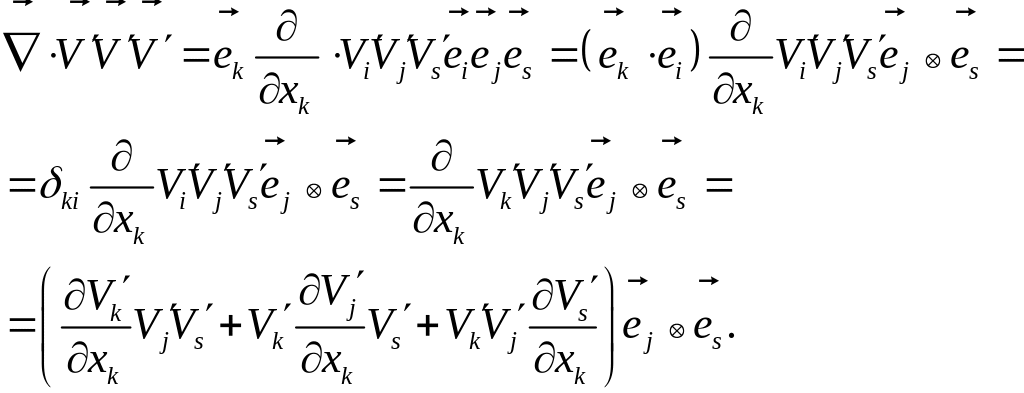
Первое слагаемое, согласно формуле, равно нулю, а два других дают:

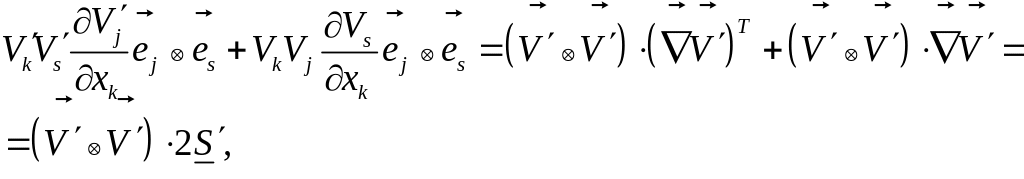
где - тензор пульсационных скоростей деформаций:

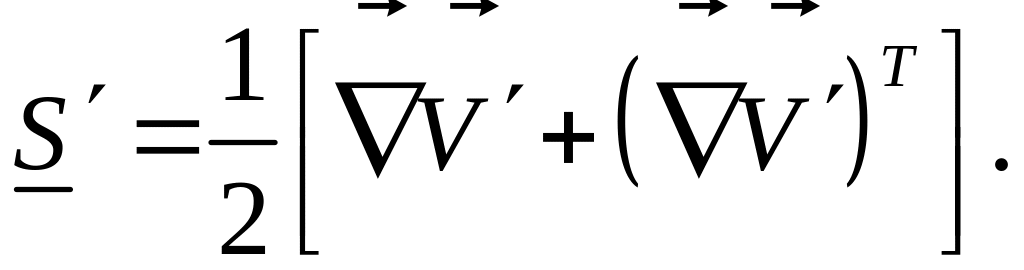
Выполняя операцию осреднение по Рейнольдсу, получаем для несжимаемой жидкости соотношение:

Применим к уравнению неразрывности, которое записано для общего случая движения жидкости любого вида, оператор градиента:

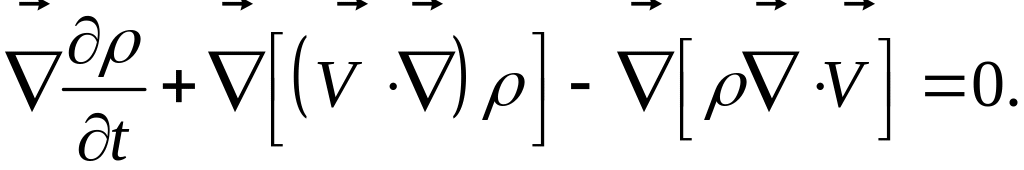
После несложных преобразований можно получить векторное уравнение:

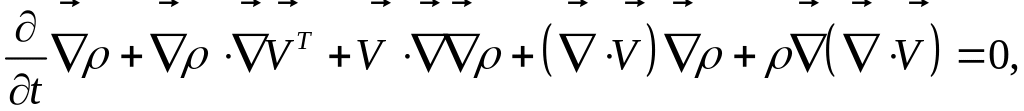
или, в более компактном виде:

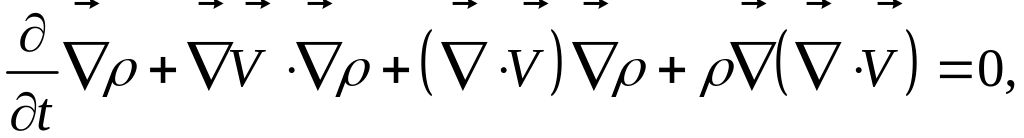
или, несколько иначе:

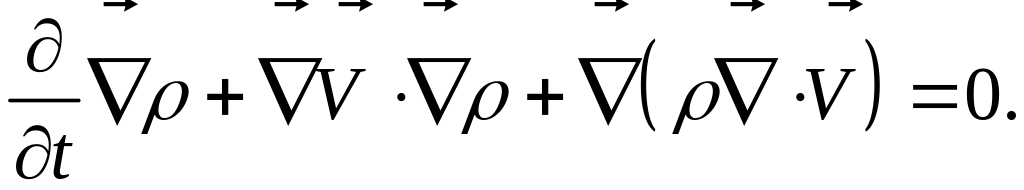(7)

Выражение (7) содержит градиент дивергенции вектора , который, как известно равен:

Для несжимаемой жидкости левая часть равна нулю, откуда для ротора ротора вектора скорости:

Для сжимаемой жидкости согласно формуле (7) в правой части этого соотношения появляются слагаемые:

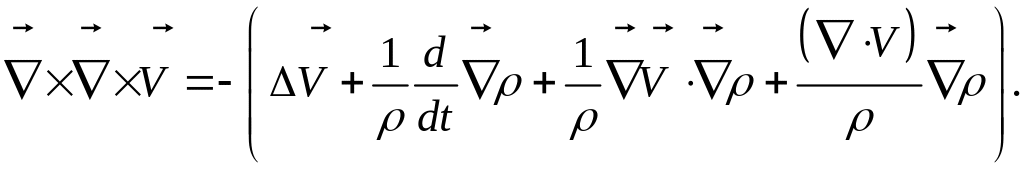
Тензорная форма уравнения неразрывности:

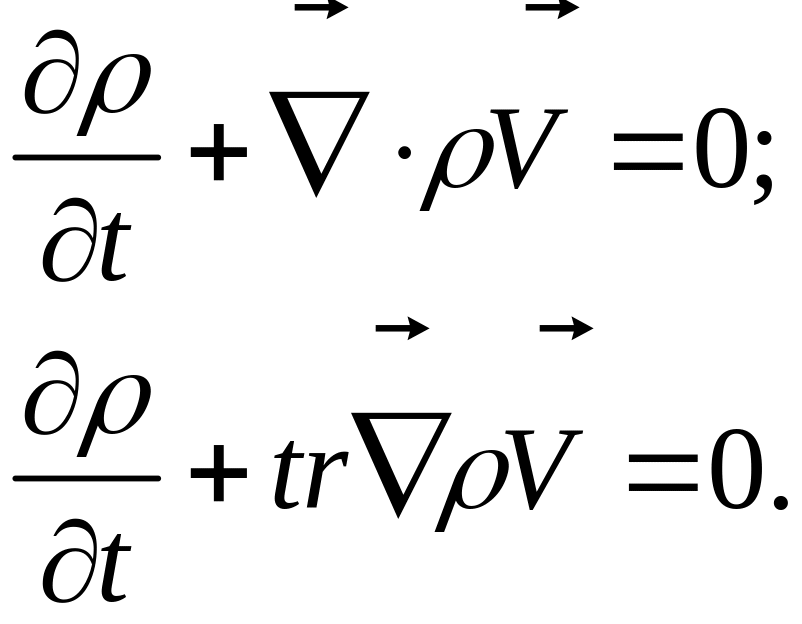(1)

Отсюда возникает тензор

Его можно представить:

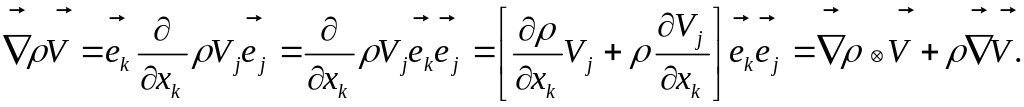
Отсюда возникают корреляции и

Поскольку уравнение неразрывности (1) можно т.е.

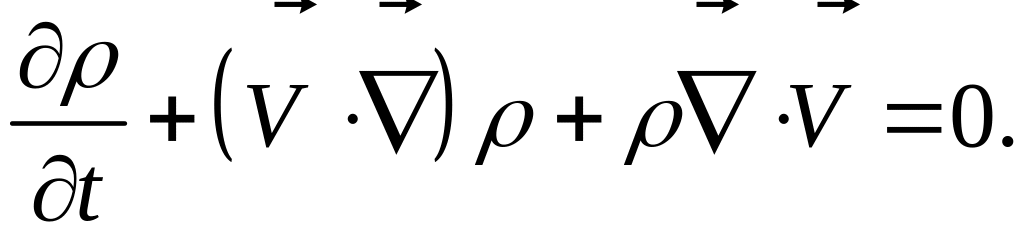
А можно записать для пульсационного движения:

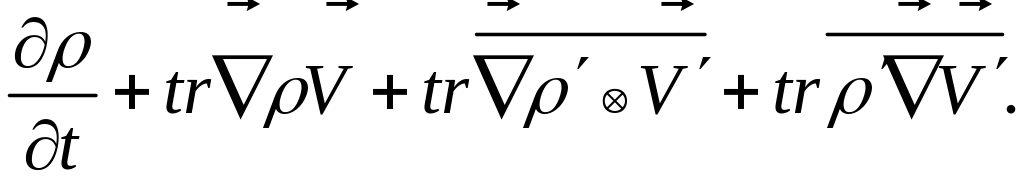
Любую конвективную производную скалярной величины можно записать в виде:

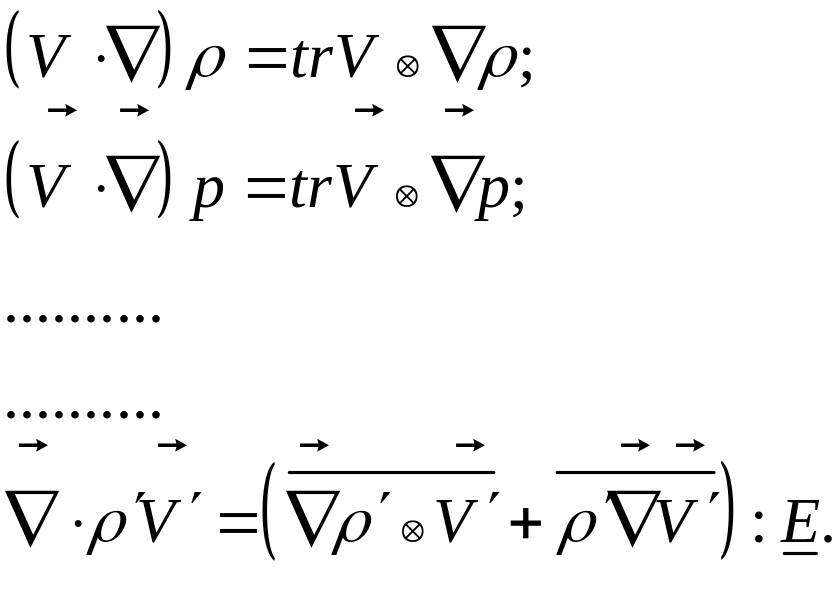
2.4 Уравнения движения жидкости с постоянными и переменными физическими свойствами.

Уравнение движения жидкости в напряжениях 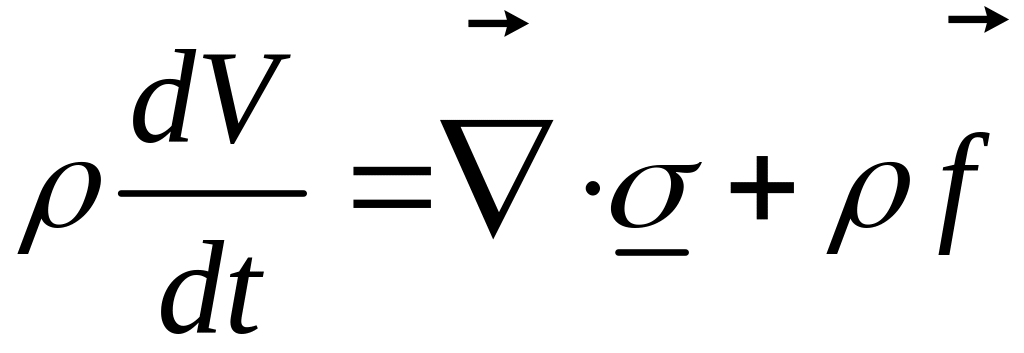содержит дивергенцию тензора напряжений Для несжимаемой жидкости тензор имеет вид:

Его дивергенция при учитывая что записывается как:

Тогда уравнение движения несжимаемой жидкости – уравнение Навье-Стокса при принимает вид:

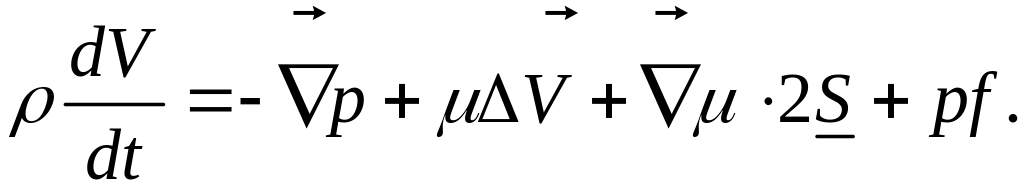
Добавочное слагаемое характеризует изменение динамической вязкости. В компонентной форме, в декартовой прямоугольной системе координат уравнение имеет вид:

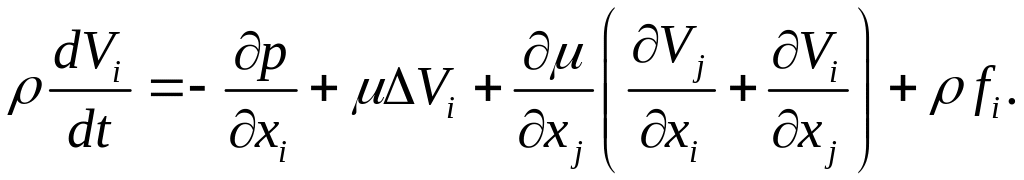
Для сжимаемой жидкости с переменной вязкостью уравнение будет содержать слагаемые с который в этом случае не будет равен нулю.

Реологическое соотношение при учете сжимаемости имеет вид:

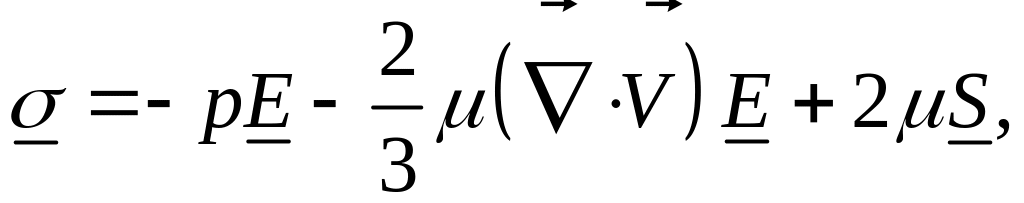
или, обозначая скалярную величину при единичном тензоре:

это соотношение можно записать в виде:

Дивергенция этого тензора:

и уравнение движения сжимаемой жидкости с переменной вязкостью принимает вид:

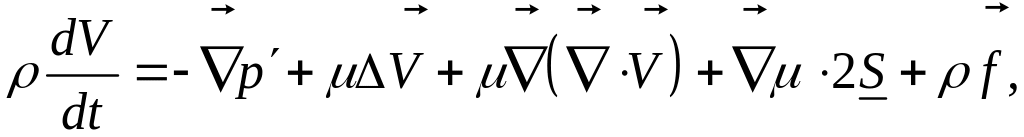
или, в компонентном виде:

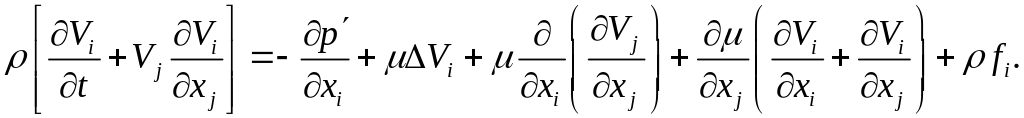
Учет переменности вязкости особенно важен при описании турбулентных течений с использованием модели Буссинеска с турбулентной вязкостью .

Применим операцию дивергенции к уравнению Навье-Стокса для сжимаемой жидкости с переменной вязкости, уравнение движения которой:

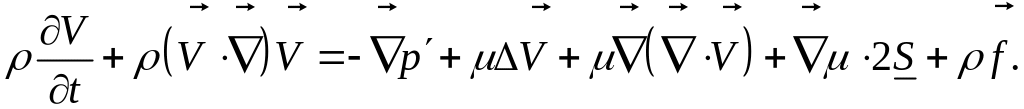
Будем последовательно применять операцию к каждому слагаемому этой формы:

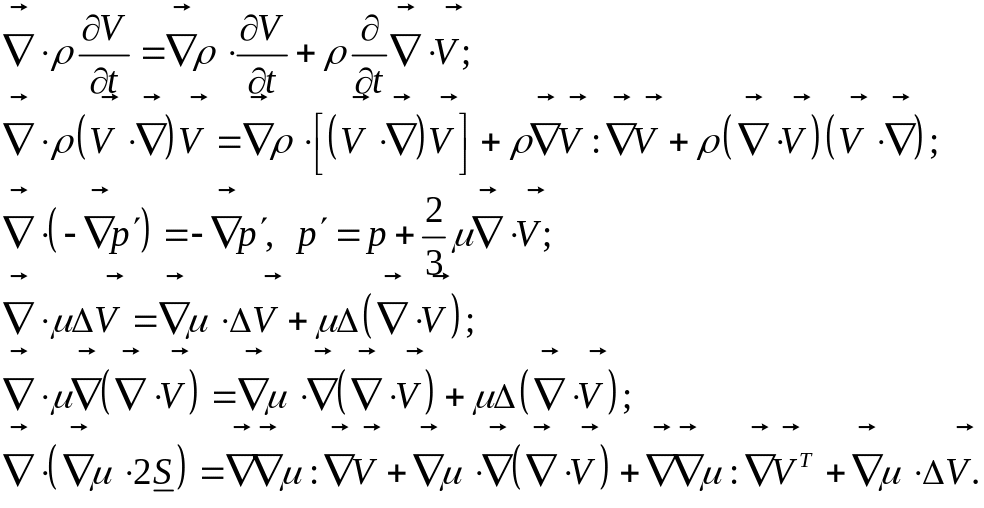
Если массовая сила характеризует поле сил тяжести, то она имеет потенциал

Тогда:

Поскольку потенциальная функция линейна, то её лапласиан равен нулю, в результате чего:

В итоге результат применения операции дивергенции дает скалярное уравнение:

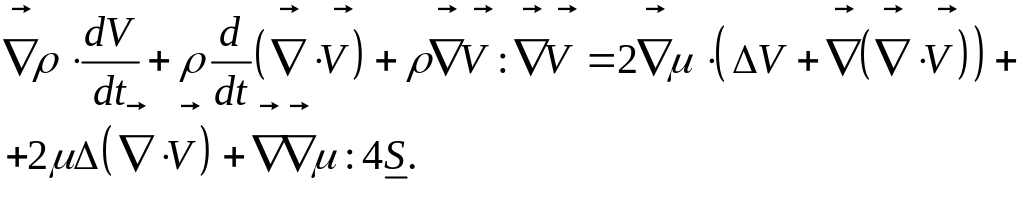
Если жидкость несжимаема, то это соотношение дает:

а если к тому же то

что и следовало ожидать.

Общий случай движения жидкости. Учет сжимаемой жидкости.

Для течений несжимаемой жидкости система уравнений состоит из уравнений Навье-Стокса и неразрывности (векторного и скалярного):

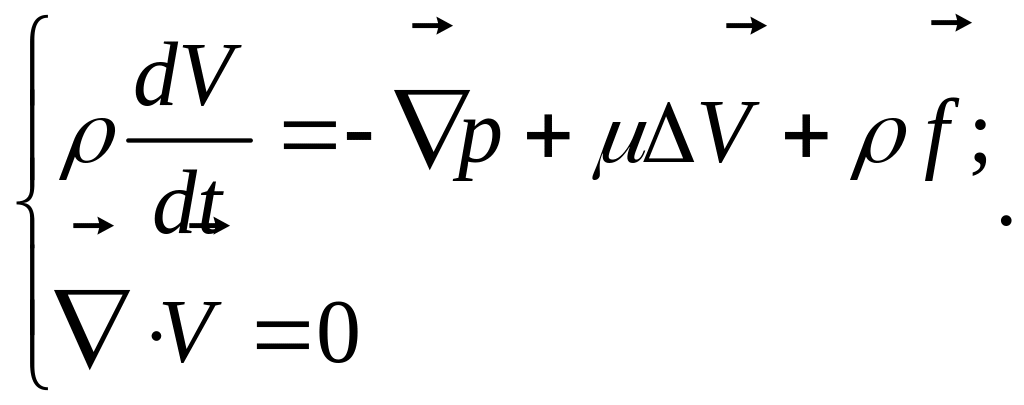(1)

Эта система из двух уравнений является замкнутой – содержит две неизвестных – вектор скорости и скалярную величину - давление. Система описывает ламинарные течения, в случае турбулентного она становится незамкнутой – появляется тензор рейнольдсовых напряжений, который требует своего определения.

Для течения сжимаемых сред и уравнение Навье-Стокса после подстановки реологического соотношения для стоксовой ньютоновской жидкости в уравнения движения сплошной среды в напряжениях принимает вид:

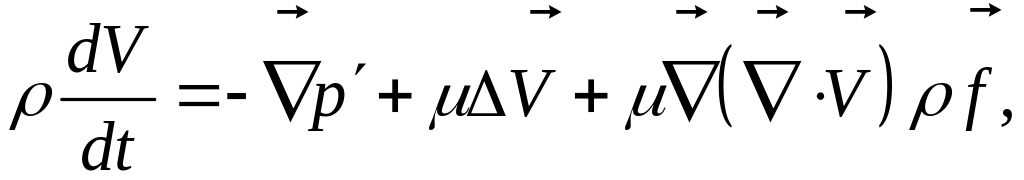(2)

где

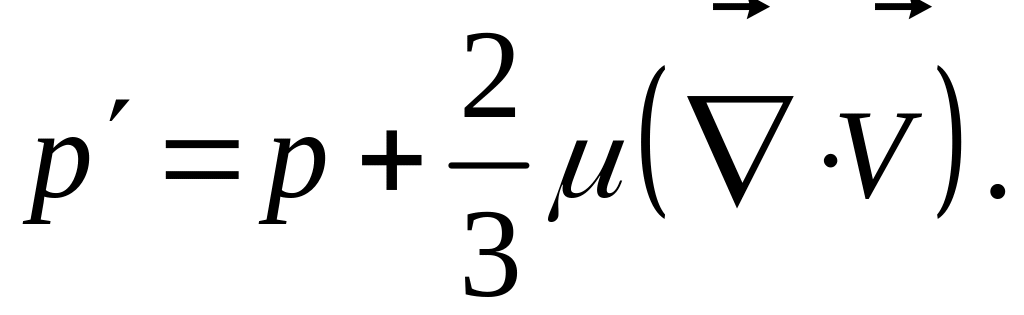(3)

Уравнения неразрывности для этого общего случая движения записывается как:

(4)

или, в несколько других эквивалентных формах:

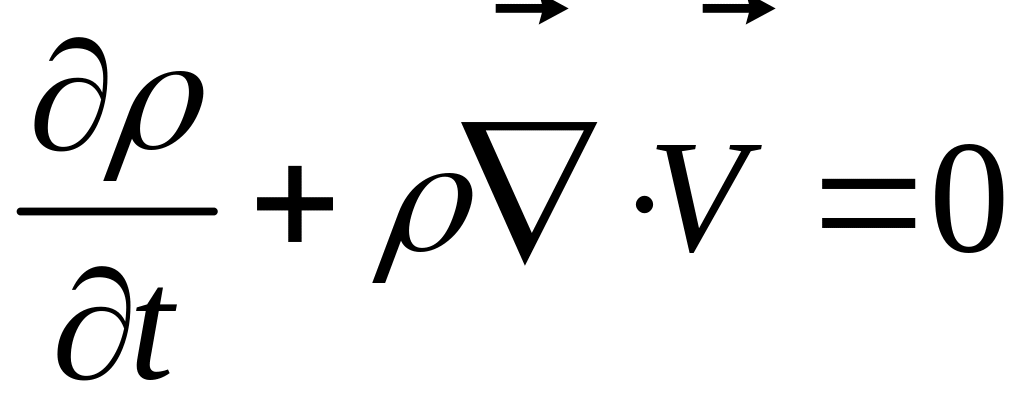
или

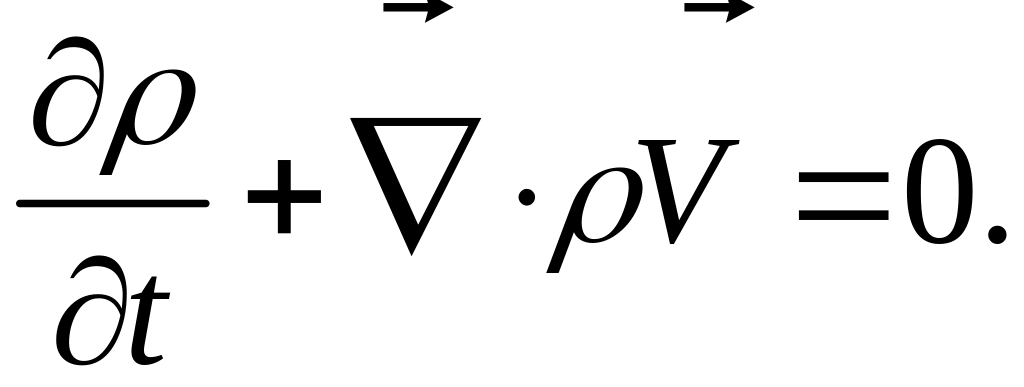
Видно, что при эти уравнения (2) и (4) приводят к системе (1).

При система уравнений (2) и (4) является незамкнутой – в ней дополнительно, по сравнению с системой уравнений (1) появляется еще одна неизвестная скалярная величина – плотность жидкости. Для замыкания системы используют уравнение энергии, в котором еще одну появляющуюся скалярную величину - выражают через термодинамическое уравнение состояния, к качестве которого обычно в газовой динамике выступает уравнение Менделеева-Клапейрона. Уравнение энергии можно записать в виде уравнения переноса для внутренней энергии :

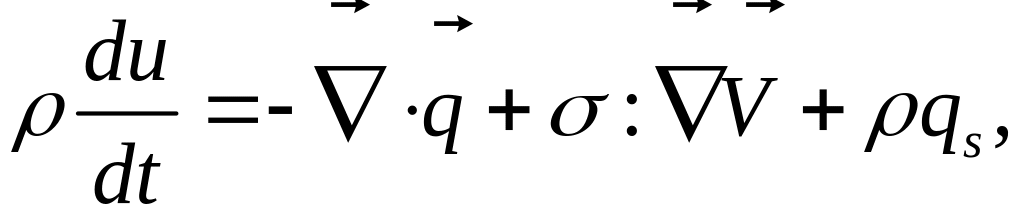(6)

где внутренняя энергия для идеального газа , она выражается через его изохорную теплоемкость, величина - интенсивность теплового потока, для ламинарного режима отвергает по закону теплопроводности Фурье где - коэффициент теплопроводности; - теплота, поступающая от внешних или внутренних источников.

Уравнения (2), (3), (4) справедливы для ламинарного режима движения. В случае турбулентного режима в них появляются корреляции, вызванные не только пульсациями скорости, но и пульсациями плотности и температуры.