2.10. Вихрь скорости и его ассоциированный тензор
Вихрь
является векторной величиной,
характеризующей поле скоростей:
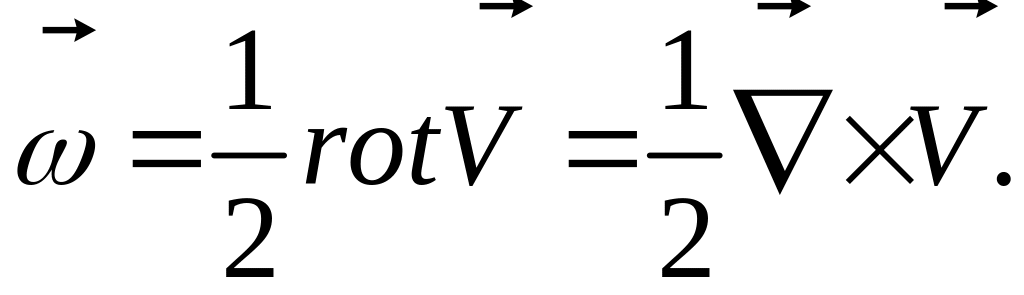(1)
В компонентном виде в декартовом базисе:
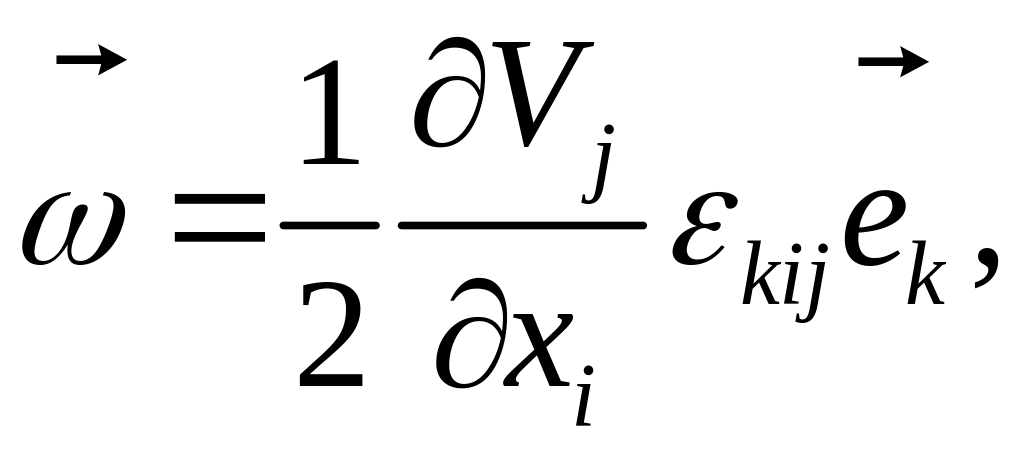
или, через определитель:
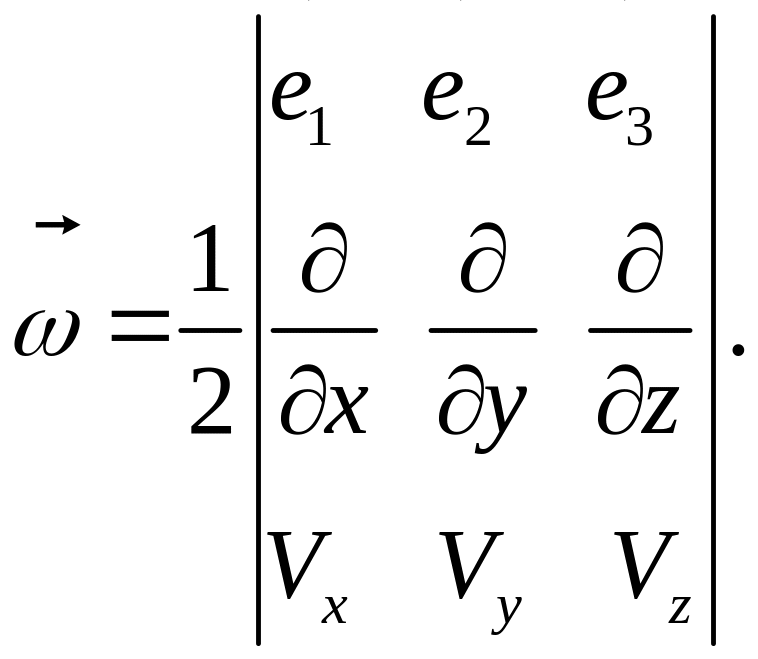
И в то, и в другом случае получаем для компонент вектора :
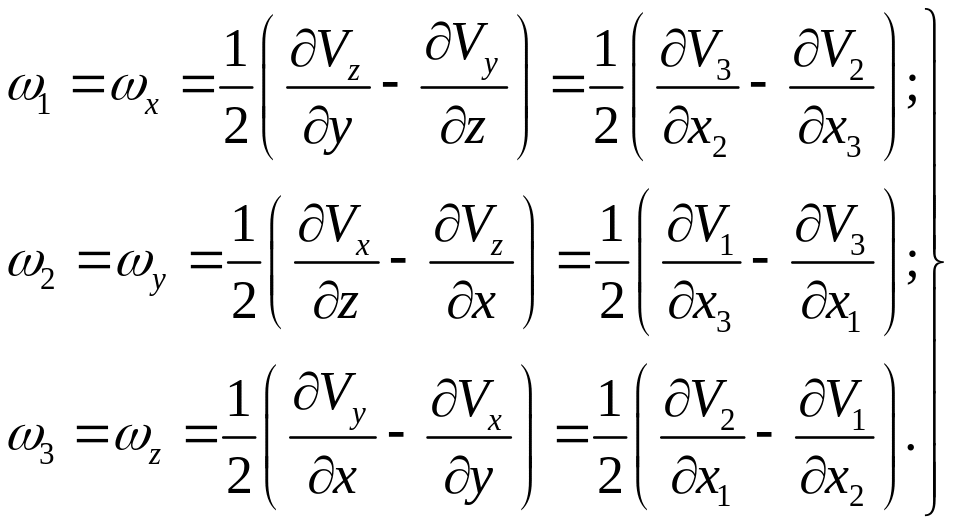(2)
Вектор угловой
скорости
и тензор вращения
связаны между собой через тензор
Леви-Чивита
.
Эти величины являются взаимно
ассоциированными. Говорят, что тензор
является ассоциированным по отношению
к вектору
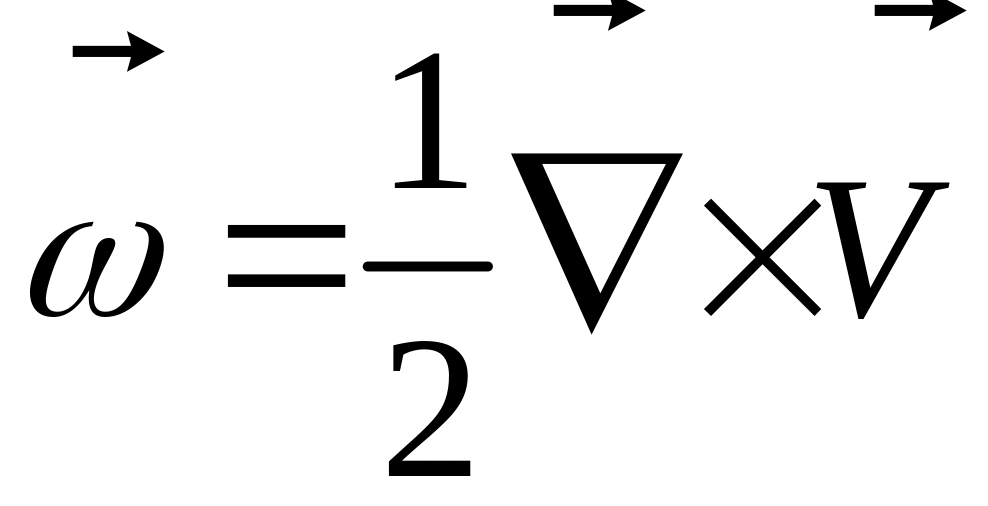поскольку выполняются соотношения:
(3)
И наоборот, вектор является ассоциированным по отношению к тензору поскольку справедливо:
(4)
В формуле (3) тензор переводится в вектор , а в формуле (4) вектору сопоставляется тензор вращения.
Докажем равенства (3) и (4).
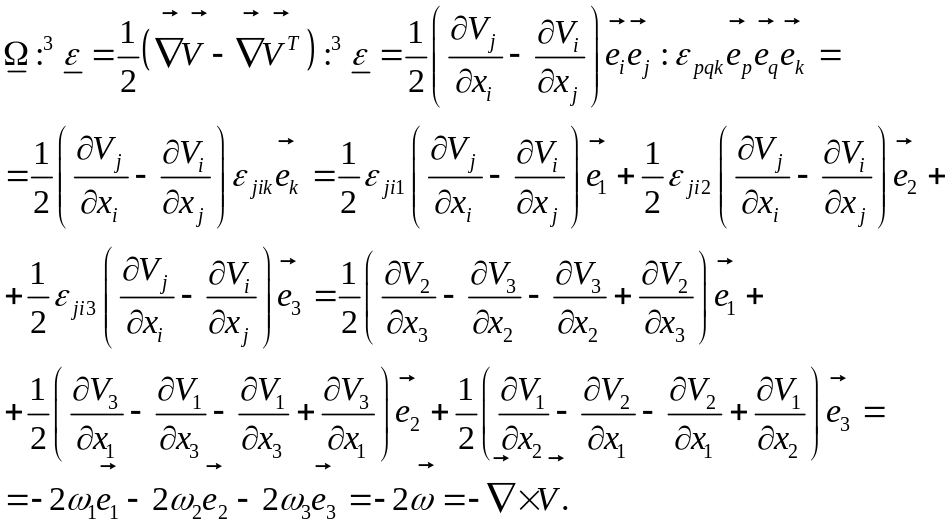
Тот же результат
получаем для
.
Для равенства (4) имеем:
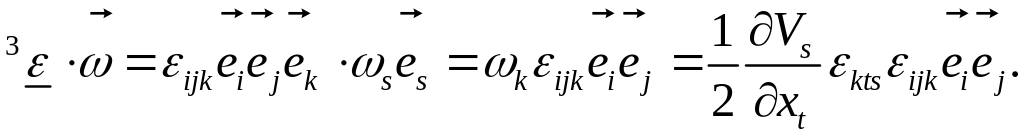
Компоненты этого тензора второго ранга имеют вид:
- при
они являются нулевыми;
- при
это:
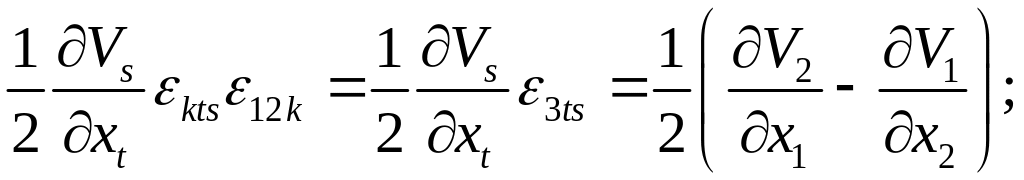
- аналогичным
образом можно получить значения для
всех
.
В итоге матрица компонент этого тензора
имеет вид:
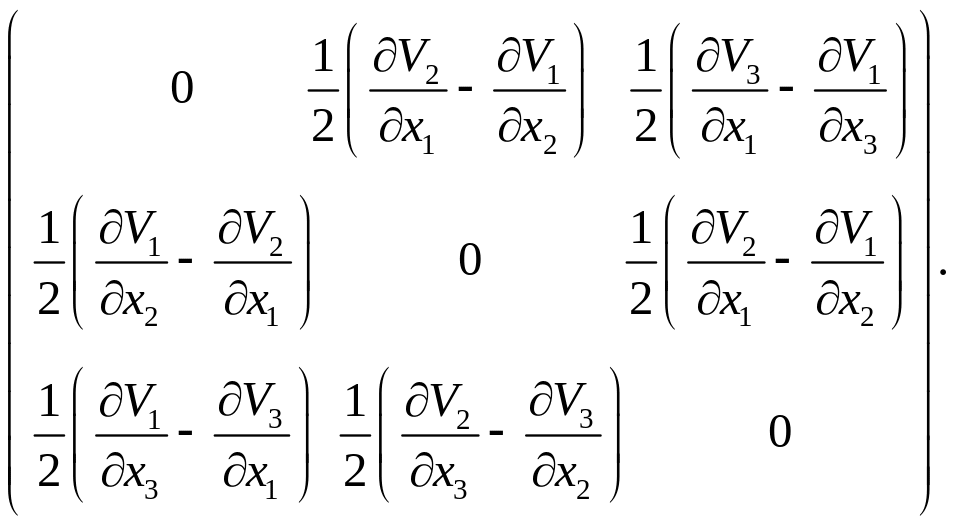
Она является матрицей компонент антисимметричного тензора .
Нетрудно заметить:
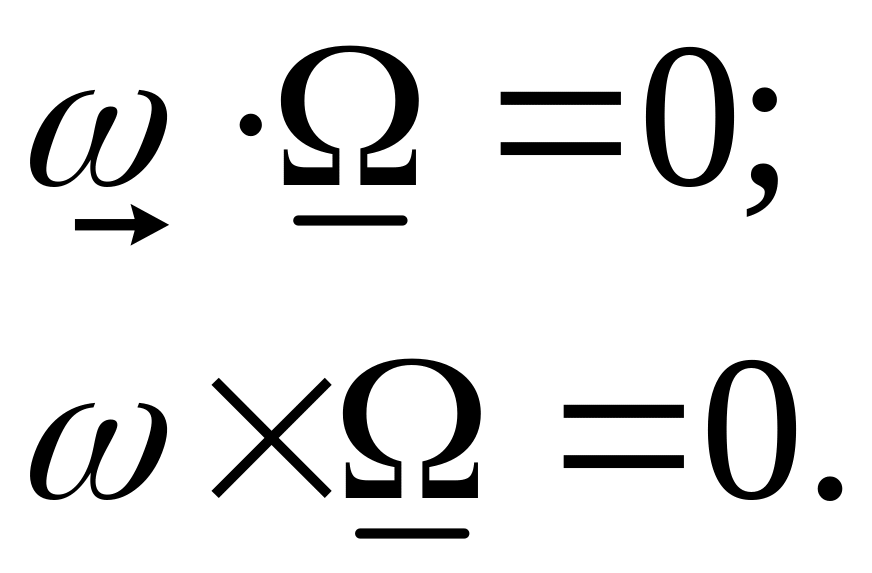
Действительно:
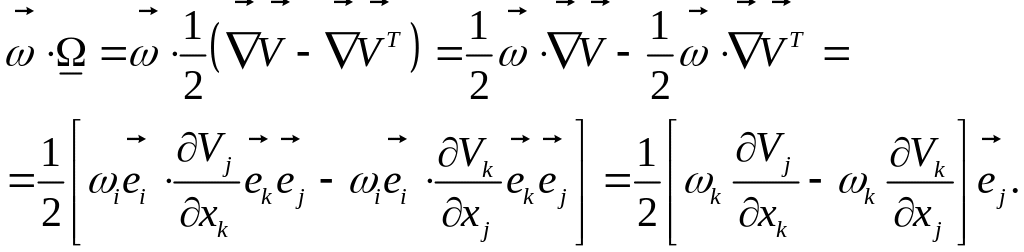
При
имеем проекцию на ось
:
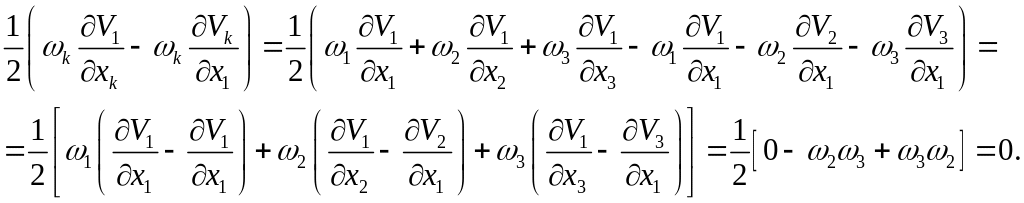
Аналогичным образом
можно заметить, что нулями будут и
выражения при
и
.
Равенство
следует из того, что
и
являются ассоциированными:
Кроме того справедливо равенство:
Действительно:
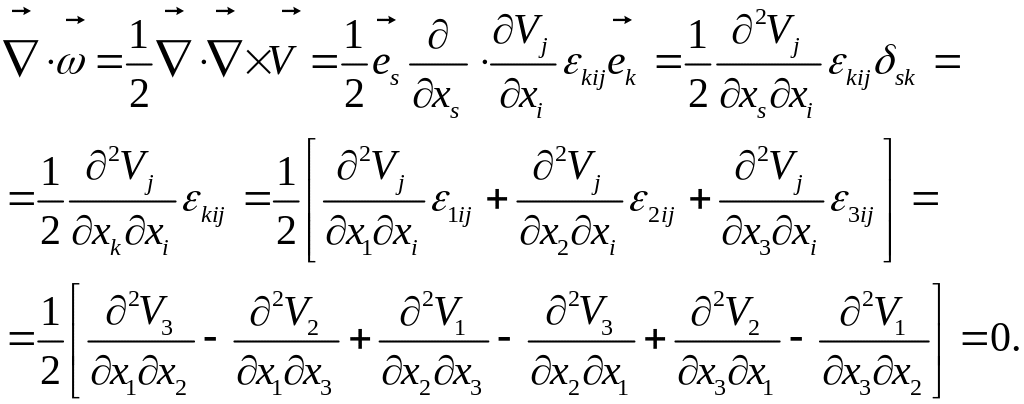
Ротор конвективного ускорения жидкой частицы может быть представлен в виде:
Доказательство справедливости этого соотношения можно выполнить, записывая конвективное ускорение по формуле И.С. Громеки.
Величина в этом выражении – вихрь:
Градиент вихря есть тензор второго ранга:
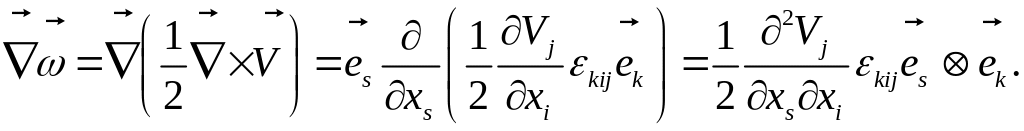
След этого тензора
,
в чем легко убедиться после несложных
выкладок.
Можно выделить симметричную и антисимметричную части этого тензора:
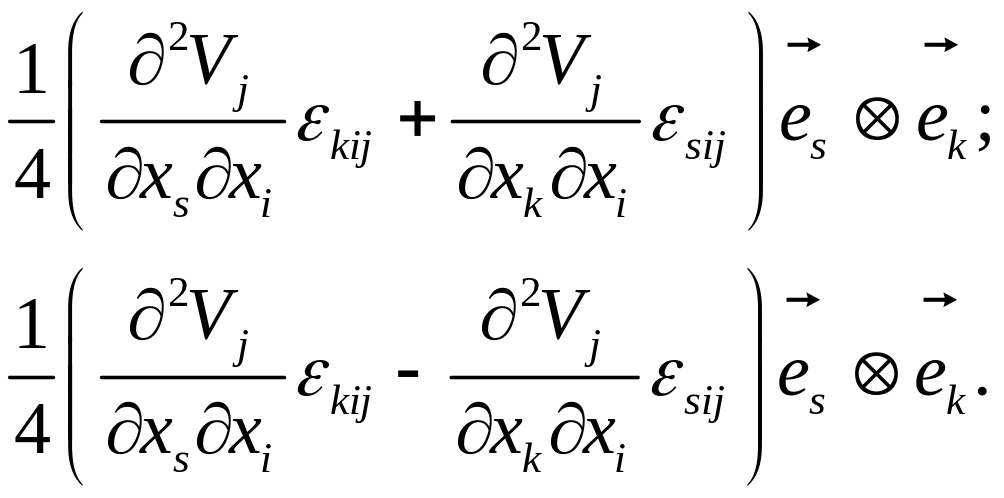
Применим операцию
ротора, операцию
к уравнению Навье-Стокса, которое можно
для случая движения несжимаемой жидкости
и условия потенциальности массовых сил
представить, используя формулу Громеки,
в виде (при
):
Применим к правой и левым частям:
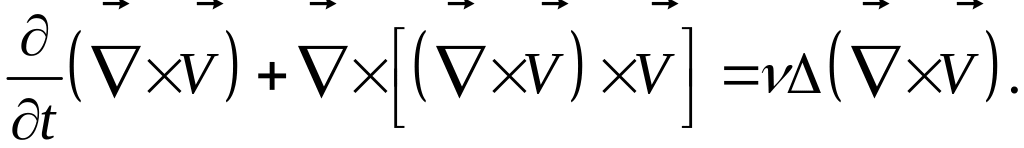
Второе слагаемое в левой части здесь можно представить в виде:
или, учитывая что
,
а жидкость несжимаема, т.е.
,
это слагаемое окончательно записывается
как:
Тогда получаем
уравнение переноса вихрей, учитывая
что
:
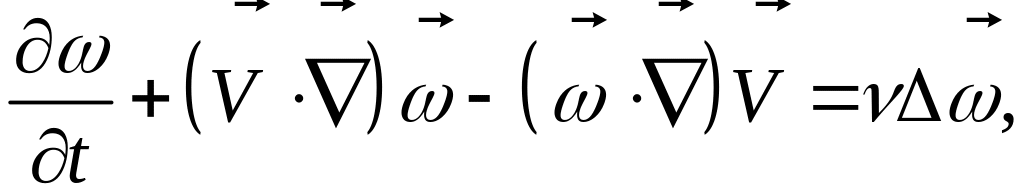
или, в компактном виде:
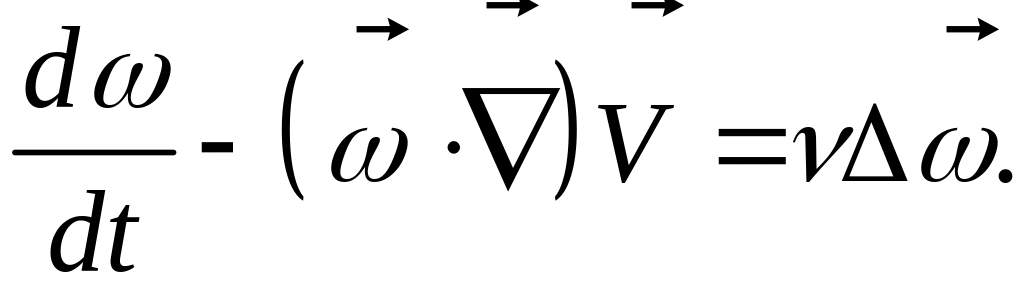
Для сжимаемой жидкости и при это уравнение усложняется. Уравнение переноса вихрей можно записать и по-другому, учитывая равенство:
Тогда:
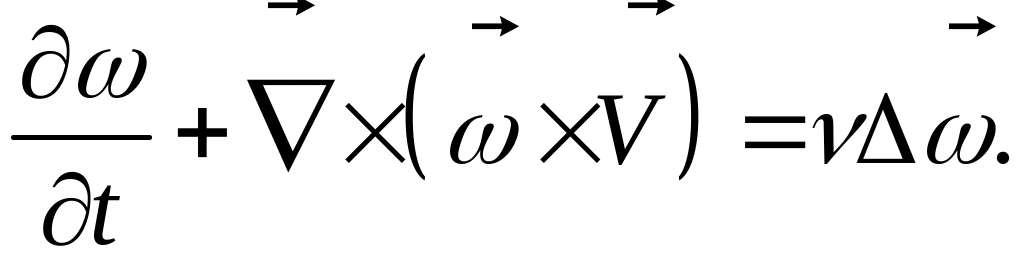
Если применить операцию дивергенции к уравнению переноса вихрей, то получаем:
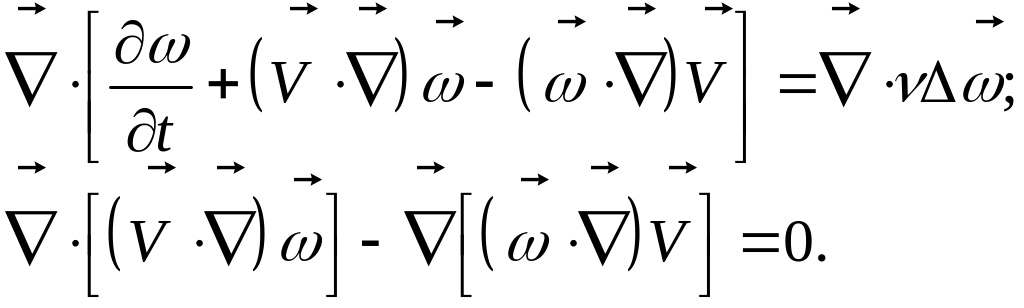
Но
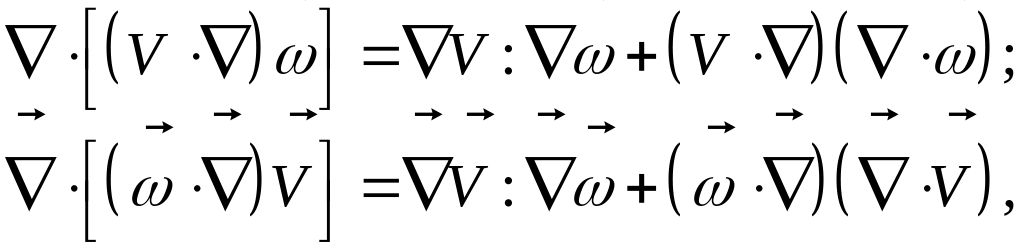
в результате
получаем
,
т.е. эта операция не дает нового
соотношения.
Для квадрата угловой скорости полезно соотношение
Если уравнение переноса вихрей скалярно умножить на :
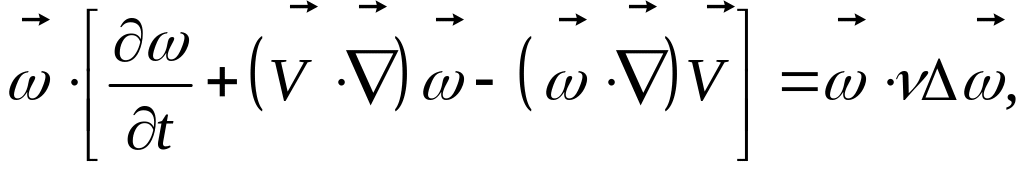
то получим скалярное
уравнение переноса
:
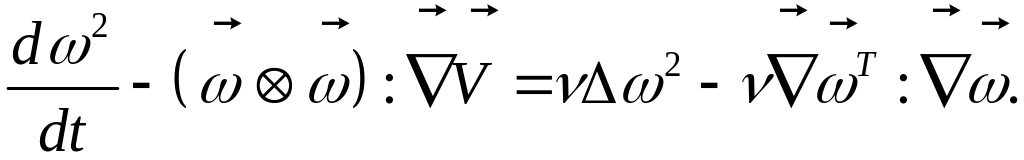
Очевидные равенства:
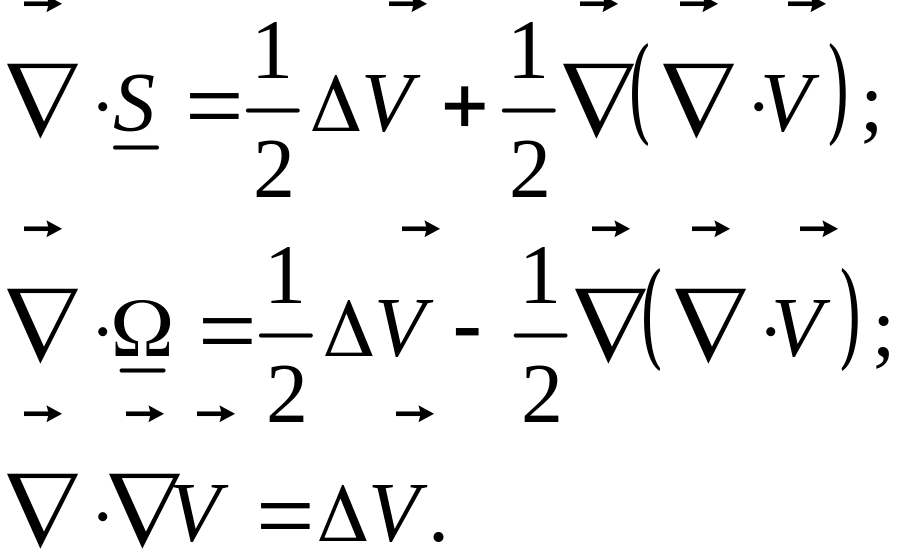
Для несжимаемой
жидкости
.
Поскольку:
то формулу Громеко можно записать в виде:
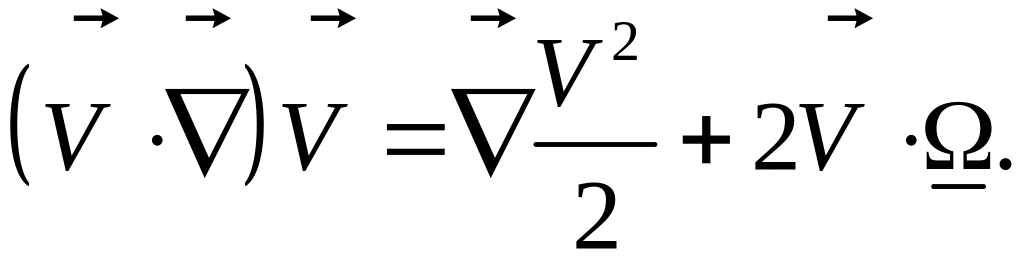
Запись ее в виде:
делает ее очевидной.
Запишем выражение:
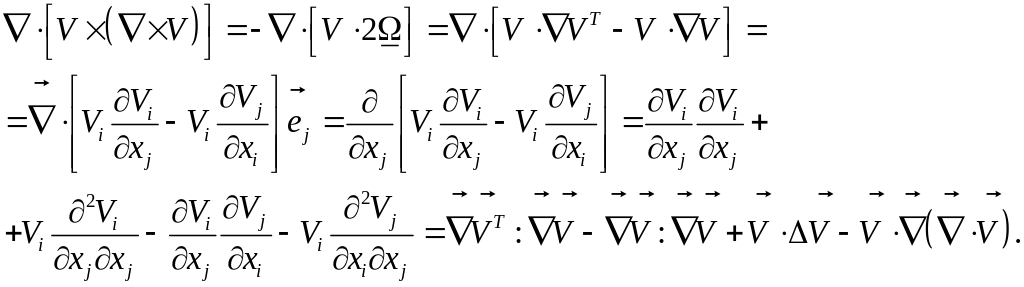
Таким образом
Эту формулу можно записать и по-другому:
или
Еще формула из очевидного равенства:
Отсюда
Но
,
следовательно
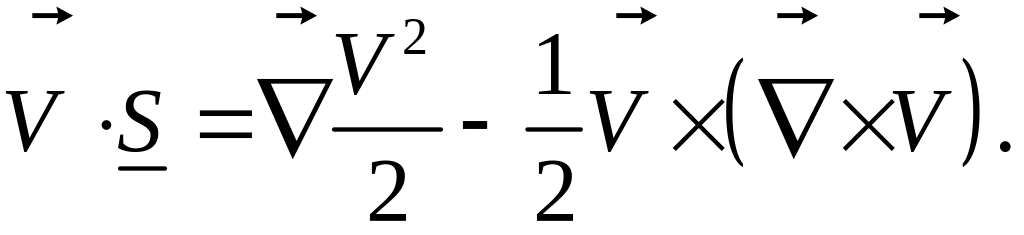
Векторное произведение градиентов скалярных функций дает вектор в виде ротора некоторой вектор-функции:
Действительно, левая часть этого равенства есть вектор:
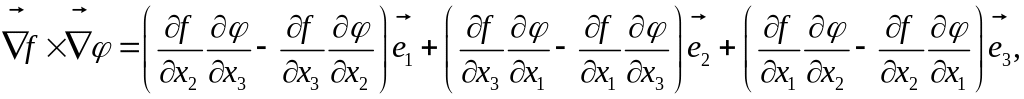
а правая часть дает:
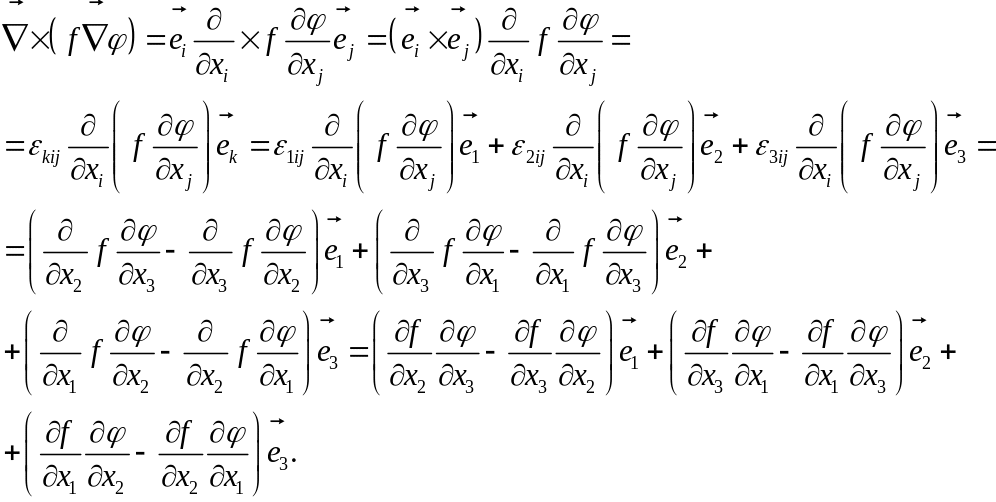
Отсюда видна справедливость этого равенства. Для векторного произведения градиентов скалярных функций справедливы также равенства:
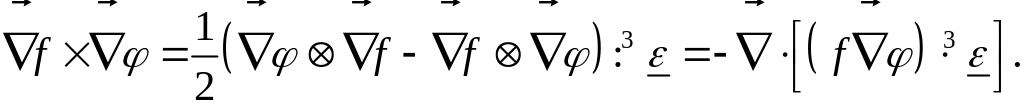
Для примера распишем последнее выражение в компонентной форме:
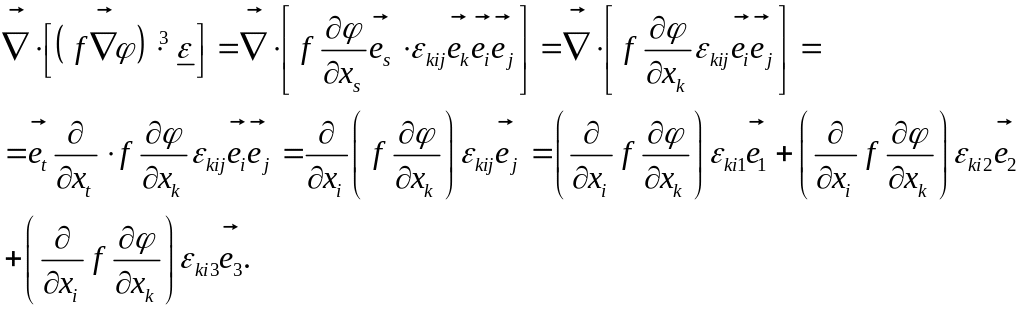
Видно, что знак
«минус» дает величину, совпадающую с
.