1.5 Инварианты тензоров и тензорные поверхности.

В тензорной алгебре особый интерес представляют скалярные функции тензорного аргумента, так называемые инвариантные, не зависящие от координат, тензорные функции. Рассмотрение простейших операций над тензорами показывает, что инвариантными скалярными функциями, в частности, являются:

здесь – векторы, – тензоры второго ранга, – единичный тензор. Очевидно, что . Это двойная свертка тензора второго ранга с метрическим называется следом тензора и обозначается :

(1.5.1)

Легко показать, что операция взятия следа тензора является линейной, т.е.:

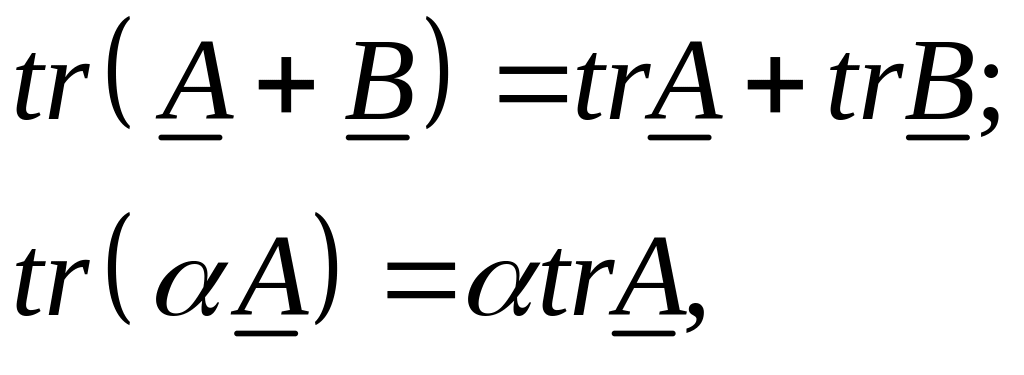
и имеют место следующие свойства следа:

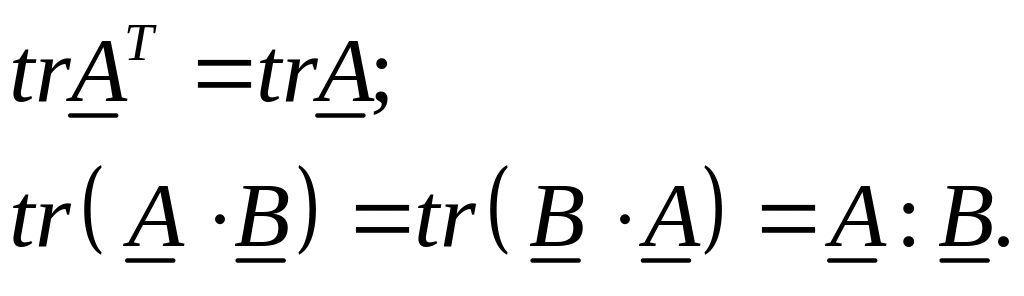
Замечание. Модуль тензора определяется в виде

Практический метод вычисление следа тензора:

(1.5.2)

Здесь учтено, что по определению дельты Кронекера следует равенство индексов . Аналогичным образом можно получить

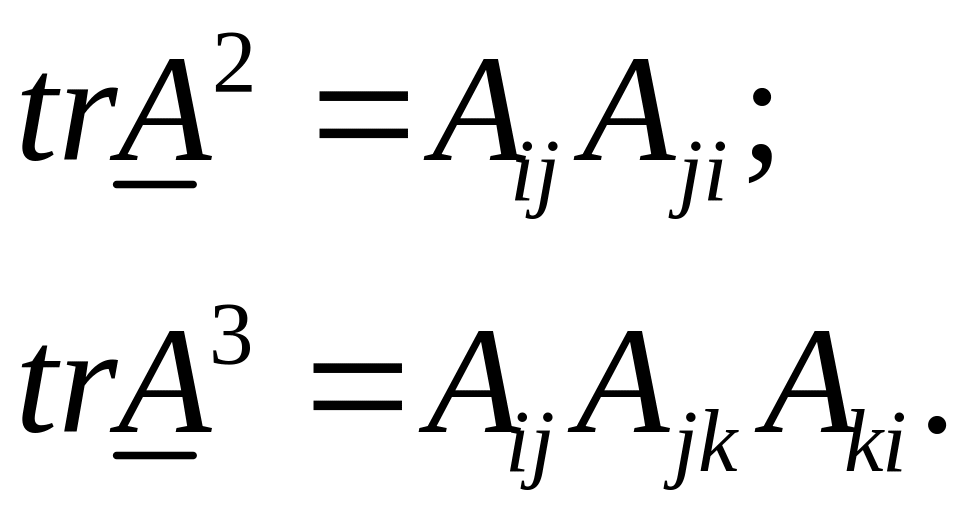
Видно, что след тензора – сумма диагональных компонент этого тензора.

Пример. Вычислим след тензора, компоненты которого образуют матрицу.

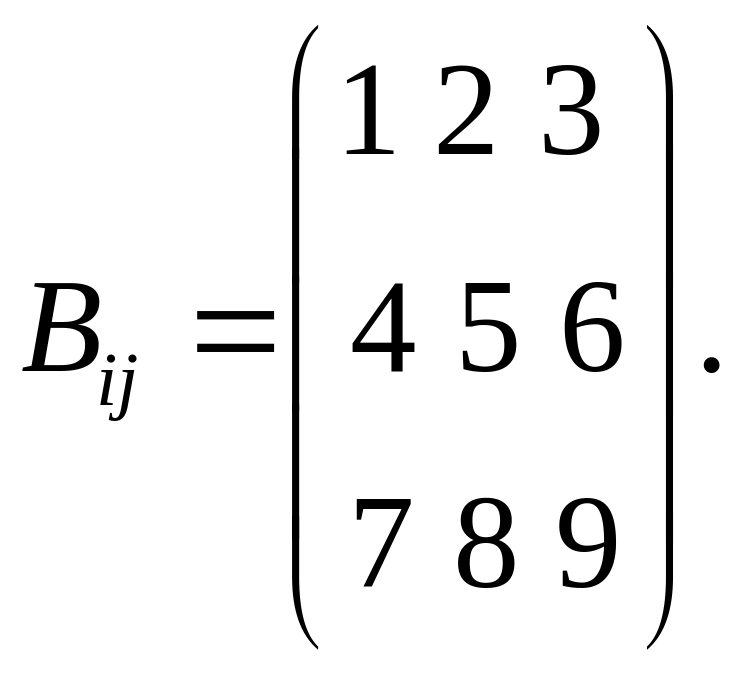
Отметим, что любая скалярная функция инвариантов будет также инвариантной скалярной функцией тензора. В частности, для характеристики тензора второго ранга используют следующие три скалярные функции, называемые соответственно первым, вторым и третьим инвариантами тензора :

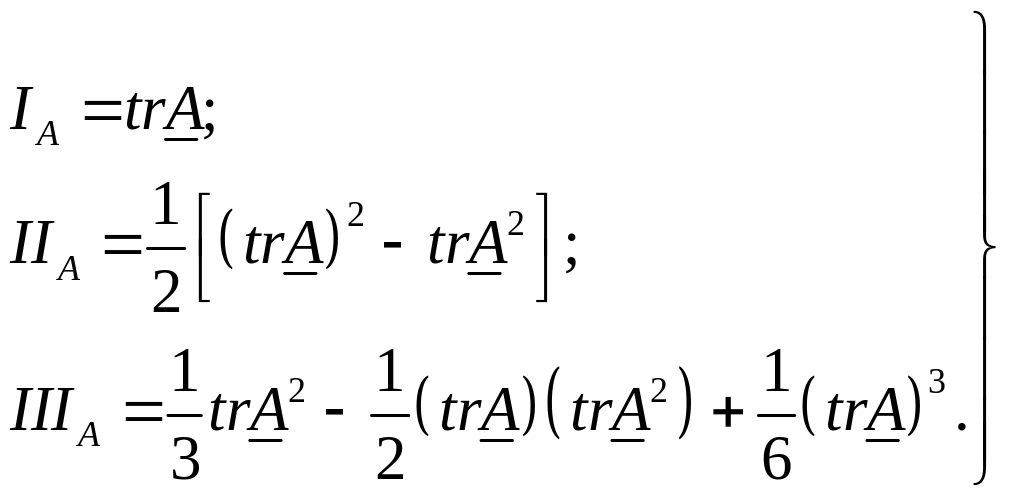(1.5.3)

Можно показать, что третий инвариант , где – детерминант матрицы компонент тензора в произвольном базисе.

Функции называются главными инвариантами тензора . Они играют чрезвычайно важную роль в тензорной алгебре из-за следующей теоремы представления симметричных тензоров второго ранга: любая инвариантная скалярная функция симметричного тензорного аргумента может быть представлена как функция трех главных инвариантов этого аргумента, т.е.:

Главные инварианты используются также в таком полезном тождестве, соотношение Гамильтона-Келли:

(1.5.4)

которое можно применять, например, при вычислении любых целых степеней тензора .

Пример. Пользуясь теоремой Гамильтона-Келли, вычислим для тензора , который в прямоугольной декартовой системе координат имеет следующие компоненты:

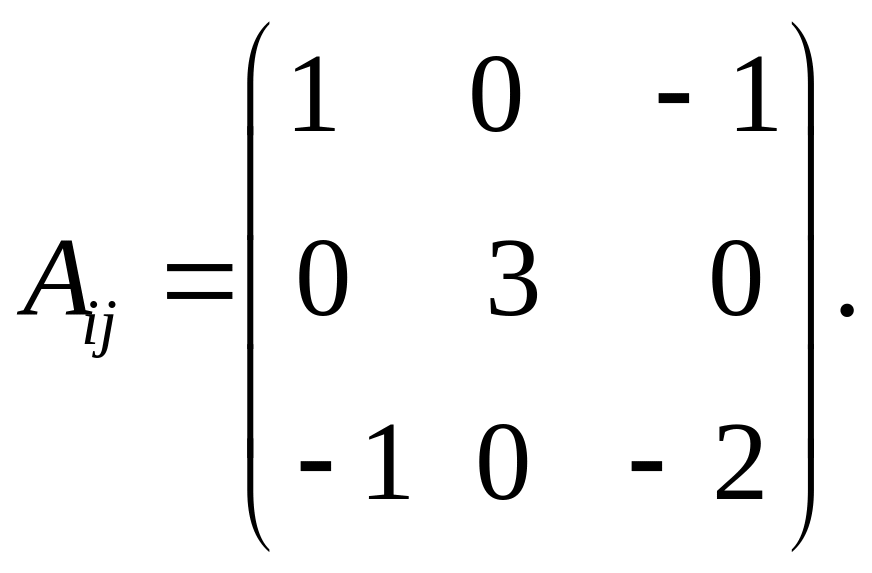
Для начала определим , а затем главные инварианты тензора по формулам :

Умножим тождество Гамильтона-Келли скалярно на и запишем следующее выражение относительно :

Выражая отсюда и используя для соотношение Гамильтона-Келли, имеем

Отсюда в выбранном базисе:

Вычисляя как произведение соответствующих матриц:

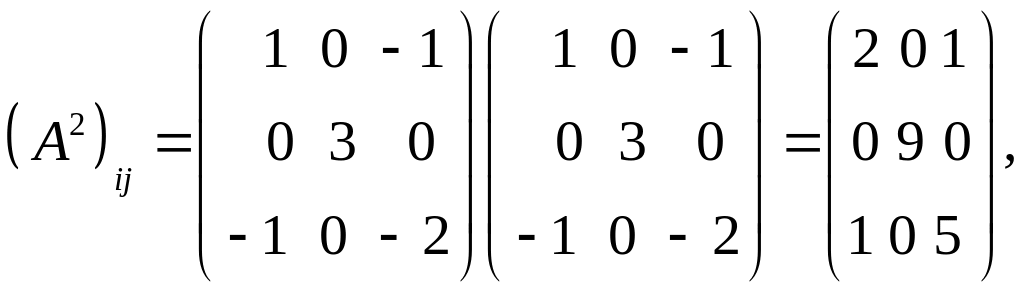
окончательно имеем:

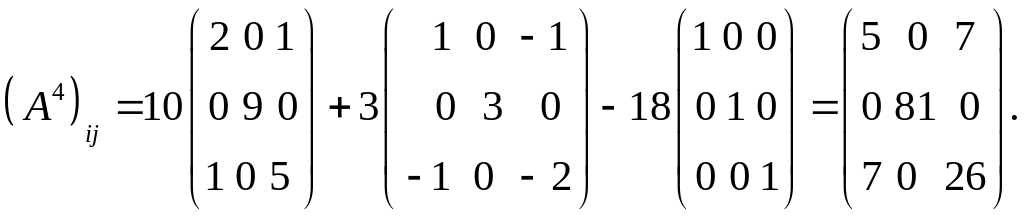
Пример. Вычислим второй инвариант тензора , равного сумме тензоров второго ранга:

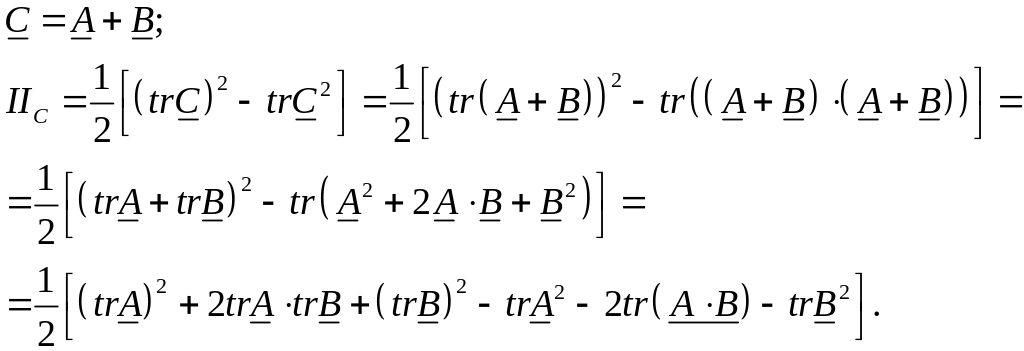
Рассмотрим теперь главные векторы и главные значения тензоров. Пусть имеется некоторый произвольный симметричный тензор второго ранга . Из тензорной алгебры [9, 19] известно, что если для ненулевого вектора и тензора второго ранга выполнено условие:

(1.5.5)

то вектор называется главным (собственным) вектором тензора , соответствующее направление – главным направлением (главной осью) тензора , а число – главным (собственным, характеристическим) значением тензора . Равенство (1.5.5) можно записать как

(1.5.6)

или в компонентной форме:

(1.5.7)

Система этих трех однородных линейных алгебраических уравнений имеет ненулевое решение, если

(1.5.8)

Раскрывая (1.5.8) , получаем характеристическое уравнение для тензора

(1.5.9)

где – инварианты тензора , которые можно вычислить по формулам (1.5.3). Решение кубического уравнения (1.5.9) дает три корня , которые являются вещественными, поскольку матрица в выражении (1.5.8) симметрична. Эти корни являются главными значениями тензора . В принципе каждому значению соответствует свой главный вектор , компоненты которого находятся из решения уравнений (1.5.7). В результате получаем три главных вектора . Заметим, что главные векторы, отвечающие различным значениям , взаимно ортогональны, что непосредственно следует из (1.5.5).

Вообще говоря, в отношении чисел , являющихся корнями уравнения (1.5.9) (а следовательно, и векторов ), могут возникнуть следующие ситуации:

1) , тогда тройка векторов определяется однозначно;

2) , однозначно определяется лишь , в качестве и можно брать любые два взаимно-ортогональных вектора, которые перпендикулярны ;

3) , в качестве можно брать любую взаимно-ортогональную тройку векторов. Тензоры, для которых это имеет место, называются шаровыми. Они имеют вид , .

Замечание 1. В качестве базисных векторов для тензора можно взять тройку ортонормированных главных векторов . Тогда

(1.5.10)

Пример 1. Тензор напряжений в некоторой точке в прямоугольной декартовой системе координат имеет компоненты

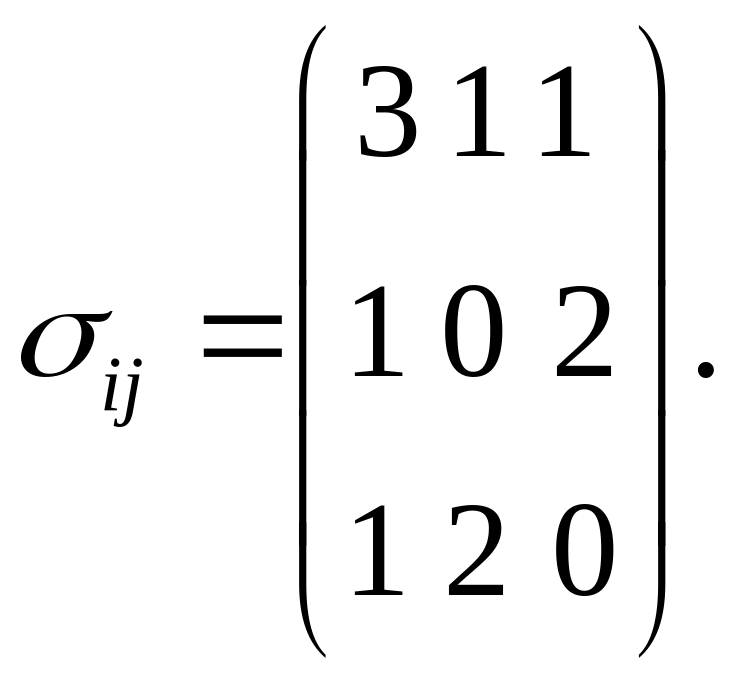
Определим главные напряжения (главные значения тензора ) и главные оси тензора напряжений.

Согласно (1.5.8) главные напряжения определяются из уравнения

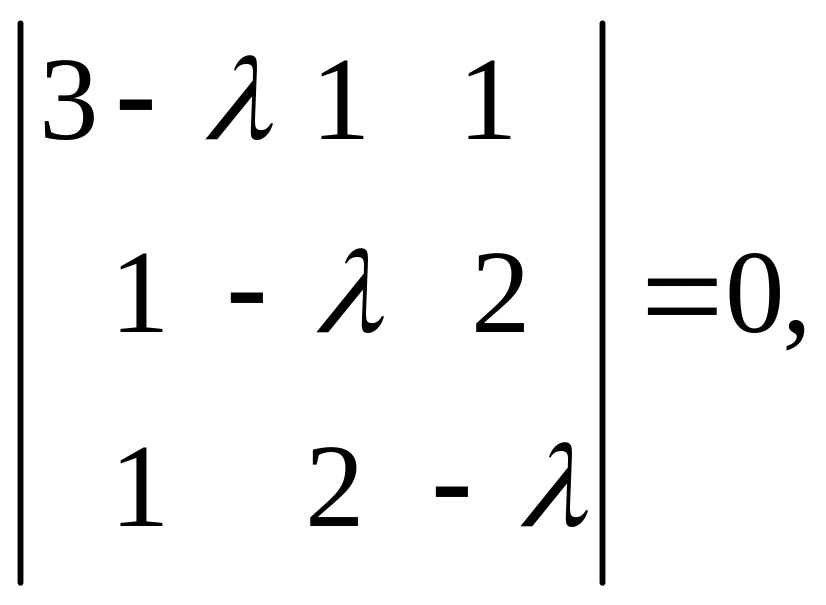
или после раскрытия определителя:

Корни этого уравнения и будут являться главными напряжениями: , , .

Главные направления тензора определим следующим образом. Пусть каждому главному направлению соответствует своя ось новой системы координат . Для каждой из таких новых осей введем в рассмотрение и определим направляющие косинусы этих осей относительно старых . Так, пусть главному значению соответствует ось с направляющими косинусами . Тогда согласно (1.5.7)

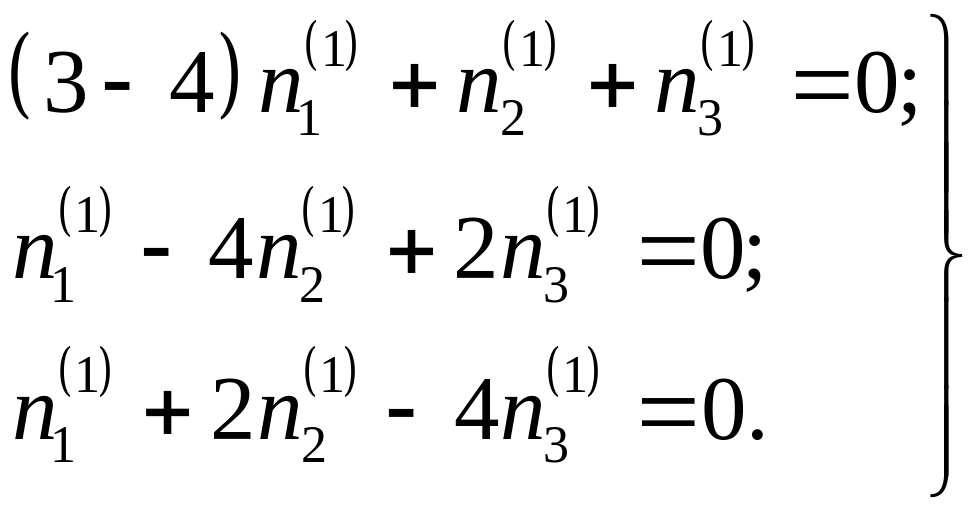
Отсюда, учитывая, что , получаем

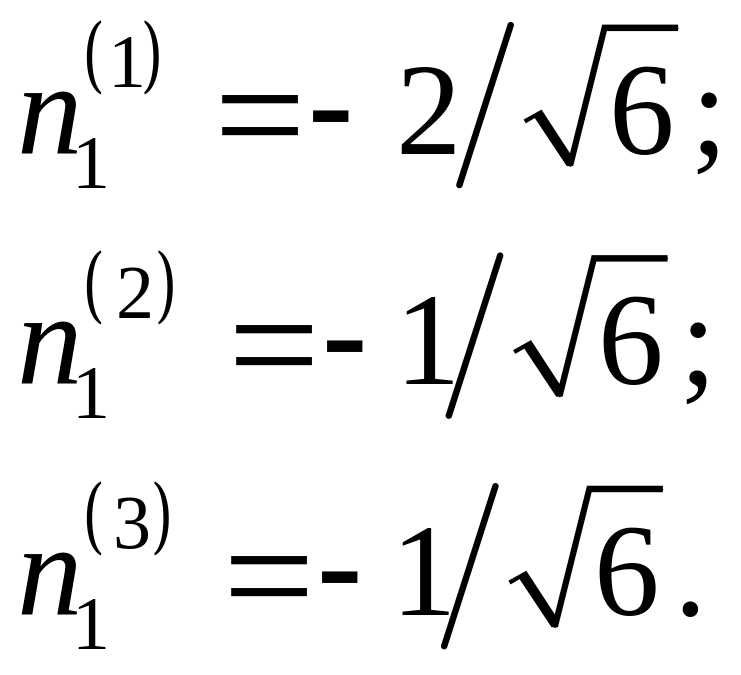
Аналогично можно составить системы уравнений для определения направляющих косинусов и , связанных с осями и , соответствующих главным значениям и . В результате получаем (проверить самостоятельно)

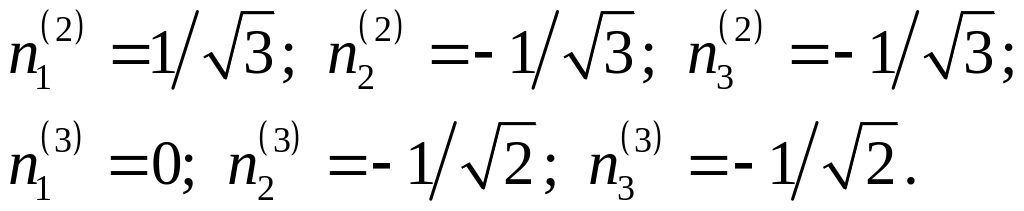
Вектором симметричного тензора по площадке с еденичной нормалью является вектор напряжений (рис. 1.9). Составляющая этого вектора по направлению нормали называется нормальной составляющей:

Вторая составляющая этого вектора лежит в плоскости площадки и имеет направление, определяемое некоторым единичным вектором (очевидно, ):

Эта составляющая является касательной составляющей вектора . В литературе нормальную составляющую вектора напряжений называют нормальным напряжением, а касательную – касательным напряжением (часто их величины обозначают как и соответственно).

Рис. 1.9. Разложение вектора тензора на нормальную и касательную составляющие.

Если сформулировать и решить задачу об условном экстремуме на всех еденичных нормалях , то результат будет следующим: экстремальные значения как раз равны главным значениям тензора , а именно . Нормали, на которых достигаются экстремумы, имеют направления главных направлений тензора . В этом случае касательные напряжения .

Экстремальные значения достигаются в плоскостях, которые биссектральны по отношению к плоскостям, нормальным к главным осям тензора. Они равны

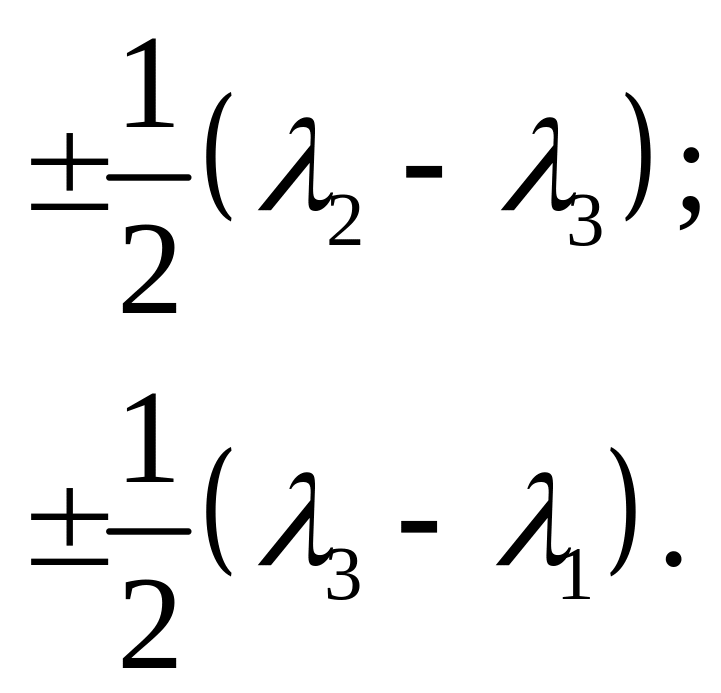
Нормальные напряжения по этим плоскостям в общем случае не являются нулевыми.

Пример 2. Тензор напряжений в некоторой точке в прямоугольной декартовой системе координат имеет компоненты

Пусть в этой точке имеется площадка с единичным вектором , где – базисные векторы (в данном случае это суть векторы ). Найдем вектор напряжения в этой точке и нормальную составляющую этого вектора.

Вектор напряжения или в компонентной форме записи . Отсюда

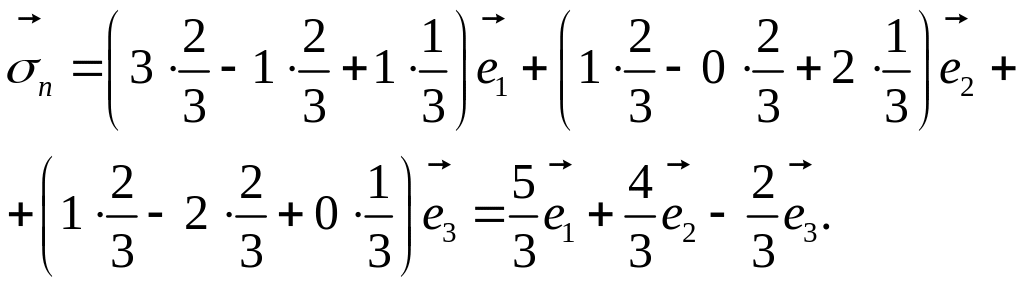
Нормальная составляющая этого вектора или в компонентной форме . Отсюда . Следовательно, вектор имеет лишь касательную составляющую .

Упражнение. Определить величины главных значений для тензоров, которые в декартовой прямоугольной системе координат имеют компоненты

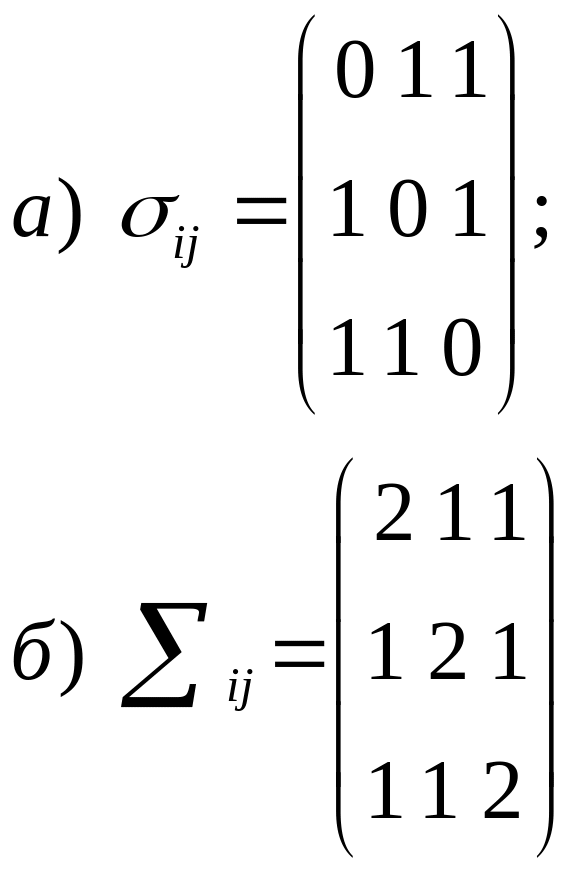
и показать, что главные оси этих тензоров совпадают.

Если в качестве базисных векторов для взять тройку главных векторов , то этот тензор будет лишь иметь компоненты

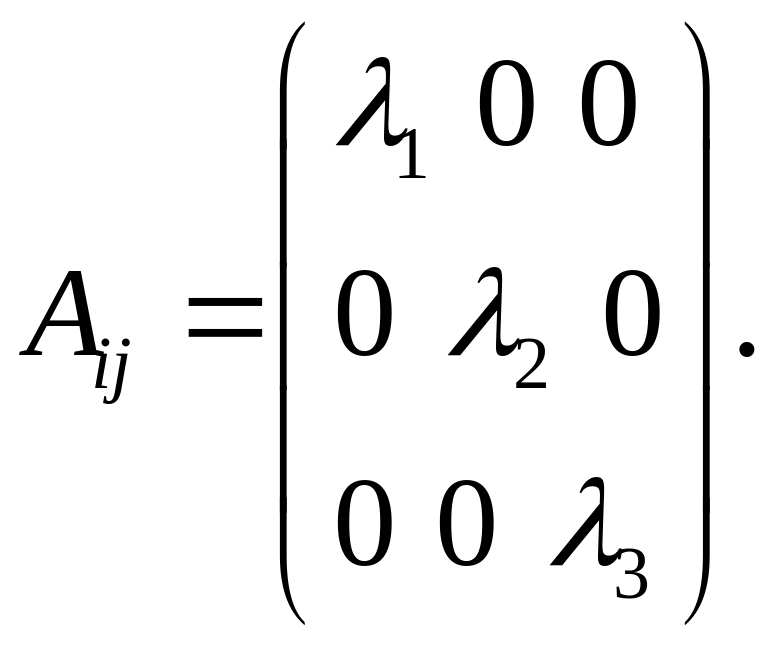
Главные варианты тензора выражаются через собственные числа следующим образом (исходя из формул (1.5.6)):

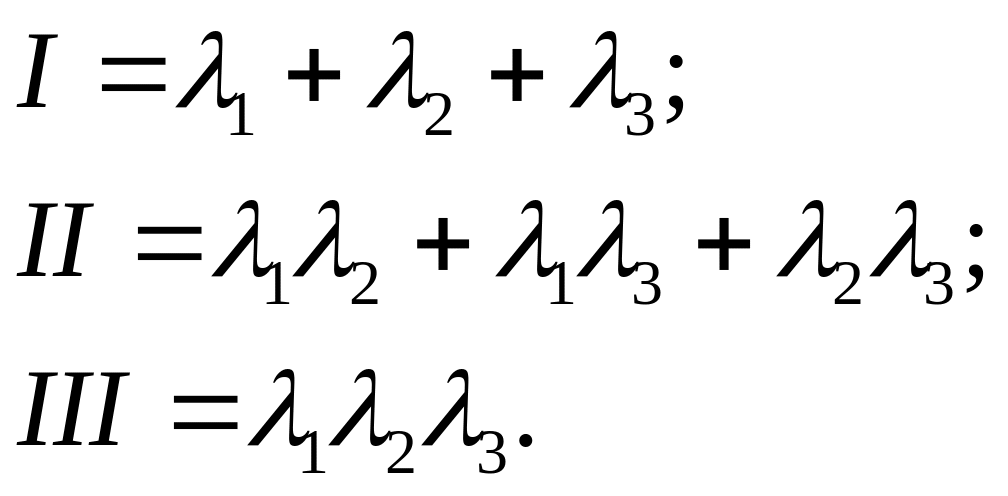(1.5.10)

В компонентной форме такой тензор имеет вид

Полезными являются следующие соотношения:

(1.5.11)

в справедливости которых легко убедиться.

Замечание 2. Если тензор обладает простым спектром, то его характеристическое уравнение можно записать в виде

Соответствующий ему минимальный многочлен

после раскрытия дает тождество

Учитывая (1.5.11), приходим к соотношению Гамильтона-Кэлли (1.5.4), позволяющему сводить степени тензора до степеней не ывше второй:

(1.5.12)

Интересно заметить, что для осесимметричного тензора и вторую степень тензора можно свести к первой. В самом деле, для такого тензора два собственных числа одинаковы (например, ) и его характеристическое уравнение имеет вид

или

Минимальный многочлен

после элементарных преобразований приводит к выражению

(1.5.13)

Таким образом, вместо соотношения Гамильтона-Кэлли для осесимметричного тензора имеет место соотношение, позволяющее выразить вторую степень тензора через первую:

Замечание 3. Из тензора, обладающего простым спектром, всегда можно получить после некоторых операций над ним тензор с осесимметричным спектром или шаровой. Например, пусть имеется тензор с неравными между собой собственными числами :

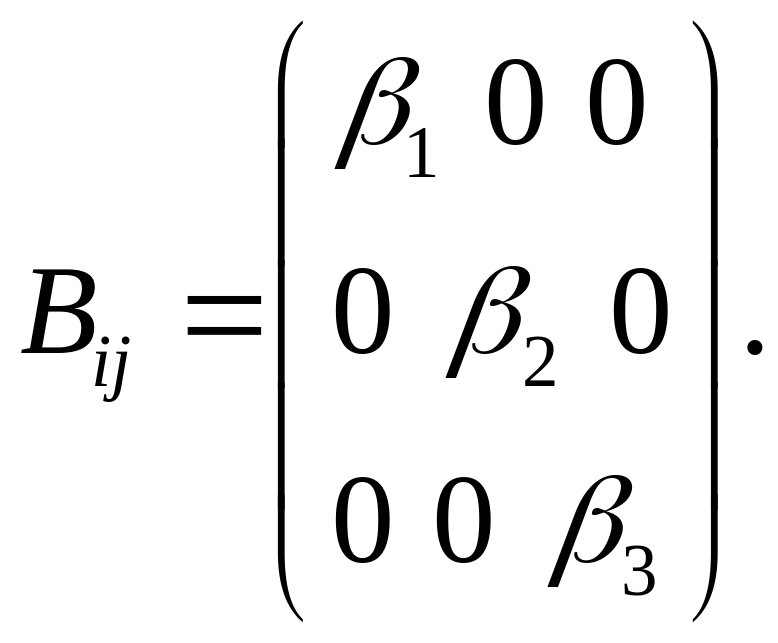
Шаровой тензор получается элементарно после взятия следа тензора :

(1.5.14)

Осесимметричный тензор можно получить так:

(1.5.15)

Действительно,

где

Видно, что тензор – осесимметричный. Осесимметричным будет и тензор

(1.5.16)

Его собственные числа

Очень часто бывает полезным разложить тензор на шаровую и девиаторную части:

где – шаровая часть тензора ; ; – девиатор тензора ; . Очевидно, что главные оси девиатора совпадают с главными осями тензора .

Пример 3. Тензор напряжений в некоторой точке в выбранном базисе имеет компоненты

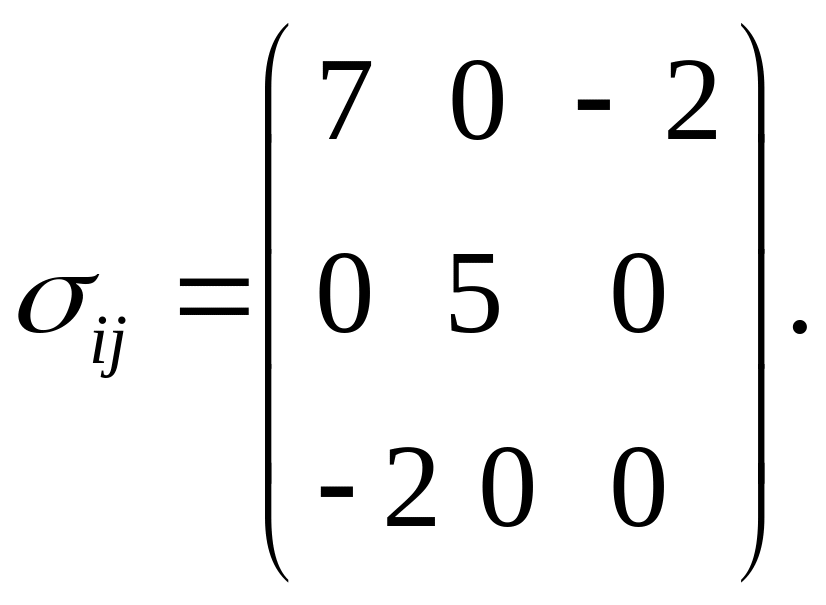
Выделим шаровую и девиаторную части. Поскольку , то

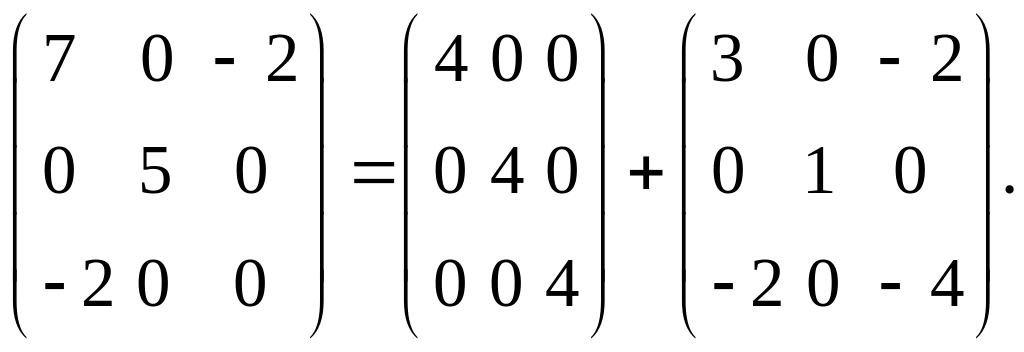
Упражнение. Выделим шаровую и девиаторную части тензора, приведенного в примере 2 данного параграфа.

Для наглядной интерпретации симметричного тензора второго ранга используют некоторую поверхность второго порядка, задаваемую уравнением:

(1.5.17)

ТО, что это уравнение поверхности второго порядка можно увидеть записывая левую часть этого равенства в терминах компонент:

или более подробно, суммируя сначала по , затем по :

В результате имеем уравнение поверхности, учитывая что для симметричного тензора :

или, в обычных обозначениях:

(1.5.18)

Эта квадратичная форма является уравнением поверхности эллипсоида, который называется тензорным эллипсоидом для тензора в рассматриваемой точке среды. Коэффициентами этой формы служат компоненты тензора . На рисунке 1.10 показан тензорный эллипсоид, построенный в некоторой точке для тензора .

Рисунок 1.10 – Тензорный эллипсоид.

Главные оси тензора совпадают с направлениями главных векторов этого тензора. Два тензора называются соосными, если главные оси их тензорных эллипсоидов совпадают. Очевидно, что при тензорный эллипсоид есть эллипсоид вращения, а при тензорная поверхность является сферой (шаровому тензору соответствует поверхность сферы).

Часто используют для тензора напряжений и кинематического тензора приведенные выше понятия главных векторов и главных значений тензоров, а также наглядную их интерпретацию с помощью понятия тензорного эллипсоида. Можно говорить об эллипсоиде напряжений и эллипсоиде деформаций (или скоростей деформаций).

Полезно заметить, что для всякого симметричного тензора второго ранга все его собственные числа вещественны. Говорят, что тензор имеет простой спектр, если среди его собственных чисел нет кратных, т.е. все они различны. При этом триэдр главных (собственных) направлений, определяемый главными (собственными) векторами , определяется однозначно (с точностью до ориентации, связанной с различием правых и левых троек векторов). Тензорная поверхность для этого случая, когда нет нулевых собственных чисел, схематично показана на рисунке 1.11а. Симметричный тензор называют осесимметричным, если два его собственных числа совпадают, но не равны третьему. В этом случае однозначно определено лишь одно собственное направление, а в нормальной плоскости любое направление является собственным. Соответствующая ему тензорная поверхность, являющаяся эллипсоидом вращения в общем случае, показана на рисунке 1.11б. Для шарового тензора все собственные числа одинаковы, и он с точностью до множителя совпадает с единичным. Все направления в пространстве для него являются собственными. Соответствующая тензорная поверхность (сфера) показана на рисунке 1.11в. Вырожденные поверхности имеют место при наличии нулевых собственных чисел.

Рисунок 1.11 – Тензорные поверхности.

Вообще говоря, в качестве инвариантов тензора могут быть взяты любые другие три скалярные величины, являющиеся функциями от инвариантов I, II, III или, что то же самое, от главных нормальных напряжений , являющихя корнями характеристического уравнения. В частности, используется и система инвариантов , в которой первый, второй и третий инварианты определяются как

(1.5.19)

Связь этих инвариантов с инвариантами выражается элементарными формулами. Очевидно .

Первый инвариант тензора напряжений может быть представлен явным образом через компоненты:

Из сравнения этой формулы с формулой (7.1.16????) следует:

(1.5.20)

Отсюда виден физический смысл первого инварианта тензора напряжений – он характеризует среднее нормальное напряжение.

Второй и третий инварианты для систем инвариантов и не имеют ясного физического смысла. В этом отношении предпочтительна для анализа поведения сплошной среды система инвариантов , предложенная В.В. Новожиловым [7, 8,17], которая имеет ясный физический смысл:

(1.5.21)

В этих формулах – главные нормальные напряжения (причем ); – первый инвариант тензора напряжений, характеризующий среднее нормальное напряжение; – второй инвариантхарактеризующий среднее касательное напряжение в рассматриваемой точке; – третий инвариант (угол вида), характеризующий отношение среднего и максимального касательного напряжений. Эта физическая интерпретация угла вида также дана в работе [7].

Примечание 6. Среднее касательное напряжение определяется согласно [6] следующим образом:

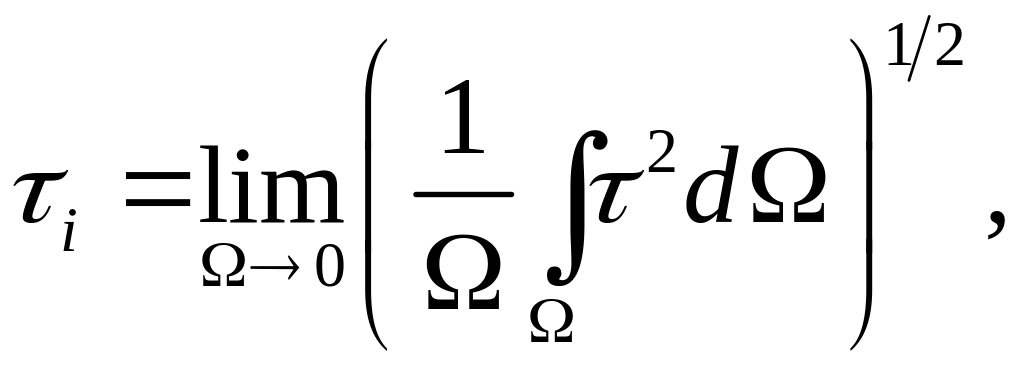
где – касательное напряжение, действующее на элементарную площадку ; – площадь поверхности, ограничивающей элементарный объем. Максимальное касательное напряжение, как это видно из рисунка 1.11, определяется формулой:

Возможно и чисто геометрическая интерпретация угла вида (рисунок 1.12). Рассмотрим сечение эллипсоида напряжений плоскостью, проходящей через главные оси, соответствующие и . Это сечение изображено на рисунке 1.12 сплошной линией. Здесь эллипс с центром в точке и главной осью проведен через две точки и , соответствующие нормальным напряжениям и . На площадках, где действуют и , касательные напряжения равны нулю. Теперь предположим, что по каким-либо причинам на этих площадках все же возникло касательное напряжение . Тогда рассмотренные выше напряжения уже не будут главными, и произойдет трансформация эллипса и поворот его относительно главной оси , которая сохраняется, на некоторый угол в плоскости чертежа. Направление новой главной оси показано на рисунке 1.12 пунктирной линией . Возникает новый эллипс, проходящий через точки 1 и 2, который также обозначен пунктиром. Можно показать методами аналитической геометрии, что через точки 1 и 2 можно провести эллипс с центром в точке 0 только льшь при условии, что . Можно также показать, что предельное, наибольшее значение этого угла при фиксированных точках 1 и 2 для данного центра 0 и есть угол вида, определяемый формулой (1.5.20), т.е. . Отсюда ясна чисто геометрическая интерпретация угла вида – это тот максимальный угол, на который повернулась бы главная ось эллипсоида напряжений, если бы на данной площадке, ориентация которой связана с главной осью тензора, внезапно возникли бы касательные напряжения. Величина этих дополнительных касательных напряжений не может превосходить некоторой предельной величины.

Рисунок 1.12 – Угол вида.

Если инварианты и известны, то главные напряжения можно вычислить по формулам:

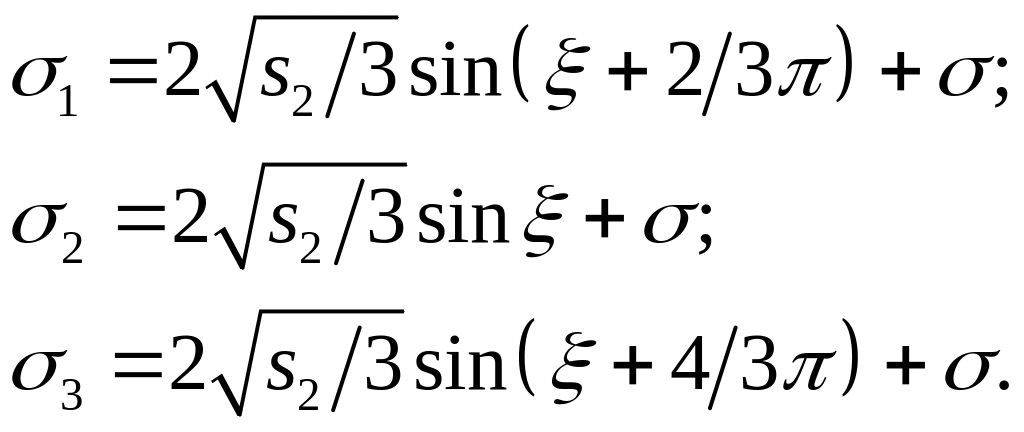(1.5.22)

Интересно отметить, что среднее касательное и максимальное касательное напряжения связаны между собой через угол вида

(1.5.23)