5.3. Класична регресія

Регресійна модель описує об’єктивно існуючі між явищами кореляційні зв’язки. За своїм характером кореляційні зв’язки над­звичайно складні та різноманітні. В одних випадках результат у зі зміною фактора х_і зростає чи зменшується рівномірно, в інших — нерівномірно. Іноді зростання може змінитися зменшенням і навпаки. Простежити всі ці взаємозв’язки і встановити точний функціональний вид практично неможливо. А тому при виборі типу функції йдеться лише про апроксимацію відносно простими функціями незрівнянно більш складних за своєю природою взаємозв’язків. На практиці перевагу віддають моделям, які є лінійними або приво- дяться до лінійного виду шляхом перетворення змінних, наприклад логарифмуванням. Такий підхід, безперечно, містить у собі певну умовність, оскільки передбачає однаковий характер зв’язку з усіма факторами. Проте використання надто складних функцій неминуче веде до збільшення кількості параметрів, а отже, зменшує точність вимірювання та ускладнює інтерпретацію результатів.

При обґрунтуванні типу функції слід враховувати й той факт, що межі варіації корельованих ознак у конкретних умовах простору і часу, в конкретній сукупності значно вужчі за їх можливі значення, і в цих межах варіації навіть лінійна функція може задовільно апроксимувати зв’язок.

У лінійному щодо параметрів рівнянні регресії індивідуальне значення результативного показника у_j (де j — порядковий номер одиниці сукупності) записується так:

,

де b₀ — вільний член рівняння; економічного змісту, як правило, не має, лише окреслює область існування моделі;

b_і — коефіцієнт регресії; показує, як в середньому змінюється у зі зміною х_і на одиницю її шкали вимірювання за незмінності інших включених в модель факторів і за інших рівних умов;

e_{j =} y_j – Y_j — залишкова величина.

У регресійній моделі основне навантаження покладається на коефіцієнт регресії b_і, він розглядається як своєрідна міра «очищеного» впливу х_і на у і називається ефектом впливу.

Процедура оцінювання параметрів регресійної моделі ґрунтується на методі найменших квадратів (МНК). Оскільки алгоритми МНК описано в математико-статистичній літературі й реалізовано в комп’ютерних програмах, наведемо лише загальну схему розрахунку статистичних характеристик моделі, акцентуючи увагу на їх змістовній інтерпретації.

Первинна інформація представляється як матриця факторних ознак Х розміром (n ∙ m) і вектора результативної ознаки у розміром (n ∙ 1). Задля зручності використання алгоритмів МНК матриця Х розширюється за рахунок додатково введеної фіктивної змінної х₀, вектор якої представлений одиницями. Параметри моделі — вектор В ₌ │b₀, b₁, b₂, …, b_m│ визначаються розв’я­зуванням системи нормальних рівнянь, яка записується так:

X′XB ₌ X′y, де X′X — матриця розміром n (m + 1).

Послідовність розрахунків включає етапи:

• обчислення матриці X′X і вектора X′y;

• обертання матриці C = (Х′Х)^–1;

• розрахунок параметрів B = CX′y;

• визначення теоретичних значень результативної ознаки 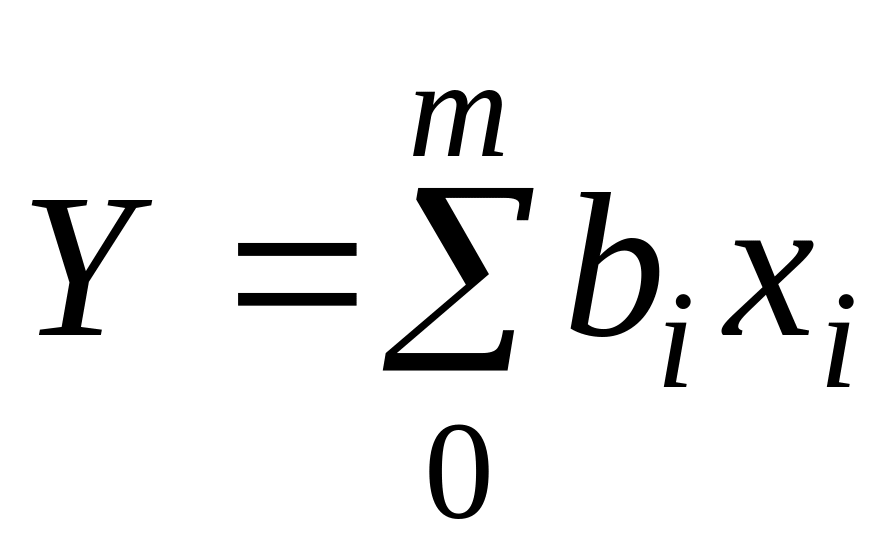та залишків e_j = y_j – Y_j .

Значення коефіцієнтів регресії певною мірою залежать від складу введених у модель факторів. З розширенням ознакової множини моделі відбувається перерозподіл впливу попередньо введених факторів. Чим вагоміший вплив нововведеного фактора, тим помітніші зміни. Ілюстрацією перерозподілу впливу факторів може слугувати регресійна модель урожайності рису, ц/га [11]. У модель послідовно вводились агротехнічні фактори: х₁ —попередник, балів; х₂ — внесення добрив під основний обробіток, центнерів поживної речовини (ц п. р.) на 1 га посіву; х₃ — передпосівний обробіток, га м’якої оранки; х₄ — підживлення, ц п. р.; х₅ — норма висіву; х₆ — кількість прополювань. Відповідно отримано такі рівняння регресії:

1. Y = 30,432 + 3,001х₁;

2. Y = 26,208 + 2,049х₁ + 5,995х₂;

3. Y = 21,563 + 1,970х₁ + 4,610х₂ + 2,906х₃;

4. Y = 22,332 + 1,321х₁ + 4,558х₂ + 1,465х₃ + 9,791х₄;

5. Y = 18,960 + 1,342х₁ + 4,483х₂ + 1,347х₃ + 9,545х₄ + 1,756х₅;

6. Y = 19,387 + 0,965х₁ + 3,400х₂ + 0,501х₃ + 7,500х₄ + 1,731х₅ + + 3,433х₆.

Як бачимо, введення кожного нового фактора спричиняє зменшення впливу попередньо введених факторів, таку ж тенденцію має й вільний член рівняння.

Оскільки факторні ознаки мають, як правило, різні одиниці вимірювання, то для порівняння ефектів їх впливу в рамках моделі використовують стандартизовані коефіцієнти регресії (бета-коефіцієнти) або коефіцієнти еластичності . Бета-коефіцієнт характеризує ефект впливу х_і на у в середньоквадратичних відхиленнях, коефіцієнт еластичності — в процентах. У табл. 5.2 наведено бета-коефіцієнти останнього (шостого) варіанта моделі врожайності рису. Згідно із значеннями найвагоміший вплив на врожайність рису мають: прополювання (β₆ = 0,360), підживлення (β_4 = 0,264), внесення добрив під основний обробіток (β_{2 =} 0,248).

Для оцінювання адекватності регресійної моделі використовують:

• стандартне відхилення;

• множинні коефіцієнти детермінації та кореляції;

• частинні коефіцієнти детермінації та кореляції;

• коефіцієнти окремої детермінації;

• критерії перевірки істотності зв’язку.

Стандартне відхилення характеризує варіацію залишкових величин

,

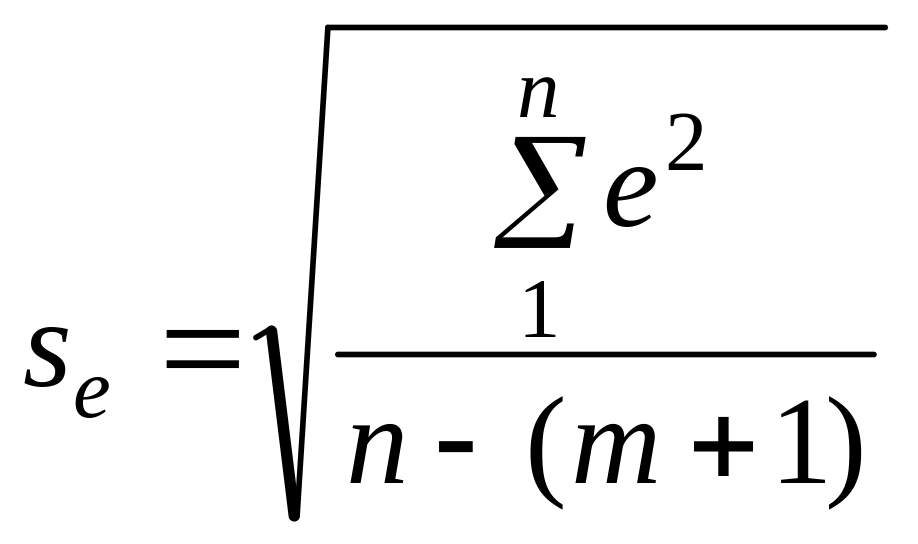де n — обсяг сукупності, m — кількість коефіцієнтів регресії.

Розрахунок характеристик щільності зв’язку ґрунтується на декомпозиції (розкладанні) варіації у за джерелами формування:

,

де — загальна сума квадратів відхилень, зумовлена впливом усіх можливих факторів;

— факторна сума квадратів відхилень, зумовлена впливом включених у модель факторних ознак х_і;

— залишкова сума квадратів відхилень, розмір якої залежить від потужності впливу не включених у модель факторів.

Відношення факторної суми квадратів до загальної характеризує частку варіації у, пов’язану з варіацією включених у модель факторів, і називається множинним коефіцієнтом детермінації

.

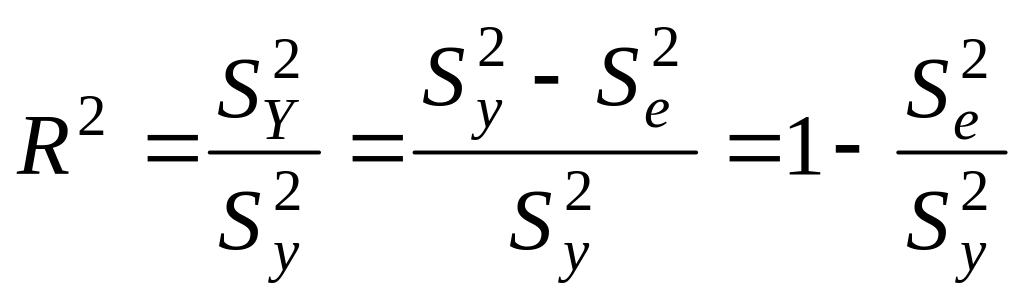За відсутності зв’язку R² ₌ 0. Якщо зв’язок функціональний, то R² ₌ 1. Очевидно, що R² пов’язаний із стандартним відхиленням s_e. При зменшенні s_e значення R² зростатиме і навпаки. Корінь квадратний із коефіцієнта детермінації називають коефіцієнтом кореляції . Для моделі врожайності рису R ₌ 0,8394, R² ₌ 0,7029, тобто 70,29% варіації врожайності рису лінійно пов’язані з агротехнічними факторами, включеними в модель.

Окрім названих множинних коефіцієнтів щільності зв’язку, в комп’ютерних програмах передбачено розрахунок R² з урахуванням числа ступенів вільності:

,

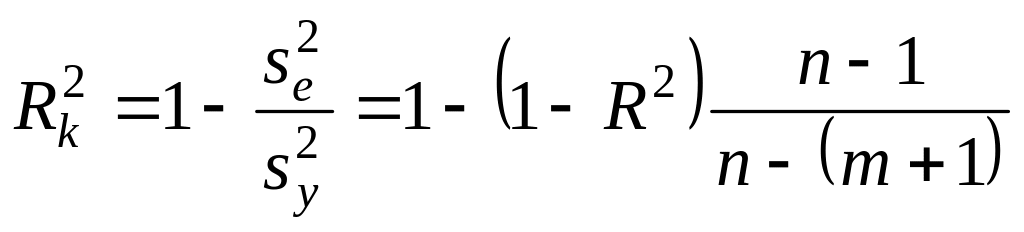де — оцінка дисперсії результативної ознаки у;

— оцінка залишкової дисперсії.

Скоригований коефіцієнт множинної детермінації відрізняється від R² співвідношенням числа ступенів вільності дисперсій: залишкової (n – m + 1) і загальної (n – 1). Для розглянутої моделі це співвідношення становить (34 – 1) : (34 – 6 – 1) _{= =} 1,2222, а ₌ 1 – (1 – 0,7029) ∙ 1,2222 ₌ 0,6369.

У моделях множинної регресії поряд з оцінкою сукупного впливу всіх включених у модель факторів вимірюється кореляція між функцією у та кожним окремим фактором х_і при елімінуванні впливу інших факторів. Для цього використовують частинні кое­фіцієнти детермінації . Схему розрахунку розглянемо на прикладі фактора х₆ моделі врожайності рису. До введення його в модель п’ять факторів пояснювали 64,61% варіації врожайності (R² ₌ 0,6461), не поясненими залишалися (1 – 0,6461) ∙ 100 ₌ 35,39% варіації. Фактор х₆ додатково пояснив 0,7029 –– 0,6461 ₌ 0,0568 варіації у, що відноcно не поясненої іншими факторами варіації становить 0,0568 : 0,3539 ₌ 0,1605. Це і є частинним коефіцієнтом детермінації фактора х₆.

Отже, розрахунок ґрунтується на порівнянні двох регресійних моделей: повної, з урахуванням фактора х_і, і скороченої, у якій фактор х_і відсутній. Чисельник дорівнює різниці сукупних коефіцієнтів детермінації цих моделей, знаменник — одиниці мінус сукупний коефіцієнт детермінації скороченої моделі. Загальну схему його розрахунку можна представити як відношення сум квадратів: частинної і залишкової :

,

де ;

с_іі — діагональний елемент оберненої матриці.

Корінь квадратний із частинного коефіцієнта детермінації називають частинним коефіцієнтом кореляції.

Іноді для характеристики ролі кожного фактора у відтворенні варіації у сукупний коефіцієнт детермінації розкладають на складові:

,

де — коефіцієнт окремої детермінації, який залежить від потужності впливу і-го фактора на у та щільності зв’язку між ними (r_i0 — парний коефіцієнт кореляції).

Ефекти впливу факторів на врожайність рису та характеристики щільності зв’язку наведенo в табл. 5.3.

Таблиця 5.3

Фактор	ri0	bi	βi
x1	0,597	0,965	0,192	0,1146	0,0727
x2	0,614	3,400	0,248	0,1521	0,1160
x3	0,489	0,501	0,045	0,0221	0,0039
x4	0,638	7,500	0,264	0,1687	0,1168
x5	0,411	1,730	0,029	0,0119	0,0020
x6	0,716	3,443	0,362	0,2335	0,1605

У таблиці для кожного фактора наведено три характеристики щільності зв’язку: парний коефіцієнт r_i0, частинний і коефіцієнт окремої детермінації . Найбільші значення мають парні коефіцієнти кореляції. Це пояснюється тим, що фактори взаємозалежні, і парний коефіцієнт кореляції акумулює вплив інших факторів. Частинні коефіцієнти характеризують відносну зміну залишкової дисперсії за рахунок відповідного фактора; для кожного з них база порівняння інша, а тому аналітичні можливості їх обмежені. Коефіцієнти окремої детермінації, сума яких дорівнює множинному коефіцієнту детермінації R² ₌ 0,7029, упорядковуючи фактори за потужністю впливу, практично дублюють висновки, які можна зробити на основі бета-коефіцієнтів.

Перевірка істотності зв’язку статистично формулюється як перевірка нульових гіпотез: H₀ : R² ₌ 0; H₀ : b_i = 0. Гіпотеза Н₀ відхиляється чи визнається допустимою на основі статистичних критеріїв, зокрема дисперсійного F-критерію, статистична характеристика якого розраховується відношенням оцінок факторної і залишкової дисперсій:

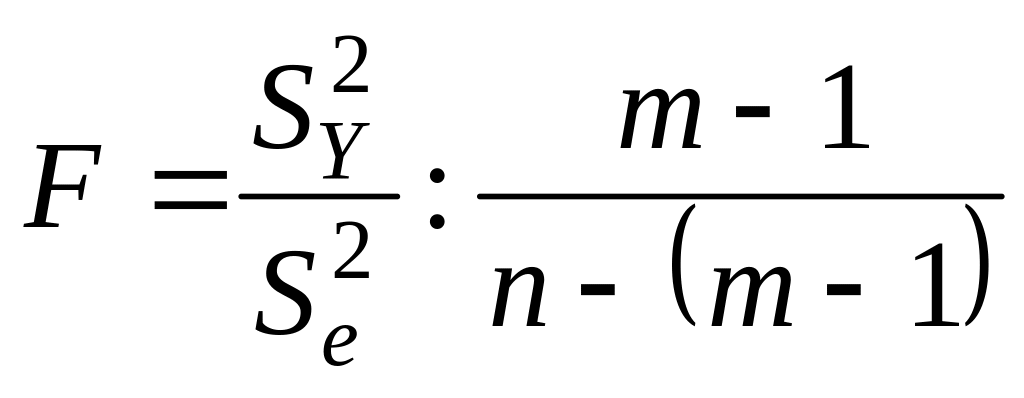або .

Критичні значення , де α — рівень істотності, k_{1 = =} m – 1, k_2 = n – (m – 1) — числа ступенів вільності чисельника та знаменника, наведено в додатку 10. Оскільки F-критерій функціонально зв’язаний з коефіцієнтом детермінації R², то перевірку істотності зв’язку можна здійснити, використовуючи безпосередньо критичні значення , наведені в додатку 11.

Паралельно з оцінюванням адекватності моделі проводиться перевірка істотності впливу окремих факторів х_і на у за допомогою t-критерію:

,

де — стандартна похибка коефіцієнта регресії;

— оцінка залишкової дисперсії;

— діагональний елемент оберненої матриці С.

Критичні значення , де k ₌ n – 1 наведено в додатку 5. Ефект впливу і-го фактора визнається істотним, якщо . Так, при α ₌ 0,05 і k ₌ 20 коефіцієнт b_і в 2,15 раза перевищує стандартну похибку , що свідчить про його значущість (істотність).

Довірчі межі ефекту впливу визначаються за правилами вибіркового методу , де — значення двостороннього t-критерію.

Процедури регресійного аналізу об’єднано в модулі Multiplе Regression — Множинна регресія. Як приклад розглянемо модель залежності виходу цукру з 1 т сировини в кг (y) від цукристості буряка (х₁), втрат сировини при транспортуванні та зберіганні (х₂) та втрат цукру при переробці сировини (х₃). Первинні дані наведено в табл. 2.1.

На стартовій панелі модуля відкриваємо файл даних і проводимо селекцію ознак на залежну (Dependent var.) та незалежні (Independent Variable list). За командою на виконання програми з’являється вікно результатів аналізу — Multiple Regression Results. У верхній, інформаційній частині цього вікна вказується назва залежної ознаки та обсяг сукупності; наводяться значення коефіцієнтів щільності зв’язку: множинної кореляції R, множинної детермінації R² та (у таблицях відповідно R1 та Adjusted R1), значення F-критерію, стандартної похибки — St.errou, вільного члена рівняння регресії b₀ — Intercеpt та його похибки, значення β_i-коефіцієнтів.

У нижній, функціональній частині вікна пропонуються опції, за допомогою яких можна провести всебічний аналіз результатів регресійного аналізу. Так, опція Regression Summary видає таблицю, в якій, окрім зазначених характеристик, наведено для всіх включених у модель факторів β_i-коефіцієнти і коефіцієнти регресії b_і із стандартними похибками, значення t-критерію і фактичні рівні істотності p-level. У табл. 5.4 наведено характеристики регресійної моделі виходу цукру з 1 т сировини.

Таблиця 5.4

Regression Summary for Dependent Variable: VAR4 (new.sta)
Continuе…	R = ,919228 RІ = ,844981 Adjusted RІ = ,802703
	F(3,11)=19,986 p<,00009 Std.Error of estimate: ,36406
N = 15	BETA	St. Err. of BETA	B	St. Err. of B	t(11)	p-level
Intercpt			9,812	8,287	1,184	0,261
VAR1	0,332	0,146	0,953	0,420	2,267	0,044
VAR2	–0,507	0,157	–10,084	3,128	–3,223	0,008
VAR3	–0,377	0,130	–1,729	0,598	–2,888	0,014

Згідно з даними таблиці рівняння регресії має такий вигляд:

Y = 9,812 + 0,953x₁ – 10,084x₂ – 1,729x₃.

Із збільшенням цукристості буряка на 1%, за умови незмінності інших факторів, вихід цукру з 1 т сировини зростає в середньому на 0,953%; щодо порушень технології зберігання та переробки сировини, то вони мають негативний вплив, особливо порушення технології зберігання. Включені в модель фактори пояснюють 84,5% варіації виходу цукру з 1 т сировини; ефекти впливу усіх факторів істотні.

Опція Analysis of variance пропонує таблицю декомпозиції варіації показника-функції, де вказані суми квадратів Sums of Squares: факторна Regress., залишкова Residual та загальна Total, число ступенів вільності df, оцінки дисперсій Mean Squares, значення F-критерію та p-level (табл. 5.5).

Таблиця 5.5

Analysis of Variance; DV: VAR4 (new.sta)
Continuе…	Sums of Squares	df	Mean Squares	F	p-level
Regress.	7,947	3	2,649	19,986	9,27E-05
Residual	1,458	11	0,132
Total	9,405

За опцією Partial cоrrelаtion визначаються частинні коефіцієнти кореляції Partial Cor. для кожної змінної. У таблиці результатів (табл. 5.6), окрім коефіцієнтів частинної і напівчастинної (Semipart Cor.) кореляції, пропонується тест толерантності, за яким оцінюється ступінь зв’язку х_і з іншими включеними в модель факторами. Якщо х_і є лінійною комбінацією інших факторів, то R-square наближується до 1, а Tolerаnce (1 – R²) — до 0. Фактор з малою толерантністю не несе додаткової інформації, і включення його в модель не виправдане.

Таблиця 5.6

Variables currently in the Equation; DV: VAR4 (new.sta)
Соntinue…	Beta in	Partial Cor.	Semipart Cor.	Tolerance	R-square	t(11)	p-level
VAR1	0,332	0,564	0,269	0,656	0,344	2,267	0,045
VAR2	–0,507	–0,697	–0,383	0,570	0,430	–3,223	0,008
VAR3	–0,377	–0,657	–0,343	0,826	0,174	–2,889	0,015