
Основы математического анализа
Если функция f имеет в точке x производную, то существует предел:
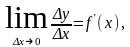 где
где
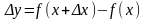 .
.
Отсюда следует, что
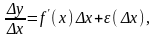 где
где
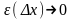 при
при
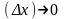
Таким
образом,
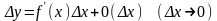 (1)
(1)
Если
ввести обозначение
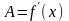 ,
то равенство (1) можно записать следующим
образом:
,
то равенство (1) можно записать следующим
образом:
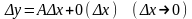 (2)
(2)
говорят,
что функция f
дифференцируема в точке если ее приращение
Dy
в этой точке можно записать в виде (2),
где А –
некоторая константа, не зависящая от
Dx,
но вообще говоря зависящая от x.
Если функция
 имеет в точке x
производную, то она дифференцируема в
этой точке (
).
Верно и обратное утверждение: если
функция дифференцируема в точке x,
т. е. ее приращение в точке x
представимо в виде (2), то она имеет
производную в точке x
равную А.
имеет в точке x
производную, то она дифференцируема в
этой точке (
).
Верно и обратное утверждение: если
функция дифференцируема в точке x,
т. е. ее приращение в точке x
представимо в виде (2), то она имеет
производную в точке x
равную А.
Если
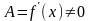 ,
то приращение функции эквивалентно при
,
то приращение функции эквивалентно при
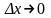 первому
слагаемому правой части (2)
первому
слагаемому правой части (2)
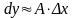 (
).
В этом случае, когда
(
).
В этом случае, когда
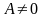 ,
член
,
член
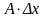 называют
главным линейным членом приращения.
Приближенно, пренебрегая бесконечно
малой
называют
главным линейным членом приращения.
Приближенно, пренебрегая бесконечно
малой
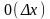 высшего порядка, при малых
высшего порядка, при малых
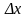 можно считать
можно считать
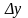 равным главному члену.
равным главному члену.
Главный
линейный член приращения называют
дифференциалом функции
в точке
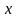 (соответствующим приращению
независимой переменной
)
и обозначают так:
(соответствующим приращению
независимой переменной
)
и обозначают так:
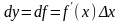 .
.
Приращение
независимой переменной обозначают
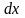 (
(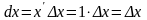 для дифференциала функции
для дифференциала функции
 от
),
таким образом дифференциал функции
в точке
записывается так
от
),
таким образом дифференциал функции
в точке
записывается так
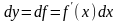 .
.
Отметим очевидные формулы:
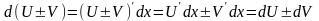
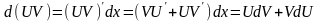
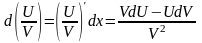 .
.
Производная функции от функции
Пусть
задана функция от функции
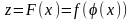 ,
где
,
где
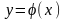 ,
,
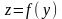 .
При этом функция
.
При этом функция
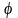 имеет производную в точке
,
а функция
имеет производную в точке
имеет производную в точке
,
а функция
имеет производную в точке
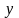 .
Тогда существует производная от
.
Тогда существует производная от
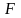 в точке
,
равная:
в точке
,
равная:
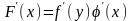 .
.
Таблица производных простейших элементарных функций.
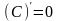
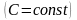
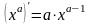 ,
а
– любое число
,
а
– любое число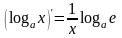 ,
в частности
,
в частности
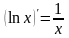
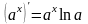 ,
в частности, при
,
в частности, при
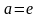 :
:
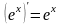
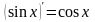
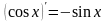
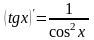
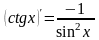
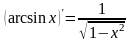
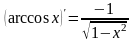
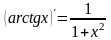
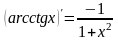
Производные и дифференциалы высшего порядка
Производная
от функции
есть снова функция. Поэтому можно
попытаться взять от нее производную.
Полученная функция (если она существует,
то называется второй производной от
 и обозначается через
и обозначается через
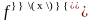 .
Таким образом,
.
Таким образом,
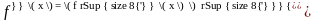 .
.
По
индукции, производная
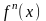 порядка n
определяется как первая производная
от производной
порядка n
определяется как первая производная
от производной
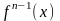 порядка (n
– 1):
порядка (n
– 1):
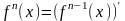 .
.
Дифференциал
от функции
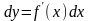 мы будем называть первым дифференциалом
от
в точке
,
соответствующим дифференциалу
(приращению) независимой переменной
мы будем называть первым дифференциалом
от
в точке
,
соответствующим дифференциалу
(приращению) независимой переменной
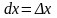 .
.
Дифферециал n-го порядка от функции в точке , соответствующий дифференциалу независимой переменной определяется по индукции:
 .
.
Из
этого равенства следует, что n-я
производная от
в точке
,
есть отношение
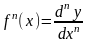 .
.
Первообразная. Неопределенный интеграл
Пусть на интервале (а, b) задана непрерывная функция . По определению функция называется первообразной функцией для на интервале (а, b), если на нем производная от равна :
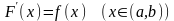
Очевидно,
что если функция
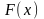 - первообразная для
на (а,b),
а С –
некоторая постоянная, то функция
- первообразная для
на (а,b),
а С –
некоторая постоянная, то функция
 есть также первообразная для
,
потому, что
есть также первообразная для
,
потому, что
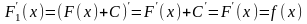
Если
какая-либо первообразная от
на интервале (а,
b),
то возможные первообразные от
на этом интервале выражаются формулой
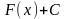 ,
где вместо С
можно подставить любое число.
,
где вместо С
можно подставить любое число.
Неопределенным интегралом от непрерывной функции на интервале (а, b) называется произвольная ее первообразная функция. Неопределенный интеграл обозначается так:
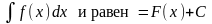 .
.
Если
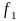 ,
,
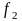 – непрерывные на интервале (а,
b)
функции и
– непрерывные на интервале (а,
b)
функции и
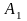 ,
и
,
и
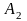 – постоянные, то имеет место следующее
равенство, выражающее основное свойство
неопределенного интеграла:
– постоянные, то имеет место следующее
равенство, выражающее основное свойство
неопределенного интеграла:
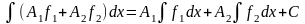 ,
где С
– некоторая постоянная.
,
где С
– некоторая постоянная.
Таблица основных неопределенных интегралов
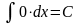 ;
;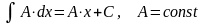 ;
;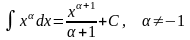 ;
;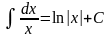 ;
;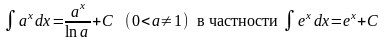 ;
;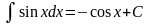 ;
;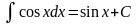 ;
;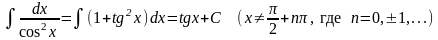 ;
;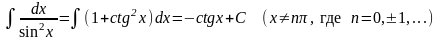 ;
;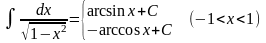 ;
;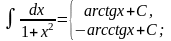
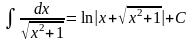 ;
;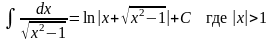 ;
;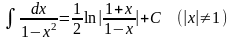 .
.
Понятие определенного интеграла.
