
- •Інститут економіки та нових технологій Кафедра прикладної математики та математичного моделювання
- •Передмова
- •І. Основні питання, що вивчаються в розділі „Функції багатьох змінних ”
- •Поняття функції багатьох змінних.
- •1.3. Послідовності точок в .
- •1.4. Означення функції багатьох змінних.
- •9.2. Найбільше та найменше значення функції в замкненій області. Іі. Основні теоретичні відомості. Приклади розв’язання задач
- •1. Поняття функції багатьох змінних
- •1.1. Евклідовий простір ( )
- •1.2. Множини точок в ( ).
- •1.3. Послідовності точок в ( )
- •Теорема 1
- •1.4. Означення функції багатьох змінних
- •Приклад 4
- •Розв’язання
- •Приклад 5
- •Розв’язання
- •3. Границя та неперервність функцій багатьох змінних
- •3.1. Границя функцій багатьох змінних
- •2.2. Неперервність функції багатьох змінних
- •Теорема 3
- •Теорема 4
- •3. Частинні похідні функції багатьох змінних
- •Приклади 10-11
- •Розв’язання
- •Розв’язання
- •Приклад 12
- •Розв’язання
- •4. Диференціал функції та його використання
- •Теорема 5
- •Приклад 13
- •Розв’язання
- •Приклад 14
- •Розв’язання
- •5. Диференціювання неявних функцій
- •6. Похідна за напрямом. Градієнт
- •Якщо використати теорему Лагранжа, то неважко показати, що (24)
- •Приклад 15
- •Розв’язання
- •7. Частинні похідні вищих порядків
- •Приклад 16
- •Розв’язання
- •8. Застосування частинних похідних в економічних задачах
- •9. Екстремум функції багатьох змінних
- •9.1. Локальний екстремум функції багатьох змінних
- •Теорема 6
- •Приклади 17-18
- •Розв’язання
- •Розв’язання
- •Має максимум, якщо або
- •Має мінімум, якщо або
- •Не має екстремуму, якщо
- •9.2. Найбільше та найменше значення функції в замкненій області
- •Приклад 21
- •Розв’язання
- •Ііі. Завдання для контрольної роботи. Завдання 1
- •Варіанти завдань:
- •Завдання 2.
- •Варіанти завдань:
- •Іv. Список використаної та рекомендованої літератури
Теорема 6
Нехай
точка
– точка екстремуму диференці-йованої
функції
![]() Тоді частинні похідні
Тоді частинні похідні
![]() в цій точці дорівнюють нулеві.
в цій точці дорівнюють нулеві.
Означення 26. Точки в яких та дорівнюють нулеві називаються стаціонарними (або критичними).
Враховуючи,
що частинні похідні є координатами
градієнта функції Z,
можна сказати, що в
точках екстремуму диференційованої
функції
її градієнт дорівнює нулеві, тобто
![]()
Приклади 17-18
Дослідити на екстремум функції.
17.
![]()
Розв’язання
Знайдемо частинні похідні і прирівняємо їх до нуля:
![]() .
.
Звідки
![]() Оскільки
Оскільки
![]() то в стаціонарній точці
то в стаціонарній точці
![]() буде досягатись мінімум функції, як це
видно із рис. 5.
буде досягатись мінімум функції, як це
видно із рис. 5.
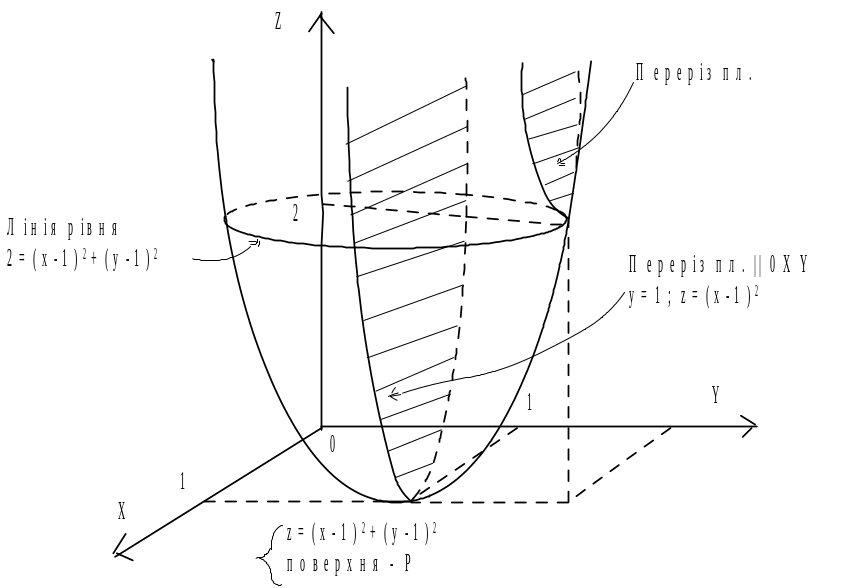
Рис. 5
18.
![]()
Розв’язання
Із
необхідних умов екстремуму
![]() знайдемо критичну точку
знайдемо критичну точку
![]() .
Але критична точка не є ні точкою
максимуму ні точкою мінімуму, тому що
в точці
.
Але критична точка не є ні точкою
максимуму ні точкою мінімуму, тому що
в точці
![]() функція
функція
![]() набуває вигляду
набуває вигляду
![]() а при
а при
![]() і в околі точки
поверхня сильно відрізняється за своїм
виглядом від “шапочки”
та перевернутої “шапочки”.
У критичній точці
ніякого екстремуму немає, ця точка
називається
сідловою,
а поверхня функції
–
сідловою
поверхнею.
Такі сідлові точки є двовимірними
аналогами точок перегину функції однієї
змінної і для того, щоб відділити їх від
точок екстремуму теж потрібні достатні
умови екстремуму. Достатні
умови
екстремуму функцій двох змінних
сформулюємо в термінах других частинних
похідних.
і в околі точки
поверхня сильно відрізняється за своїм
виглядом від “шапочки”
та перевернутої “шапочки”.
У критичній точці
ніякого екстремуму немає, ця точка
називається
сідловою,
а поверхня функції
–
сідловою
поверхнею.
Такі сідлові точки є двовимірними
аналогами точок перегину функції однієї
змінної і для того, щоб відділити їх від
точок екстремуму теж потрібні достатні
умови екстремуму. Достатні
умови
екстремуму функцій двох змінних
сформулюємо в термінах других частинних
похідних.
Теорема 7
(достатні умови екстремуму функцій двох змінних)
Нехай
в околі критичної точки
![]() функція
має
неперервні частинні похідні до другого
порядку включно,
функція
має
неперервні частинні похідні до другого
порядку включно,
![]() .
.
тоді:
Має максимум, якщо або
Має мінімум, якщо або
Не має екстремуму, якщо
Якщо
![]() тоді екстремум в точці
тоді екстремум в точці
![]() може існувати, а може і не існувати і
для його визначення потрібно використовувати
іншу ознаку.
може існувати, а може і не існувати і
для його визначення потрібно використовувати
іншу ознаку.
Приклади 19-20
Дослідити на екстремум такі функції.
19. .
Розв’язання
Знайдемо
критичні точки, обчисливши частинні
похідні
![]()
![]() Критична точка
Критична точка
![]() .
Запишемо достатні умови екстремуму:
.
Запишемо достатні умови екстремуму:
![]() Тоді
Тоді
![]() .
Таким чином функція
екстремуму в точці (0,0) не має.
.
Таким чином функція
екстремуму в точці (0,0) не має.
20.
![]() .
.
Розв’язання
Спочатку знайдемо критичну точку із системи:
![]() =>
=>
![]() =>
=>
![]()
Тоді
![]() .
Запишемо достатні умови екстремуму:
.
Запишемо достатні умови екстремуму:
![]() .
.
Таким
чином у точці
![]() функція
має мінімум.
функція
має мінімум.
9.2. Найбільше та найменше значення функції в замкненій області
Теорема
8.
Якщо
функція
![]() неперервна в замкненій області
,
то вона приймає свої найбільше та
найменше значення в точках області
.
неперервна в замкненій області
,
то вона приймає свої найбільше та
найменше значення в точках області
.
Згідно цієї теореми потрібно знайти точки екстремуму функції , що лежить всередині , екстремальні значення функції в цих точках, значення функції на границі і вибрати серед них відповідно найбільше та найменше значення.
Приклад 21
Знайти
найбільше та найменше значення функції
![]() в області обмеженій лініями
в області обмеженій лініями
![]() ,
що являє собою чотирикутник.
,
що являє собою чотирикутник.
Розв’язання
Знайдемо критичні точки всередині області, записавши необхідні умови екстремуму:
![]()
![]()
![]()
Таким
чином, критична точка
![]() В ній
В ній
![]()
Дослідимо тепер функцію на екстремум на границі чотирикутника:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() Відмітимо, що у випадках а), б), в), г)
вершини чотирикутника враховуються
лише один раз.
Відмітимо, що у випадках а), б), в), г)
вершини чотирикутника враховуються
лише один раз.
а)
У цьому випадку Z буде функцією однієї
змінної y, тому маємо
![]() Дослідимо цю функцію на екстремум на
замкненому відрізку
Дослідимо цю функцію на екстремум на
замкненому відрізку
![]() Знайдемо
Знайдемо
![]() ,
звідки
,
звідки
![]() ,
,
![]() Отже,
Отже,
![]() і в ній
і в ній
![]() Знайдемо значення функції на кінцях
проміжку тобто в точках
Знайдемо значення функції на кінцях
проміжку тобто в точках
![]() та
та
![]() ,
,
![]()
![]()
б)
Аналогічно попередньому досліджуємо
на екстремум функцію
![]() на проміжку
на проміжку
![]() Тому
Тому
![]() ,
,
![]() і критична точка
і критична точка
![]() нe належить проміжку
нe належить проміжку
![]() ,
тобто
,
тобто
![]() В кінці проміжку в точці
В кінці проміжку в точці
![]() знайдемо
знайдемо
![]()
в)
Аналогічно випадку б)
![]() ,
,
![]() і тому
і тому
![]() ,
,
![]() Точка
Точка
![]() ,
на кінці проміжку в точці
,
на кінці проміжку в точці
![]() маємо
маємо
![]()
г)
У цьому випадку
![]() і тому маємо
і тому маємо
![]()
![]()
![]() .
Критична точка
.
Критична точка
![]() Отже
Отже
![]()
Виберемо
тепер серед точок
![]() ті, в яких функція приймає найбільше
та найменше значення. Це будуть точки
ті, в яких функція приймає найбільше
та найменше значення. Це будуть точки
![]() та
та
![]() ,
в яких
,
в яких
![]()
![]()
