6.4. Эффекты локализации и их роль в кэх

Рассмотрим вопрос о физической природе КЭХ, полагая для

определенности, что речь идет об измерениях зависимостей и

, от концентрации электронов при фиксированном магнитном

поле.

Отсутствие и постоянство в некотором интервале

концентраций говорят о том, что во всем этом интервале уровень

химического потенциала остается зафиксированным в промежутке

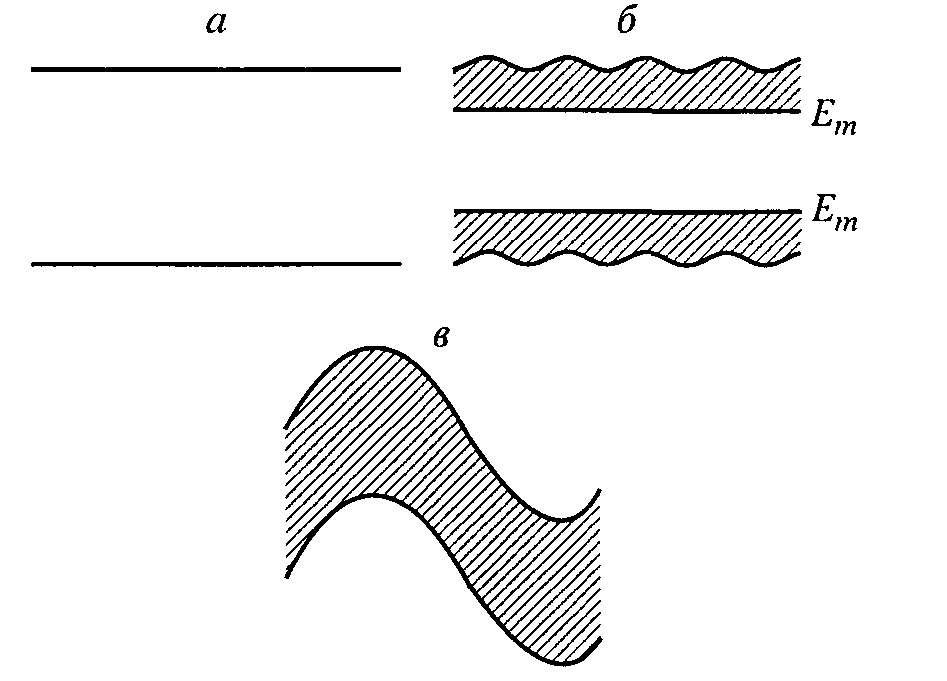
Рис 6.2. Локализация состояний в энергетической зоне с ростом

потенциала неоднородностей. Заштрихована область локализованных со-

состояний.

между уровнями Ландау. Это возможно лишь в том случае, если в

данном промежутке есть какие-то состояния, способные принять

электронов и не изменить при этом ток через образец. Иными

словами, в образце должен существовать резервуар локализованных состояний. Современные физические представления связывают наличие таких состояний с неизбежно существующим в образце случайным потенциалом, вызванным, в частности, флуктуациями в расположении примесных ионов .

Основные понятия о локализации в случайном потенциале бы-

были сформулированы Андерсоном и Моттом около 60 лет тому

назад. Представим себе разрешенную зону энергетических состо-

состояний (рис. 6.2, а). В идеальном кристалле любое состояние в

зоне является делокализованным, т. е. находящиеся в нем электроны

могут свободно двигаться по всему кристаллу. При наличии

случайного потенциала неоднородностей состояния вблизи

края зоны становятся локализованными. Электроны этих состояний двигаются лишь в ограниченной области кристалла, не имея

возможности уйти на большое расстояние, и потому не могут

дать вклада в ток через образец. Вблизи центра зоны располагается

область делокализованных состояний. Уровни энергии ,

разделяющие локализованные и делокализованные состояния, на-

называются порогами подвижности (рис. 6.2, б). Наконец, при

большой амплитуде неоднородностей верхний и нижний пороги

подвижности сливаются и все состояния становятся локализованными

(рис. 6.2, в). Подобный переход в непроводящее состояние

при увеличении амплитуды неоднородностей носит название

перехода Андерсона.

Рис. 6.З. Плотность состояний двумерной системы в перпендикулярном

магнитном поле.

а — идеальный случай; б — при наличии потенциала неоднородностей.

Заштрихована область локализованных состояний.

Изложенные представления можно перенести на случай наличия

магнитного поля и применить для объяснения КЭХ. Идеальная

двумерная система в перпендикулярном магнитном поле

характеризуется чисто дискретным энергетическим спектром (6.1) ,

которому отвечает плотность состояний в виде совокупности

дельта-функций (6.3). Наличие случайного потенциала приводит к

тому, что разные точки пространства становятся неравноправными

и энергия электрона в магнитном поле начинает зависеть от

положения центра электронной орбиты. Это приведет к уширению

пиков плотности состояний и появлению порогов подвижности

(рис. 6.3).

В реальных кристаллах из-за действия рассеяния электрон может находиться на каждом уровне лишь время порядка , соответствующее времени свободного пробега. Как следует из принципа неопределенности «энергия-время» , каждый уровень приобретает ширину ~ . Уже поэтому плотность состояний приобретает вид острых максимумов конечной ширины.

Изложенных представлений достаточно для качественного

объяснения КЭХ. Действительно, в интервале концентраций, когда

уровень Ферми лежит в области локализованных состояний между

пиками g{E) (уровнями Ландау), число заполненных делокализо-

ванных состояний не меняется, а потому не меняется и , ибо в

проводимость дают вклад лишь делокализованные электроны. На

зависимости наблюдается плато.

Приведенные элементарные рассуждения объясняют сам факт

наличия холловских плато, но не значения на плато. Действительно,

если делокализована лишь часть электронов, скажем, равная ( < 1),

то во всех формулах для проводимости следует, на первый взгляд,

заменять на , что приведет к дополнительному множителю в формуле (6.16). Ответ заключается в том, что потенциал неоднородностей, локализуя часть носителей, одновременно меняет и свойства делокализованных электронов. Их скорость холловского дрейфа возрастает, что компенсирует уменьшение их концентрации и приводит к сохранению фундаментальной формулы (6.16).

Рис. 6.4. Измерение эффекта Холла в геометрии диска Корбино.

Сделанное утверждение носит общий характер и не зависит от

вида потенциала неоднородностей и геометрии системы. Чтобы

доказать это, мы приведем более общий вывод формулы (6.9), не

использующий результаты квантово-механических расчетов, упо-

упомянутых в разделе 6.1 и справедливых лишь для свободных элект-

электронов.

Рассмотрим образец с двумерным электронным газом, имеющий

кольцевую геометрию, показанную на рис. 6.4 (диск Корбино) и

содержащий некоторый потенциал неоднородностей. Пусть заполнен один уровень Ландау. Мы будем пользоваться квазиклассическим приближением и описывать электроны двумерным импульсом р. Движение по кольцу — периодическое и потому должно удовлетворять условиям квантования Бора—Зоммерфельда , которые в магнитном поле имеют вид

, (6.11)

где А — вектор-потенциал магнитного поля.

Изменим мысленно магнитное поле в отверстии кольца, не ме-

меняя его в области > , где находятся электроны. При этом

физически наблюдаемые свойства электронов не могут меняться,

поскольку они определяются величиной магнитного поля,

действующего на электроны. Однако будут меняться А и фаза волновой

функции, в которую он входит. Если полное изменение магнитного потока через отверстие будет равно , то фазы всех волновых функций изменятся на и вся электронная картина вернется в исходное состояние. На первый взгляд, ничего не изменилось. Но на самом деле при

изменении А менялась электронная траектория. Увеличение А

уменьшало обобщенный импульс , и при этом для выполнения условия квантования (6.11) должен был возрастать радиус траектории.

Тот факт, что в результате описанной процедуры картина не изменилась, означает, что система уровней приобрела исходный вид, но каждый электрон переместился на соседнюю квантованную траекторию большего радиуса, электрон с последней траектории ушел во внешний контакт при , а один электрон с внутреннего контакта вошел в кольцо. Все это в целом

выглядит как перемещение одного электрона с контакта в

контакт .

Рассмотрим баланс энергии при описанном выше действии.

Поскольку разность потенциалов между указанными контактами

равна холловскому напряжению , при этом совершается работа

. Взглянем на проблему с другой стороны. При изменении

магнитного поля в отверстии всюду, в том числе и в плоскости,

содержащей электроны, возникало индукционное электрическое поле.

Согласно законам электрической индукции, при изменении на

магнитного потока через контур с током I энергия системы

меняется на . В нашем случае и .

Поскольку уровень Ферми лежит в области локализованных

состояний и , то диссипативных токовых потерь индукционное

поле не вызывает. Поэтому из баланса энергии следует, что

, т. е.

. (6.12)

Аналогичные рассуждения для системы с N заполненными

уровнями Ландау дали бы дополнительный множитель N в формуле

(6.12). Высказанные аргументы могут служить доказательством

универсального характера формулы КЭХ (6.9).