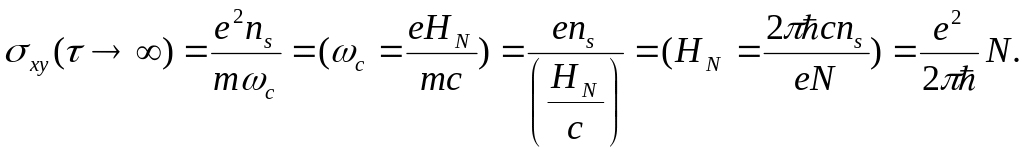Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Квантовый эффект Холла.doc

Скачиваний:

Добавлен:

14.11.2019

Размер:

1.01 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Глава. СИЛЬНЫЕ МАГНИТНЫЕ ПОЛЯ И КВАНТОВЫЙ

ЭФФЕКТ ХОЛЛА

Уравнение Шредингера в магнитном поле. Движение в однородном

магнитном поле.

Хорошо известно, что в случае сильных магнитных полей Н,

удовлетворяющих условию >> и >> ( —

циклотронная частота, — время релаксации), классическое

описание явлений переноса неприменимо и требуется квантово-меха-

нический подход (такие магнитные поля называются квантующими). Это относится и к случаю двумерного электронного газа. Более того, как мы увидим ниже, свойства двумерных систем в квантующих полях еще более разительно, нежели в трехмерном случае, отличаются от предсказаний классической теории.

Как известно, частица со спином обладает и собственным магнитным моментом , причем

, (1)

где - величина спина частицы, а - характерная для частицы постоянная. Собственные значения проекции магнитного момента равны . Отсюда видно, что коэффициент (который называют обычно величиной магнитного момента) представляет собой наибольшее возможное значение , достигаемое при проекции спина . Отношение - дает отношение собственного магнитного момента частицы к ее собственному механическому моменту, когда оба направлены по оси z. Для электрона

= - . Поэтому собственный момент электрона (спин равен

- , где

=0,927 эрг/гаусс.

Эту величину называют магнетоном Бора.

В классической теории гамильтониан заряженной частицы в электромагнитом поле имеет вид

где -скалярный, -векторный потенциал поля, - обобщенный импульс частицы. Если частица не обладает спином, то переход к квантовой механике

производится обычным образом: обобщенный импульс надо заменить оператором , и мы получаем гамильтониан

. (3)

Собственный магнитный момент частицы непосредственно взаимодействует с магнитным полем. Поэтому необходимо добавить в гамильтониан дополнительный член - , соответствующий энергии магнитного момента в магнитном поле. Поэтому гамильтониан частицы, обладающей спином, имеет вид

. (4)

Волновые функции, на которые действует гамильтониан (4), - спиноры. Волновая функция частицы со спином имеет две компоненты: и . Двухкомпонентную величину

называют спинором . Согласно правилу коммутации оператора импульса с любой функцией координат

= . (5)

В классической механике

В квантовой механике

. (6)

Для операторов компонент скорости имеют правила коммутации

. (7)

которые проверяются непосредственным вычислением. В силу (7) частица не может иметь одновременно определенных значений скорости по всем трем направлениям.

Определим уровни энергии частицы в постоянном однородном магнитном поле.

Выберем векторный потенциал однородного поля в форме:

. (8)

Ось z выбрана в направлении магнитного поля. В самом деле имели

= .

Тогда гамильтониан принимает вид

. (9)

Оператор коммутирует с гамильтонианом, поскольку последний не содержит операторов других компонент спина. Это значит, что z-проекция спина сохраняется и поэтому можно заменить собственным значением . После этого спиновая зависимость волновой функции становится несущественной и в уравнении Шредингера можно понимать как обычную координатную функцию. Для этой функции имеем уравнение

. (10)

Гамильтониан этого уравнения не содержит явно координат и , поэтому с ним коммутативны операторы обобщенного импульса и , то есть величины и сохраняются. Поэтому ищем в виде

. (11)

Поскольку , то z-компонента обобщенного импульса совпадает с z-компонентой обычного импульса . Величины и пробегают все значения от до . Таким образом, скорость частицы в направлении поля может иметь произвольное значение. Движение вдоль поля «не квантуется».

Далее (11) подставляется в (10). После чего получим

. (12)

Введем обозначения

. (13)

С учетом данных обозначений перепишем (12) в виде

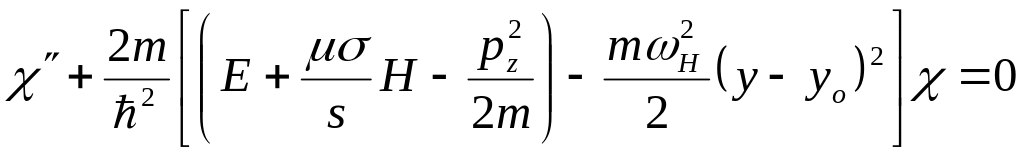. (14)

Уравнение (14) по форме совпадает с уравнением Шредингера для линейного осциллятора, колеблющегося с частотой

(15)

Поэтому мы можем сразу заключить, что выражение в круглых скобках в (14) может принимать значения , где .

Таким образом, получаем следующее выражение для уровней энергии частицы в однородном магнитном поле

(16)

Первый член в (16) дает дискретные значения энергии, отвечающие движению в плоскости, перпендикулярной к полю (уровни Ландау). Так как для электрона , то формула (16) принимает вид

(17)

При этом

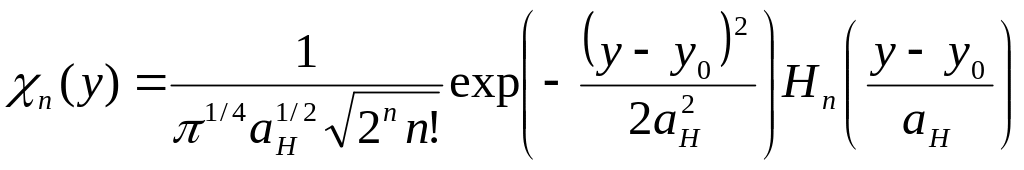, (18)

где .

В классической механике движение частиц в плоскости, перпендикулярной к магнитному полю (плоскость xy) , происходит по окружности с неподвижным центром. Сохраняющаяся в квантовом случае величина соответствует классической y-координате центра окружности. Наряду с ней сохраняется также величина

так как ее оператор коммутативен с гамильтонианом. Эта величина соответствует классической x- координате центра окружности. Однако операторы и не коммутативны друг с другом, так что координаты и

не могут одновременно иметь определенных значений.

Поскольку (16), (17) не содержат величины , пробегающей непрерывный ряд значений, уровни энергии вырождены с непрерывной кратностью. Кратность вырождения, однако, становится конечной, если движение в плоскости xy ограничено большой, но конечной площадью . Число различных (теперь дискретных) значений в интервале равно

Допустимы все значения , для которых центр орбиты находится внутри . Из условия 0 < < имеем (

, .

Следовательно, число состояний для заданных и есть

. (19)

Если область движения ограничена также и вдоль оси длиной , то число возможных значений в интервале есть и число состояний в этом интервале есть

(20)

Для электрона имеет место еще дополнительное вырождение: уровни энергии совпадают для состояний с квантовыми числами и .

Энергетический спектр и плотность состояний

двумерных систем в магнитном поле

При рассмотрении свойств двумерных систем в квантующих

магнитных полях первое, что необходимо сделать, — это определить энергетический спектр системы путем решения уравнения

Шредингера, что было сделано в предыдущем разделе.

Прежде всего заметим, что в зависимости от ориентации магнитного поля относительно плоскости двумерного слоя могут реализоваться два случая, ответы для которых качественно различны. Если лежит в плоскости слоя, то основным результатом будет увеличение энергий квантово-размерных уровней за счет дополнительного ограничения движения носителей магнитным полем. Это упрощает наблюдение ряда эффектов, так как позволяет легко менять в эксперименте энергии уровней, что во всех структурах, за исключением МДП-транзисторов, в отсутствие магнитного поля является весьма непростой задачей. Происходит также некоторое

увеличение эффективной массы, описывающей свободное движение в плоскости слоя. В целом можно сказать, что параллельное магнитное поле сохраняет качественный характер энергетического спектра и плотности состояний , хотя и меняет количественно его параметры и m. Принципиально новых эффектов здесь не ожидается, и мы не будем далее обсуждать случай параллельного поля.

Ситуация, когда магнитное поле ориентировано по нормали к

слою (вдоль оси z), значительно более интересна. Хорошо

известно, что классические траектории частиц в плоскости,

перпендикулярной магнитному полю, представляют собой окружности. В

квантовой механике такое периодическое вращение отвечает

системе эквидистантных дискретных уровней Ландау:

, N=0, 1, 2, … (6.1)

Формула (6.1) записана без учета спина.

В массивных трехмерных полупроводниках или металлах к

спектру (6.1) добавляется , как мы видели, еще непрерывный квадратичный спектр , связанный с движением вдоль поля, поэтому суммарная

плотность состояний отлична от нуля при любой энергии, превос-

превосходящей . Однако в двумерных системах движение по

оси z квантовано, так что полный спектр представляет собой сумму

(6.1) и энергий квантово-размерных уровней и, таким образом, является

чисто дискретным. Удивительным является то, что чисто дискретный

спектр обычно характерен для микроскопических объектов

(атомы, квантовые точки и др.). Здесь же мы имеем дело с

макроскопической системой.

В дальнейшем мы ограничимся рассмотрением двумерной

системы с одним заполненным квантово-размерным уровнем

(необходимые критерии этого приведены ранее). Если энергию

этого уровня выбрать за начало отсчета, то формула (6.1) будет

описывать полный энергетический спектр системы, а не только

его часть, связанную с движением в плоскости ху.

Энергетический спектр (6.1) является сильно вырожденным,

т. е. каждому уровню Ландау соответствует не одно, а много

электронных состояний. Физически природа вырождения достаточно

понятна: в плоскости ху система однородна, что означает, что

состояния, отличающиеся друг от друга лишь положением центра

электронной орбиты, должны иметь одну и ту же энергию.

Простые расчеты показывают, что кратность вырождения

(число различных состояний с одинаковой энергией) в расчете на

единицу площади двумерной структуры равна, согласно формуле (19) предыдущего раздела

. (6.2)

Дискретному электронному спектру (6.1) соответствует плотность состояний в виде совокупности резких пиков, в идеальном случае дельта-функций:

. (6.3)

В реальных структурах за счет рассеяния носителей и неоднородного потенциала заряженных примесей дельта-функции будут размываться

в пики с конечной шириной и высотой. Более подробно этот вопрос будет обсуждаться в разделе 6.4.

До сих пор мы не учитывали спин электрона. Наличие спина

приводит к тому, что каждый уровень Ландау двукратно

расщепляется на состояния с энергиями , где —

магнетон Бора, a — спиновое гиромагнитное отношение

(эффективный g-фактор для электронов). Эта величина, так же как и,

скажем, эффективная масса носителей , определяется деталями

зонной структуры и может меняться от вещества к веществу во

много раз. Используя известные значения m и для наиболее

распространенных полупроводников, можно показать, что величина

спинового расщепления , как правило, заметно меньше рас-

расстояния между уровнями Ландау. Существует простой и надежный способ экспериментального разделения эффектов орбитального и спинового квантования, основанный на использовании так называемого наклонного

магнитного поля. Если отклонено от нормали к двумерному слою

на угол , то квантование Ландау (орбитальные эффекты)

определяется лишь нормальной компонентой поля , а спиновое

расщепление не зависит от ориентации поля и пропорционально

его полной величине Н.

6.2. Кинетические явления в сильных магнитных полях

Чисто дискретный спектр двумерной электронной системы в

перпендикулярном магнитном поле приводит к существенной

модификации ее гальваномагнитных свойств по сравнению с

трехмерным случаем. Отсутствие третьей степени свободы

(свободного движения вдоль поля) приводит к тому, что вероятность

упругого рассеяния носителей испытывает гигантские осцилляции с

магнитным полем.

Действительно, представим себе, что напряженность магнитного

поля Н в точности равна

(N = 1, 2,...).

Тогда при низких температурах все электронов, находившиеся в двумерном электронном газе на единицу его площади, полностью заполняют N подуровней Ландау — какие-либо свободные места на них

отсутствуют.

В самом деле, при полном заполнении уровня Ландау кратность вырождения (6.2) – это число электронов на нем. Если рассматривается уровней Ландау и все они заполнены, то

Отсюда и получается формула для .

При полном заполнении уровней Ландау в силу принципа Паули электронных переходов внутри уровней нет. При упругом рассеянии невозможны также переходы на свободные состояния вышележащих уровней, так как это требует дополнительной энергии. Поэтому процессы

рассеяния, представляющие собой переходы из одного состояния в

другое под действием рассеивающего потенциала, в указанных

условиях невозможны.

Чтобы понять, к каким следствиям может привести влияние

магнитных полей на процессы рассеяния, рассмотрим кратко

классическую картину проводимости в сильном магнитном поле. Пусть

магнитное поле направлено по оси z, а тянущее электрическое

поле — по оси х. Пусть скорость направленного движения

электрона описывается вектором . Тогда сила, действующая на него со

стороны полей (сила Лоренца), равна . Рассеяние носителей

можно феноменологически рассматривать как эффективную силу тре-

трения, пропорциональную скорости и направленную навстречу ей:

(где — время релаксации) . В постоянных полях

дрейфовая скорость электрона постоянна, следовательно,

сумма действующих на него сил равна нулю:

. (6.4)

Расписывая уравнение (6.4) по компонентам и определяя из него

компоненты скорости и , получаем:

;

Разрешая полученную выше систему алгебраических уравнений относительно и , находим

. (6.5)

Если — концентрация двумерных электронов, то величина

e представляет собой линейную (в расчете на единицу длины)

плотность тока . Поскольку связь между векторами F и j дается

тензором проводимости , то из (6.5) сразу имеем выражения для

диагональной (диссипативной) и недиагональной (холловской)

компонент проводимости:

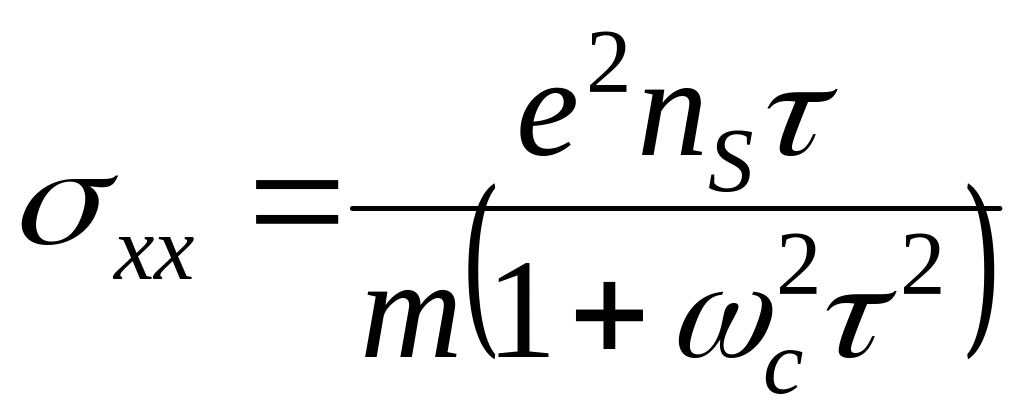, (6.6)

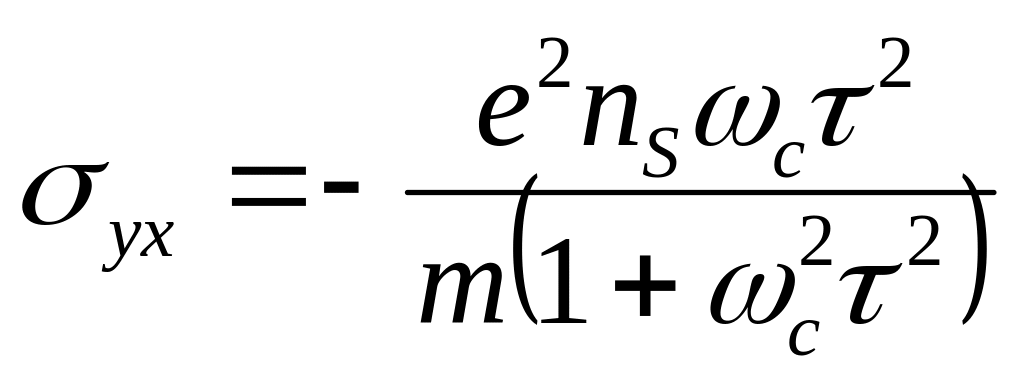. (6.7)

Пусть поле направлено теперь по оси OY. Теперь из (6.4) имеем

, (6.8)

. (6.9)

Теперь находим

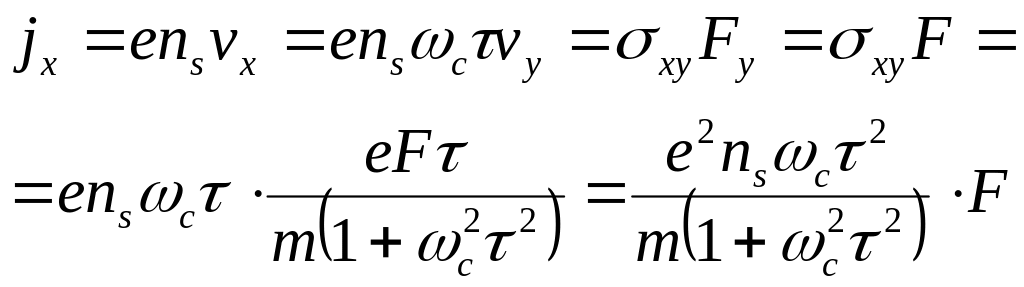Отсюда получается выражение для . Пусть поле направлено по оси OX.

Имеем

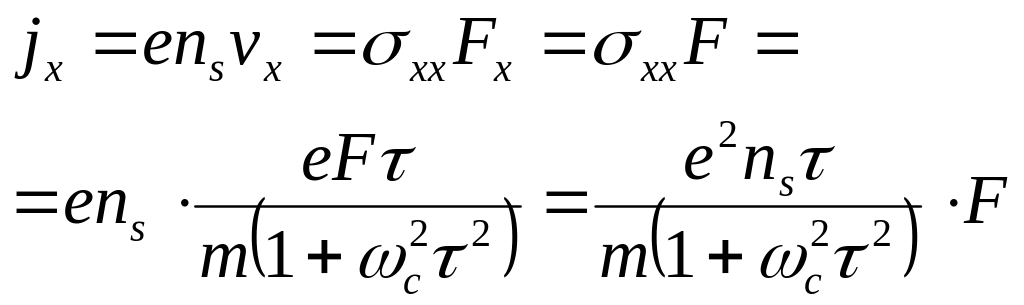
Отсюда вытекает выражение (6.6). Если рассмотреть случай поля , направленного по оси OX, то ,повторяя предыдущие рассуждения, легко найти

Перепишем соотношение ( , по подразумевается суммирование от 1 до 3 ) в матричной форме

. (6.10)

Обозначим через матрицу сопротивления. Имеем

= = = , . (6.11)

Обратная матрица находится по обычным правилам

. (6.12)

Здесь - присоединенная матрица, полученная транспонированием из матрицы, составленной из алгебраических дополнений к элементам . Напомним, что алгебраическое дополнение к элементу произвольной матрицы - определитель, который получается после вычеркивания -той строки и -того столбца , умноженный на . Очевидно, в нашем случае

Далее имеем

. (6.13)

Отсюда находим

, . (6.14)

Из выражений (6.6) и (6.7) видно, что в сильных магнитных полях ( >>1) диссипативная проводимость пропорциональна вероятности рассеяния , а холловская проводимость не зависит от рассеяния.

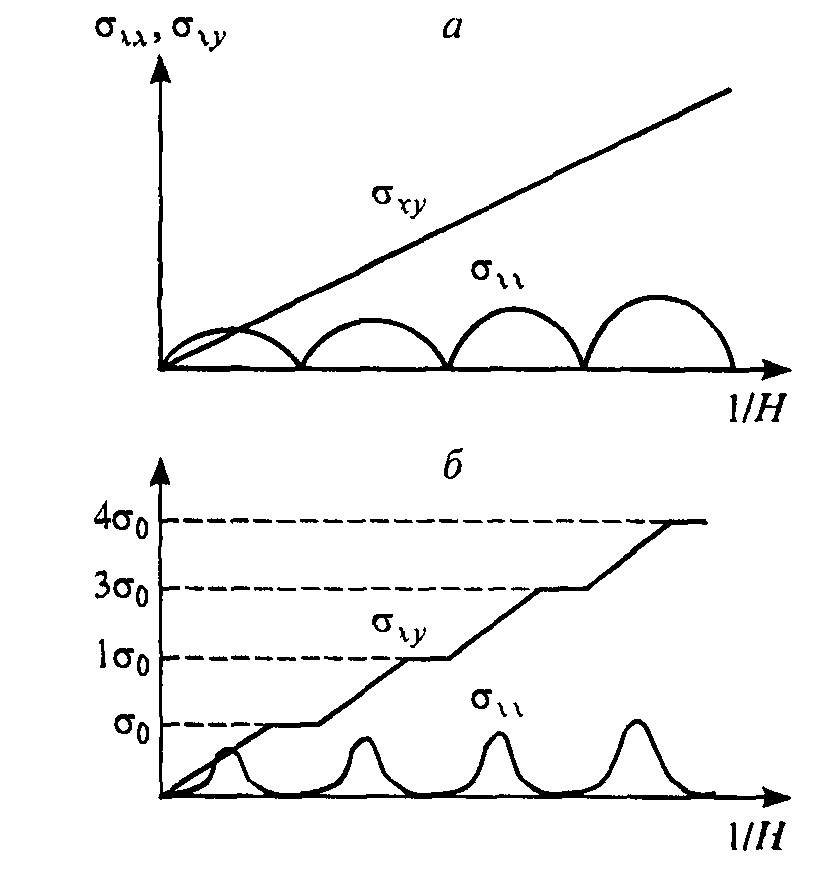
Рис. 6.1. Полевые зависимости и в сильных магнитных полях для

идеального двумерного газа (а) и в реальных экспериментах (б) ( ).

Физически это связано с характером движения

электронов в скрещенных (взаимно перпендикулярных) полях F и Н. Оно представляет собой вращение по круговым орбитам с частотой при одновременном дрейфе центра орбиты со скоростью . При этом среднее смещение электрона вдоль F отсутствует и появляется