Распределение Максвелла

Закон распределения по скоростям молекул газа, находящегося в термодинамическом равновесии, был найден Максвеллом (1859 г.).

Следуя Максвеллу, представим себе пространство скоростей с прямоугольными координатными осями, по которым будем откладывать значения проекций скорости v_x , v_y , v_z отдельных молекул. Тогда скорости каждой молекулы будет соответствовать точка в этом пространстве - конец вектора v. Из-за столкновений молекул положения точек будут стремительно меняться (при нормальных условиях каждая молекула газа испытывает порядка 10⁹ столкновений в секунду), но их распределение в целом будет оставаться неизменным, поскольку макросистема находится в термодинамическом (статистическом) равновесии. Вследствие равноправности всех направлений движения расположение точек относительно начала координат будет сферически симметричным. Поэтому плотность точек может зависеть только от модуля скорости v.

Пусть макросистема (газ) содержит N молекул. Выделим в некоторой точке - конце вектора v - малый объем dv_xdv_ydv_z (рисунок, где ось z направлена на нас). Относительное число точек (молекул) в этом объеме dN / N, или другими словами, вероятность dP того, что скорость молекулы, т.е. конец вектора v, попадет в этот объем, можно записать так:

где f(v) имеет смысл объемной плотности вероятности.

Вероятность же того, что молекула (точка) будет иметь проекции скорости в интервале (v_x , v_x + dv_x), есть

где (v_x) - функция распределения по v_x. Последнее выражение - это по существу интеграл от предыдущего по v_y и v_z , т.е. относительное число молекул в тонком плоском слое от v_x до v_x + dv_x.

Вероятности того, что молекула имеет проекции скорости в интервалах (v_x , v_x + dv_x), (v_у , v_у + dv_у) и (v_z , v_z + dv_z), являются независимыми (это было строго доказано), поэтому в соответствии с теоремой об умножении вероятностей независимых событий можно записать

Из соображения равноправия осей v_x , v_y , v_z ясно, что функции  должны одинаковым образом зависеть от соответствующих проекций скорости.

Объемную плотность вероятности можно выразить через плотности вероятностей для проекций скорости:

f(v) = (v_x)(v_y)(v_z)

Возьмем логарифм от обеих частей последнего выражения:

lnf(v) = ln(v_x) + ln(v_y) + ln(v_z)

Дифференцируем последнее выражение по v_x:

Учитывая, что , для производной можно получить выражение:

.

Подставляем значение производной в уравнение:

Правая, следовательно, и левая части последнего уравнения не зависят от v_y и v_z. Значит, они не зависят от v_x, поскольку v_x, v_y, v_z входят в функцию f(v) симметрично. Следовательно, правую часть уравнения можно приравнять к некоторой неизвестной пока константе, которую обозначим (). Отрицательный знак введен, с учетом дальнейшего, для того, чтобы величина  оказалась положительной. Получим дифференциальное уравнение для функции (v_x):

Разделим переменные (частную производную заменим на полную, поскольку они эквивалентны в данном случае):

В результате интегрирования получаем:

, где А - неизвестная константа интегрирования.

Очевидно, для (v_y) и (v_z) можно получить такие же выражения. Для f(v) получим:

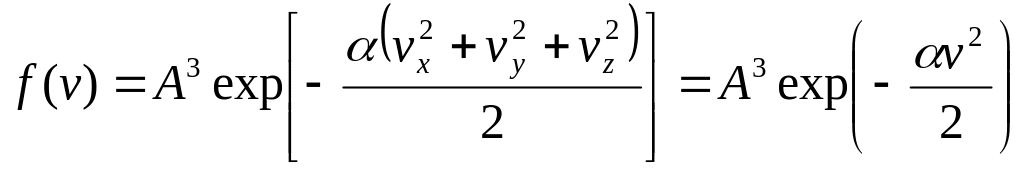
Из последнего выражения следует положительный знак константы , поскольку иначе наблюдался бы неограниченный рост функции f(v).

Константу А можно определить из условия нормировки:

Интеграл в последнем выражении известен в математике под названием интеграла Пуассона, его величина равна . Отсюда: .

Осталось определить величину константы . Это возможно путем использования полученной ранее формулы для среднего значения кинетической энергии поступательного движения молекул:

Поскольку движения молекулы во всех направлениях равноправны, можем записать:

.

Имея полученное выше выражение для функции распределения (v_x), которое содержит неизвестную константу , можно выразить среднее значение , приравнять его к полученному выше значению kT/m и определить таким способом константу :

Известное из математики значение интеграла равно , отсюда .

Окончательные результаты таковы:

График функции (v_x) изображен на рисунке. Он совпадает с гауссовой кривой погрешностей. Площадь тонированной полоски - это вероятность того, что проекция скорости лежит в интервале (v_x , v_x + dv_x). Функция нормирована на единицу, т.е. площадь под кривой (v_x)