11

Статистическая физика Распределение Максвелла и Больцмана Вероятность. Средние значения

Статистическая физика - это раздел физики, в котором изучают свойства макросистем, исходя из индивидуальных свойств составляющих макросистему частиц и взаимодействий между ними. Описание движения каждой частицы макросистемы (а их порядка 10²² - 10²³) - задача совершенно немыслимая. Вместо этого статистическая физика оперирует со средними значениями параметров очень большого числа частиц. Колоссальное число частиц в макросистеме приводит, несмотря на очевидный хаос, к появлению новых, статистических закономерностей. Их изучение и делает возможным описание макросистем на основе сведений о свойствах отдельных частиц.

О вероятности. Основу статистической физики составляет теория вероятностей. исходные понятия этой теории - событие и вероятность.

Событие - это, например, выпадение одного из шести номеров при бросании игрального кубика. Или при измерении скорости молекул газа: разбив возможные значения скоростей на отдельные интервалы v_i (i = 1, 2, ...) и обнаружив, что скорость молекулы попала в i-тый интервал, мы говорим об i -том событии.

В дальнейшем нас будут интересовать лишь такие события, которые являются:

1) случайными, т.е. событиями, условия наступления которых по тем или иным причинам неизвестны и которые поэтому нельзя заранее с уверенностью предсказать;

2) равновозможными или равновероятными - для которых нет никаких оснований ожидать, что при испытаниях они будут вести себя по-разному (например, при бросании игрального кубика или монеты).

Вероятность данного случайного события характеризуется кратностью его повторения. Если в N случаях i-тое событие происходит N_i раз, то вероятностью Р_i этого события называют величину

Так как на практике N всегда конечно, то для вычисления вероятности стараются, чтобы N и N_i были достаточно большими. Тогда можно считать, что

P_i  N_i / N

Сумма вероятностей всех возможных результатов измерений равна единице:

Теорема сложения вероятностей

Если в результате N бросаний кубика в N_i случаях выпадет число i, а в N_k случаях - k, то вероятность выпадения i или k равна

Р(i или k) = = P_i + P_k

Это значит, что при бросании кубика вероятность выпадения, скажем, 2 или 5 равна Р = 1/6 + 1/6 = 1/3.

В общем случае:

вероятность появления в испытаниях одного из нескольких несовместимых событий равна сумме вероятностей каждого из этих событий.

Теорема умножения вероятностей

Найдем вероятность, что при двух бросаниях кубика выпадет последовательно i и k. Рассмотрим N двойных бросаний. Пусть первый из каждой пары бросков дал i в N_i случаях (так что Р_i  N_i / N). Теперь выделим из этих N_i случаев те N_k событий, когда второй бросок кубика давал k (так что Р_k  N_k / N_i). Тогда искомая вероятность

Р(i, затем k) =

Значит, вероятность того, что при бросаниях кубика выпадут, допустим, сначала 2, а затем 5, равна 1/6  1/6 = 1/36

В общем случае теорема умножения вероятностей утверждает:

вероятность совмещения двух или нескольких независимых событий равна произведению вероятностей каждого из них в отдельности.

Средние значения случайных величин

Случайная величина, которая может принимать ряд дискретных значений, для каждого из которых имеется своя вероятность, называется дискретной случайной величиной. Например, число молекул газа, залетевших в некоторый объем в данный момент времени – дискретная случайная величина. Она может принимать значения в виде последовательности целых чисел. Зная вероятности появления различных результатов измерений дискретной случайной величины х, можно найти их среднее значение х . По определению среднего

х=

Функция распределения

Рассмотрим случай, когда случайная величина х имеет непрерывный характер (например, скорости молекул). Для этого разобьем всю область изменения х на отдельные интервалы и будем считать число попаданий случайной величины в тот или иной интервал. Интервалы должны быть во избежание заметных флуктуаций достаточно большими, чтобы в каждом интервале число попаданий было N_i  1 и можно было бы по частоте попадания достаточно точно определить вероятность попадания случайной величины в данный интервал. Вместе с тем, интервалы должны быть достаточно небольшими, чтобы более детально характеризовать распределение величины х.

Итак, мы имеем достаточно большое число достаточно небольших интервалов и, допустим, нам известна вероятность Р_х попадания в тот или иной интервал х. Сама величина Р_х весьма мала. Поэтому в качестве характеристики случайной величины берут отношение Р_х / х , которое для достаточно малых х не зависит от величины самого интервала х.

Это отношение при х  0 называют функцией распределения f(x). Этой функции можно приписать смысл плотности вероятности, т.е. вероятности интересующей нас величины оказаться в единичном интервале вблизи значения х.

В разных случаях функция распределения имеет совершенно различный вид, один из которых в качестве примера приведен на рисунке.

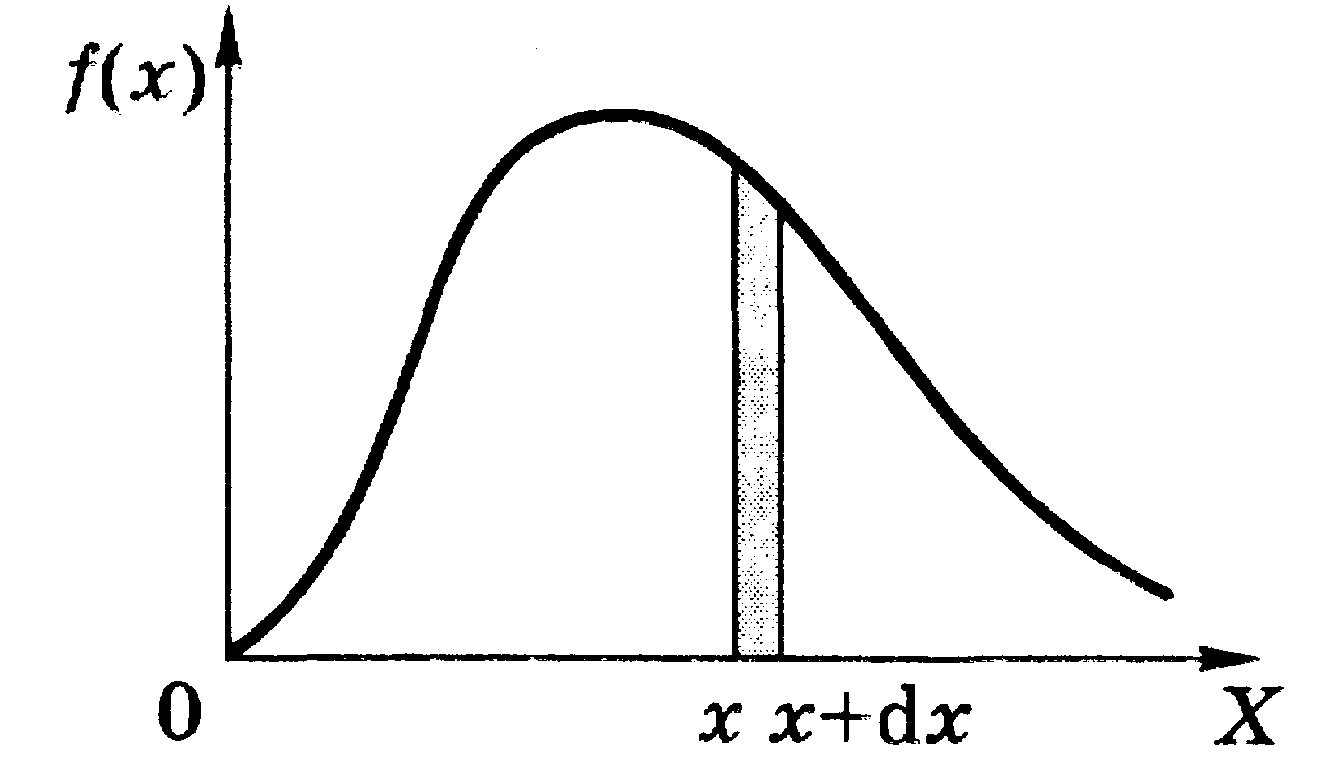
Площадь полоски шириной dx на этом рисунке равна вероятности того, что случайная величина х окажется в пределах интервала (х, х + dx):

dP_x = f(x) dx

Вероятность того, что величина х попадает в интервал (а, b) (согласно теореме о сложении вероятностей):

Вероятность того, что величина х может принять какое-либо значение (достоверное событие), равна единице. Это называют условием нормировки:

,

где интегрирование производится по всему интервалу возможных значений величины х. Из этого условия следует, что вся площадь под кривой f(x) равна единице.

Средние значения

Среднее значение величины х можно найти, зная ее нормированную на единицу функцию распределения f(x). Обратимся к формуле для среднего значения дискретной величины:

х =

Формула справедлива и для случая, когда интервал изменения величины х будет разбит на небольшие участки. Уменьшая участки, мы должны в конце концов заменить Р_i на dP и сумму на интеграл:

х = ,

где интегрирование проводится по интересующему нас интервалу значений х. Аналогичные формулы справедливы для любой функции (х), например

х² = .

Флуктуации

Вероятность случайного события и экспериментально наблюдаемая доля результатов, когда событие осуществляется, - это не одно и то же. Последняя (доля результатов) испытывает случайные отклонения от предсказываемой вероятности. Именно такого рода отклонения происходят в любых макросистемах. Эти отклонения и обуславливают флуктуации.

Согласно теории вероятности, с увеличением числа N испытаний относительная флуктуация любой величины уменьшается по закону . Именно грандиозность числа N молекул и объясняет, почему макроскопические законы, получаемые на основе статистических представлений о движении частиц макросистемы, оказываются точными.

В дальнейшем будет использовано понятие бесконечно малого объема dV макросистемы. Под этим будет пониматься такой объем, размеры которого ничтожны по сравнению с размерами самой макросистемы, но все же намного превосходящие характерный размер ее микростроения. Каждая бесконечно малая область, предполагается, содержит число частиц dN настолько большое, что относительной флуктуацией их можно пренебречь.