1.6. Отношения

В математике часто пользуются для обозначения какой-либо связи между предметами или понятиями термином «отношение». Следующие неполные предложения (или предикаты) могут служить примерами отно­шений:

… меньше, чем…	… конгруэнтно…	… член…
… делится на…	… включено в…	… мать…

В настоящем параграфе понятие отношения будет освещено в рамках теории множеств.

Формулируемое ниже определение исходит из следующего предвари­тельного представления: (бинарное) отношение используется в связи с парами объектов, рассматриваемых в определенном порядке; оно касается существования определенного типа связи между некоторыми парами. Мы считаем при этом, что отношение дает критерий для отли­чения одних упорядоченных пар от других в следующем смысле. Если перечень всех упорядоченных пар, для которых имеет смысл говорить о данном отношении, задан, то с каждой такой парой мы связываем слово «да» или «нет» в качестве указания на то, что данная пара нахо­дится или, соответственно, не находится в рассматриваемом отношении. Оче­видно, что к этому же результату можно прийти, перечислив в точности те пары, которые находятся в данном отношении. Такой перечень пол­ностью характеризует данное отношение. Таким образом, для определения понятия отношения мы исходим из представления о множестве упорядо­ченных пар, для чего в свою очередь нужно предварительно уточнить понятие упорядоченной пары.

С интуитивной точки зрения упорядоченная пара — это просто сово­купность, состоящая из двух предметов, расположенных в некотором определенном порядке. Когда это понятие используют в математике, предполагают, что упорядоченная пара обладает двумя свойствами: (1) для любых двух данных предметов х и у существует объект, который можно обозначить через <x, y>, называемый упорядоченной парой х и у и однозначно определяемый предметами х и у; (2) если <x, y> и <u, v> — две упорядоченные пары, то <x, y> = <u, v> в том и только в том случае, когда x = u и у = v. Теперь мы можем определить объект (на самом деле являющийся множеством), который обладает обоими этими свойствами: упо­рядоченная пара предметов х и у, обозначаемая символически через <x, y>, есть множество

{{x}, {x, y}} ;

иначе говоря, это двухэлементное множество, один из элементов которого, {x, у}, есть неупорядоченная пара, а другой, {х}, определяет, какой из членов этой неупорядоченной пары считается «первым». Мы можем теперь, исходя из этого определения, доказать, что упорядоченные пары обладают обоими упомянутыми выше свойствами.

Т е о р е м а 1.4. Упорядоченная пара предметов х и у однозначно опре­деляется через х и у. Кроме того, если <х, у> = <u, v>, то х = и и y = v.

Д о к а з а т е л ь с т в о. То, что х и у однозначно определяют <x, у>, следует из принятого нами выше допущения, что множество однозначно определяется своими элементами. Обратимся ко второй части утвержде­ния. Пусть <х, у> = <u, v>. Рассмотрим два случая:

(I) u = v. Тогда <и, v> = {{u}, {и, v}} = {{u}}. Следовательно, {{x}, {x, у}} = {{u}}> из чего следует, что {х} = {х, у} = {и}, из чего, в свою очередь, вытекает, что х = и и y = v.

(II) u ≠ v. Тогда {и} ≠ {и, v} и {х} ≠ {и, v}. Поскольку {х}  {{и}, {и, v}}, то {х} = {и} и, следовательно, х = и. Поскольку {и, v}  {{x}, {x, у}} и {и, v} ≠ {х}, то {и, v} = {x, у}. Значит, {х} ≠ {х, у} и, далее, х ≠ у и у ≠ и. Окончательно, y = v.

Будем называть х первой координатой, а у — второй координатой упорядоченной пары <х, у>. В терминах упорядоченных пар можно определить теперь упорядоченные тройки и, вообще, упорядоченные n-ки. Упорядоченная тройка предметов х, у и z, обозначаемая через <х, у, z>, определяется как упорядоченная пара <<х, у>, z>. Если понятие упоря­доченной (n - 1)-ки уже определено, то упорядоченная п-ка¹ предметов х₁, х₂, . . . , х_п, обозначаемая через <x₁, х₂, . . ., х_п>, есть по определению << х₁, х₂, . . . , х_n-1>, х_п >.

Возвращаясь теперь к основной теме этого параграфа, мы определим бинарное (двуместное) отношение как множество упорядоченных пар, т. е. множество, каждый элемент которого есть упорядоченная пара. Если ρ есть некоторое отношение, то мы считаем выражения <x, y>  ρ и х ρ у взаимозаменяемыми и говорим, что х ρ-относится к у в том и только в том случае, когда х ρ у. Для некоторых отношений — например, равен­ства, принадлежности, включения, конгруэнтности — приняты специаль­ные обозначения. Такие привычные обозначения, как х = у, х < у и х ≡ y, исходят как раз не от обозначения <х, у>  ρ, а от х ρ у.

Естественным обобщением понятия бинарного отношения является понятие п-арного (п-местного) отношения, определяемого как множество упорядоченных n-ок. Термин «бинарное отношение» относился, разумеется, к случаю п = 2. Аналогично, вместо того чтобы говорить «3-арное отно­шение», мы будем пользоваться термином тернарное отношение.

Примеры А

1. Множество {<2, 4>, <7, 3>, <3, 3>, <2, 1>}, будучи множеством упорядоченных пар, есть бинарное отношение. Не имея никакого конкретного значения, это отношение, естественно, не получило и специального названия.

2. Отношение «меньше чем» для целых чисел есть множество {<x, у> | для целых чисел х и у найдется такое положительное целое число z, что x + z = y}. Если это отношение выразить символически обычным образом, предложения «2 < 5» и «<2, 5>  <» будут синонимичны (и оба истинны).

3. Если μ обозначает отношение материнства, то <Джейн, Джон>  μ означает, что Джейн является матерью Джона.

4. Отношение между родителями и ребенком представляет собой при­мер тернарного отношения. Если обозначить это отношение через ρ, то <Элизабет, Филип, Чарлз>  ρ означает, что Элизабет и Филип — родители Чарлза. Другой пример тернарного отношения дает нам опера­ция сложения в Z; запись «5 = 2 + 3» можно представить и в форме утверждения <5, 2, 3>  +.

¹ В качестве синонимов употребляются также термины «n-мерный вектор» и «кор­теж».— Прим. перев.

5. Отношение, связанное с операцией извлечения кубического корня из действительных чисел: {<x^1/3, x> | x  R}. Одним из элементов этого от­ношения является пара <2, 8>.

6. Функция «синус» в тригонометрии определяется посредством пра­вила, по которому каждому действительному числу сопоставляется неко­торое действительное число от —1 до 1. В практической работе часто используются специально изданные таблицы значений этой функции для различных значений аргумента. Такая таблица служит простым и компактным способом задания множества упорядоченных пар. Таким образом, для практических надобностей функция «синус» задается множеством упорядоченных пар чисел, представленным в виде таблицы (вместе с правилами пользования этой таблицей). Заметим, что такую таблицу можно изобразить в виде совокупности пар вида <х, sinx>; при этом существен порядок, в котором мы указываем координаты каждой пары. Для произ­вольного отношения ρ мы истолковываем запись <а, b>  ρ как выражающую тот факт, что а ρ-относится к b; в частности, наличие пары <π/2, 1> в таблице функции «синус» мы понимаем как сообщение о том, что первая координата этой пары синус-относится ко второй координате (вторая координата является синусом первой координаты).

В дальнейшем мы будем широко пользоваться тернарными отноше­ниями; пока же мы интересуемся бинарными отношениями; их мы и будем, если не возникнет опасности путаницы, называть просто «отношениями». Областью определения отношения ρ (обозначение: D_ρ) мы будем назы­вать множество {x | для некоторого у, <x, y>  ρ} областью значений отношения ρ (обозначение: R_ρ) — множество {у ‌ для некоторого х, <x, y>  ρ}. Иными словами, область определения отношения ρ — это мно­жество первых координат элементов из ρ, а область значений отноше­ния ρ — множество вторых координат элементов из ρ. Например, как областью определения, так и областью значений отношения включения для подмножеств множества U является множество (U), а, скажем, областью определения для отношения материнства служит множество всех матерей, в то время как область значений этого отношения — мно­жество всех людей¹. Один из простейших типов отношений — это мно­жество всех таких пар <x, y>, что x есть элемент некоторого фиксиро­ванного множества X, a y —элемент некоторого фиксированного множе­ства Y. Это отношение называется прямым² произведением множеств X и Y и обозначается через X*Y. Таким образом,

X*Y = {<x, y> | x  X и y  Y}.

Очевидно, каждое отношение ρ есть подмножество некоторого прямого произведения X*Y, такого, что Х  D_ρ и У  R_ρ. Если ρ — такое отношение, что ρ  X*Y, то говорят, что ρ есть отношение от X к Y. Если ρ — отношение от X к У и Z  X  Y, то ρ есть отношение от Z к Z. Отношения от Z к Z называют отношениями в Z.

¹ Если, конечно, с самого начала ограничиться рассмотрением этого отношения у людей.— Прим. перге.

² Или «декартовым».— Прим. перев.

Выражения «отношение от X к Y» и «отношение в Z» исходят из воз­можного применения понятия отношения к задаче отличения одних упорядоченных пар от других. Если X есть какое-то множество, то Х*Х есть некоторое отношение в X, которое мы назовем универсальным отно­шением в X; название это оправдывается тем, что для каждой пары х, у элементов из X имеет место x(Х*Х)у. Другим крайним примером слу­жит пустое отношение в X, совпадающее с пустым множеством. Проме­жуточное положение занимает тождественное отношение в X, обозначае­мое через ι или ι_x:{<x, х>| х  Х}. Очевидно, для любых х и у из X xι_Xy равносильно х = у.

Если ρ — отношение, а A — множество, то ρ[A] определяется как {у | для некоторого x из A хρу}. Это множество естественно называть множеством ρ-образов элементов множества A. Разумеется, ρ[D_ρ] = R_ρ и для произвольного множества A ρ[A]  R_ρ.

Примеры В

1. Если У ≠ , то Dx*y = X, и если Х ≠ , то Rx*y = Y.

2. Аналитическая геометрия плоскости основывается на допущении о возможности попарного соответствия между точками евклидовой плоскости и элементами множества R*R —множества упорядоченных пар действительных чисел. Таким образом, изучение геометрических конфигураций может быть сведено к изучению некоторых подмножеств множества R*R, т. е. отношений в R. Естественно ожидать, что для представляющих наибольший интерес геометрических конфигураций определяющими свой­ствами соответствующих им отношений в R будут служить алгебраические уравнения относительно х и у, неравенства, содержащие х и у, а также некоторые комбинации таких уравнений и неравенств. В таких случаях определяющее свойство отношения, связанного с какой-либо конфигурацией, относят обычно в качестве описания к самой этой конфигурации, а об отношении явным образом и не упоминают. Например, «прямая с уравнением у = 2х+1» есть сокращение для «множество точек, соответствующих множеству {<x, у>  R*R | у = 2х+1}». Аналогично «область, для которой у < x» — это множество точек, соответствующих мно­жеству {<х, у>  R*R | у < х}. Еще пример: соотношения

x≤0, у≥0 и у≤2х+1,

как легко проверит читатель, служат определением для некоторой плос­кой треугольной области.

Если основным предметом изучения служат не множества точек на плоскости, а сами по себе отношения в R, то множество точек, соответ­ствующих элементам отношения, называют графиком этого отношения (или графиком его определяющего свойства). Ниже (на рис. 7—10) при­водятся четыре примера отношений, для каждого из которых схемати­чески представлен его график. В тех случаях, когда график является частью плоскости, эта часть плоскости на чертеже заштриховывается.

Если ρ есть отношение в R с определяющим свойством 0 ≤ х ≤ 2, а σ — отношение в R с определяющим свойством 0 ≤ y ≤ 1, то отношение, иллюстрируемое рисунком 9, есть ρ  σ, а. отношение, иллюстрируемое рисунком 10, — ρ  σ. Таким образом, рисунки 9 и 10 иллюстрируют то обстоятельство, что график объединения двух отношений ρ и σ есть объединение графиков этих отношений, а график пересечения отношений ρ и σ есть пересечение их графиков.

Рис. 7. {<x, y>  R*R | y = x}.

y

0 x

Рис. 8. {<x, y>  R*R | y ≥ x}.

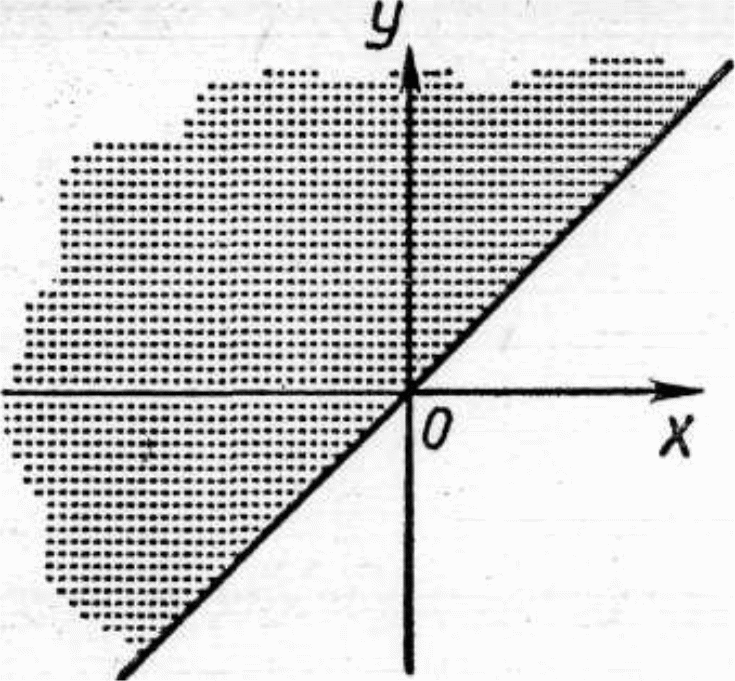
Рис. 9. {<x, y>  R*R | 0 ≤ x ≤ 2

или 0 ≤ y ≤ 1}

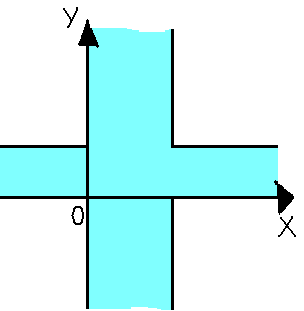
Рис. 10. {<x, y>  R*R | 0 ≤ x ≤ 2

и 0 ≤ y ≤ 1}

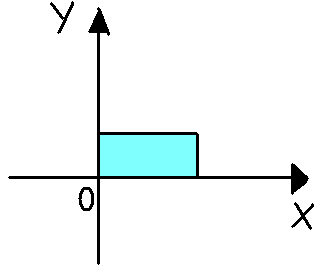
3. Пусть ρ — это отношение «быть отцом». Если A — множество всех нынешних жителей Соединенных Штатов, то ρ[A]—множество всех лю­дей, чьи отцы проживают в настоящее время в Соединенных Штатах, Если А — {Адам, Ева}, то ρ[A] = {Каин, Авель}.

Упражнения

1. Показать, что если <х, у, z> = <u, v, w>, то х = и, y = v и z=w.

2. Выписать элементы множества {1, 2}*{2, 3, 4}. Каковы область определения и область значений этого отношения? Что представляет собой его график?

3. Найдите область определения и область значений каждого из сле­дующих отношений, после чего постройте их графики:

(а) {<x, y>  R*R | x² + 4y² = 1};

(b) {<x, y>  R*R | x² = y²};

(с) {<x, y>  R*R | | x | + 2 | y | = 1};

(d) {<x, y>  R*R | x² + y² < 1 и x > 0};

(е) {<x, y>  R*R | y ≥ 0 и y ≤ x, и x + y ≤ 1}.

4. Представьте отношение из упражнения 3(с) в виде объединения четырех отношений, а отношение из упражнения 3(е) — в виде пересече­ния трех отношений.

5. Образование прямого произведения двух множеств есть бинарная операция над множествами («прямое умножение»). Покажите на приме­рах, что эта операция не является ни коммутативной, ни ассоциативной.

6. Пусть β — отношение «...есть брат...», а σ — отношение «...есть сес­тра...». Опишите отношения β  σ, β  σ и β — σ.

7. Пусть β и σ имеют те же значения, что в упражнении 6. Пусть А — множество студентов, обучающихся в настоящее время в том же ин­ституте, что и читатель. Что представляет собой β [А]? (β  σ)[А]?

8. Доказать, что для произвольных множеств А, В, С, D (А  В)* *(С  D) = (A*С)  (В*D). Доказать, что прямое умножение множеств дистрибутивно относительно операции пересечения, т. е. что для любых А, В и С {А  В)*С = (А*С)  (В*С) и А*(В  С) = (А*B)  (А*С).

9. Укажите такие четыре множества А, В, С и D, для которых (А  В)* (С  D) ≠ (А* С)  (В*Р).

10. Несмотря на результат предыдущего упражнения, прямое умно­жение дистрибутивно относительно операции объединения. Доказать.

11. Исследуйте, дистрибутивны ли объединение и пересечение относительно прямого умножения.

12. Доказать, что для любых непустых множеств А и В и любого множества С из (A*B)  (В*А) = С*С следует А = В = С.