§ 1.10. Отношения порядка

В этом параграфе мы определим несколько видов отношений, про­образом которых служит интуитивное понятие отношения порядка (пред­шествования—следования), т. е. такого отношения р, что в соответствующем множестве X

для некоторых пар его различных элементов х и у имеет место хру, но не урх. В этом случае при помощи отно­шения р можно решить, в каком порядке поставить эти элементы: х, у, а не y, х, так как имеет место хру, но не урх. Из такого рода от­ношений для множества действительных чисел хорошо известны отно­шения <, ≤, > и ≥. Аналогичную роль для систем множеств играют отношения  и .

Первый тип отношений порядка, который мы сейчас рассмотрим, будет характеризоваться основными свойствами, общими для упомянутых выше отношений ≤ для чисел и  для множеств. Предварительно мы введем одно понятие: отношение р во множестве X будет называться антисимметричным, если для любых элементов х и у множества X из одновременной истинности хру и урх следует x=у. Частичным упоря­дочением, или отношением частичного порядка, во множестве X мы будем называть рефлексивное, антисимметричное и транзитивное отношение в X. Поскольку можно пожелать рассматривать частичное упорядочение в X относительно некоторого другого, отличного от X множества (на­пример, обычное упорядочение в Z относительно множества четных чисел), удобно ввести еще одно определение: отношение р частично упорядочивает множество У, если р∩(УУ) есть частичное упорядочение в Y. Отношение р∩(УУ) есть «сужение» отношения р на множество У в том смысле, что оно исключает из рассмотрения те упорядоченные пары, у которых хотя бы одна из координат не есть элемент множества У.

Примеры.

1. Отношение «является целым кратным» в Z⁺ есть частичное упоря­- дочение.

2. Иерархия или схема организации в торговой фирме определяется частичным упорядочением в некотором множестве должностей.

3. Если р есть частичное упорядочение в X, то р ∩ (AA) частично упорядочивает подмножество А множество X.

4. Для любого отношения р обратным к нему называется такое

отношение р, что урх равносильно хру. Если р есть частичное упоря­дочение, то р также есть частичное упорядочение.

5. Любое рефлексивное и транзитивное отношение называется пред- упорядочением. Такого рода отношение может обладать тем неудобством, что при попытке упорядочить с его помощью какое-либо множество это отношение не позволяет «различать» некоторые пары различных объектов х, у—в том смысле, что будет иметь место как хру, так и урх. Напри­ мер, пусть для некоторого множества людей w будет функцией веса,

а h—функцией роста, т. е. w(x) и h(x) будут, соответственно, означать вес и рост некоторого индивида х. В таком случае отношение р такое, что xpу равносильно w(x)≤w(y) и h(x)≤h(у), будет предупорядочением, но не частичным упорядочением, если найдутся два индивида, имеющие одинаковый вес и одинаковый рост.

Если р есть предупорядочение множества X, то это отношение опре­деляет частичное упорядочение в некотором разбиении множества X (согласно упражнению 10 из § 1.7). Во-первых, утверждается, что отно­шение ~, для которого х~у равносильно по определению хру и урх, является отношением эквивалентности. Во-вторых, устанавливается, что отношеяие р', для которого [х] р' [у], если хру, является частичным упорядочением, областью определения которого служит соответствующее множество классов эквивалентности [х]. Окончательно можно сказать, что если р есть предупорядочение в некотором множестве X, то оно является частичным упорядочением в множестве, получающемся из X в результате идентификации элементов, не различимых с помощью отно­шения р.

Сказанное хорошо иллюстрируется следующим примером: в качестве р берется отношение во множестве комплексных чисел такое, что zpw, . если действительная часть числа г меньше или равна действительной части числа .

Следуя традиции, мы будем обозначать частичные упорядочения сим­волом ≤. Если отношение ≤ частично упорядочивает множество X, а х и у суть элементы множества X, то соотношение х ≤ у может иметь или не иметь места. Аналогично, если х ≤ у и ху, мы будем писать просто х < у и говорить, что х меньше, чем у, или х предшествует у, или у больше, чем х. Мы будем также использовать, если это нам почему-либо окажется удобным, записи ух и у>х в качестве альтернативы для х≤у и х <у соответственно.

Отношение р во множестве X является, по определению, иррефлексивным, если ни для какого х из X не имеет места хрх. Если ≤ — частич­ное упорядочение в X, то <—иррефлексивно и транзитивно в X. Обратно, исходя из иррефлексивного и транзитивного отношения < в X и полагая х≤у, по определению, равносильным х<у или х=у, мы приходим к частичному упорядочению ≤ в X. Доказательства этих фактов мы предоставляем читателю. Получение < из ≤С, и наоборот, может быть проиллюстрировано на примере определения строгого вклю­чения множеств в терминах включения и наоборот. Если ≤ частично упорядочивает конечное множество X, то отношение < можно описать посредством следующего понятия. Элемент у множества X, по

определению, покрывает элемент х, если х<у и не существует такого и, что х<и<_у. Если х<у, то, очевидно, можно найти такие элементы мно­жества Х:х₁, х₂, ..., х_п, что х = х₁ <х₂ < ... <x_n=y, причем каждое x_i+1 покрывает x_t. Обратно, из существования такой цепочки следует х<у.

Отношение р есть простое (или линейное) упорядочение, если оно является частичным упорядочением и, каковы бы ни были различные элементы х я у области определения (совпадающей с областью значений) отношения р, непременно имеет место либо хру, либо урх. Отношение р просто упорядочивает множество У, если p∩ (YY) есть простое упоря­дочение в У. Обычное упорядочение действительных чисел по величине есть типичный пример простого упорядочения. В противоположность этому включение множеств не является, вообще говоря, простым упо­рядочением.

Нечего и говорить, что отношения порядка применяются для уста­новления порядка в различных множествах. На практике отношение по­рядка для какого-либо данного множества X задается обычно постули­рованием или доказательством некоторых структурных характеристик множества X. Иными словами, определенные особенности строения мно­жества X, например существование операции или отображения какого-либо специального типа, позволяют определить для X отношение порядка; пример такого рода будет приведен в упражнениях к этому параграфу. Свойства такого отношения порядка могут оказаться полезными для выяснения и описания дальнейших характеристик множества X. Поэтому удобно располагать специальной терминологией, приспособленной в пер­вую очередь именно к множествам, а не к отношениям порядка в них.

Частично упорядоченное множество есть упорядоченная пара <Х, ≤ >, где отношение ≤ частично упорядочивает множество X. Просто упоря­доченное множество, или цепь, — это упорядоченная пара <Х, ≤ >, где ≤ просто упорядочивает множество X. Например, если F есть некото­рая система множеств, то <F, > есть частично упорядоченное множество. Если, далее, ≤ есть обычное упорядочение целых чисел, то <Z, ≤ > есть цепь. С точки зрения теории множеств более экономно рассматри­вать отношения порядка, а не упорядоченные множества (т. е. множе­ства вместе с упорядочивающими их отношениями). Если, скажем, <Х, ≤ > есть какое-то частично упорядоченное множество, то ≤ ∩(ХХ) есть частичное упорядочение в X. Поэтому вместо того, чтобы рассмат­ривать X и отношение ≤ , частично упорядочивающее X, нам достаточно рассматривать лишь само отношение порядка ≤ ∩(ХХ), поскольку оно полностью определяет X как область своего определения. Иначе говоря, для любого предложения об упорядоченных множествах можно

указать эквивалентное ему предложение об отношениях порядка и обратно.

В качестве иллюстрации предыдущего замечания мы переформулируем данное нами ранее описание отношения < для конечного множества X, частично упорядоченного отношением ≤ Пусть <Х, ≤ > есть конечное частично упорядоченное множество; тогда х < у равносильно тому, что существует цепь вида х=х₁<х₂<.... <.х_п =у, в которой каждое x_i+l покрывает X;. Это обстоятельство позволяет представить любое конечное частично упорядоченное множество в виде наглядной схемы. Элементы изображаемого множества X изображаются при этом точками, располо­женными на схеме в соответствии со следующим правилом. Точка, изо­бражающая у, располагается выше точки, изображающей х, в том и только в том случае, когда x<iy, причем, если у покрывает х, то х и у соеди­няются прямолинейным отрезком. Таким образом, х<

у равносильно тому, что на диаграмме имеется ломаная линия, восходящая от х к у. Вот несколько схем такого рода.

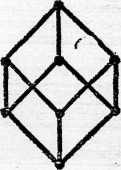
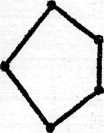
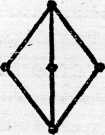
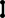
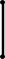
Н а первой схеме представлена цепь, состоящая из пяти элементов. Ясно, что схема любой цепи имеет такой вид. На последней схеме изо­бражено множество-степень трехэлементного множества, частично упоря­доченное посредством отношения включения; точка, расположенная на самом низком уровне, изображает пустое подмножество, точки, расположен­ные на следующем (втором снизу) уровне,—одноэлементные подмножества и т. д. Такие схемы используются не только для того, чтобы изображать уже заданные каким-либо образом частично упорядоченные множества, представляя в наглядном виде упорядочивающие их отношения; их можно использовать и для задания частично упорядоченных множеств — отно­шение порядка в этом случае, по определению, есть отношение, связы­вающее элементы, изображаемые точками, соединенными восходящими ломаными.

Перед тем как ввести еще одно определение, относящееся к понятию частично упорядоченного множества, нам будет полезно обсудить пред­варительно один пример. Множество {1, 2, 3, 5, 6, 10, 15, 30}, элементы

которого суть делители числа 30, частично упорядочено отношением ≤, где, по определению, х≤у, если у кратно х. Предлагаем читателю в ка­честве упражнения показать, что схема этого частично упорядоченного множества совпадает с последней из приведенных выше схем, изобра­жающей множество-степень трехэлементного множества, частично упоря­доченное отношением включения. Сами эти множества (множество-степень трехэлементного множества и множество делителей числа 30), разумеется, различны, но рассматриваемые с точки зрения их структуры—именно как частично упорядоченные множества — они неразличимы. Именно поэтому-то их схемы и совпадают. Этот тип отношений между двумя частично упорядоченными множествами заслуживает особого внимания, поскольку любому свойству каждого из таких множеств, формулируемому исключительно в терминах упорядочивающего его отношения, соответ­ствует совершенно аналогичное свойство другого множества. Поэтому мы хотим выразить такого рода «неразличимость» в точных формальных терминах. Тождество изображающих такого рода множества схем озна­чает, прежде всего, наличие некоторого соответствия, связывающего попарно элементы этих множеств. Это обстоятельство может быть опи­сано как существование взаимно-однозначного соответствия, что, кстати, удобно еще и тем, что мы не обязаны ограничиваться рассмотрением лишь конечных множеств. Интересующее нас соответствие между мно­жествами проявляется, далее, и в том, что любое соотношение между какой-либо парой ;элементов одного из множеств, полностью определя­емое его упорядочением, сохраняется и для соответствующей (в смысле упомянутого взаимно-однозначного соответствия) пары элементов другого множества (относительно аналогичного соотношения между членами этой пары, определяемого упорядочением этого второго множества). Точная формулировка рассматриваемого отношения между множествами фикси­руется следующим определением. Функция f : X→Х' называется сохра­няющей порядок (или изотопной) относительно упорядочения множе­ства X и упорядочения ≤' множества X', если х≤у влечет f (х) ≤' f (у). Теперь обсуждаемое нами подобие множеств можно описать как суще­ствование такого взаимно-однозначного соответствия, что оно само и обратное к нему сохраняют порядок. В этой связи принято пользоваться следующей терминологией. Изоморфизм между частично упорядоченными множествами <Х, ≤ > и <Х', ≤' > есть взаимно-однозначное соответствие между X и X' такое, что как оно, так и обратное к нему сохраняют порядок¹. Если такое соответствие существует, то одно из этих частично упорядоченных множеств называют изоморфным образом другого, или

¹ О более общем понятии изоморфизма см. ниже § 3.4 — Прим. перев.

говорят просто, что эти частично упорядоченные множества изоморфны. Таким образом, отношение «подобия», которое, как мы видели, имеет место между множеством всех подмножеств трехэлементного множества и множеством всех делителей числа 30, рассматриваемыми вместе с частич­ными упорядочениями этих множеств, можно описать, сказав, что эти множества суть изоморфные частично упорядоченные множества.

Когда выше мы определили понятие частично упорядоченного мно­жества, было отмечено, что типичным примером этого понятия является система множеств, частично упорядоченная включением. Конечно, это было сказано довольно-таки приблизительно—ведь смысл слова «типич­ный» имеет так много разных оттенков. Одно из возможных уточнений может быть дано в виде следующего важного утверждения: каждое частично упорядоченное множество изоморфно некоторой системе мно­жеств, частично упорядоченной включением. Это утверждение доказывает следующая

Теорема 1.7. Любое частично упорядоченное множество <Х, ≤ > изоморфно некоторой системе множеств, а именно некоторой системе подмножеств множества X, частично упорядоченной включением.

Доказательство. Для произвольного элемента а из X обозначим через S_a множество {xХ| x≤а}. Тогда отображение f, определенное на X со значениями в {S_aaX}, где f(a) = S_a, удовлетворяет утвер­ждению теоремы. Детали доказательства предоставляются читателю в качестве упражнения.

Этот результат часто формулируют так; «Каждое частично упорядо­ченное множество может быть представлено посредством некоторой си­стемы множеств (частично упорядоченной включением)». По сути дела, эта теорема означает, что изучение произвольных частично упорядочен­ных множеств можно без потери общности свести к изучению систем множеств, частично упорядоченных включением. На практике подобный перевод обычно все же не осуществляется, так как многие из непосредст­венно усматриваемых свойств конкретных частично упорядоченных мно­жеств при этом были бы утрачены. Отметим, наконец, что теорема 1.7 отнюдь не утверждает, что каждое частично упорядоченное множество изоморфно множеству всех подмножеств какого-либо множества. Такие частично упорядоченные множества (т. е. множества вида <P(A),>) не могут считаться типичными примерами произвольных частично упоря­доченных множеств, поскольку они обладают рядом специфических осо­бенностей. Например, любое такое множество содержит элемент (а именно, ø), меньший любого другого элемента, и элемент (а именно, А), боль­ший любого другого элемента.

В заключении этого параграфа мы введем еще несколько определений , относящихся к частично упорядоченным множествам, которые нам впоследствии понадобятся. Наименьшим элементом множества Х относительно частичного упорядочения ≤ мы будем называть такой элемент y множества Х, что для всех х из Х верно у ≤ х. Если такой элемент существует, то он единственен; поэтому, говорят о наименьшем элементе какого-либо множества Х относительно частичного упорядочения ≤ называют такой его элемент у, что ни для одного хХ не имеет места ч<у. Минимальный элемент может быть не единственным, как это видно, например, из второго из приведенных выше (стр.65) схем частично упорядоченных множеств. Наибольшим элементом множества Х относительно ≤ называют такой уХ, что для любого хХ х≤у. Наибольший элемент, если таковой существует, единственен, так что и в этом случае можно говорить о вполне определенном наибольшем элементе. Максимальным элементом множества Х относительно ≤ называют такой уХ, что ни для какого хХ не верно х>у.

Частично упорядоченное множество <X, ≤> называется вполне упорядоченным, если каждое непустое подмножество множества Х имеет наименьший элемент. Хорошо знакомым всем примером вполне упорядоченного множества является множество всех неотрицательных целых чисел, упорядоченное естественным образом. Каждое вполне упорядоченное множество <x, ≤> является цепью, так как для любых двух различных элементов х, у множества Х множество {x,. y} должно иметь наименьший элемент; следовательно, имеет место либо х<н, либо y<x.

Если <X, ≤ > есть частично упорядоченное множество и АХ, то элемент хХ называется верхней границей множества А, если для любого аА имеет место а≤х. Аналогично, элемент хХ называется нижней границей множества А, если для любого аА х≤а. Множество может иметь много верхних границ. Элемент хХ называется наименьшей верхней границей, или супремумом, множества А (в символах: sup А), если х есть верхняя граница множества А и для всех верхних границ у у множества А имеет место х≤у. Иными словами, наименьшая верхняя граница есть верхняя граница, являющаяся нижней границей множества всех верхних границ. Элемент хХ называется наибольшей нижней границей, или инфимумом, множества А (в символах: inf Ф), если х есть нижняя граница множества А и для любой нижней границы у множества А верно х>у. Легко видеть, что если множество А имеет наименьшую верхнюю границу, то она единственна; аналогично – для наибольшей нижней границы.

Упражнения

1. Доказать, что если р есть отношение частичного порядка, то об­- ратное отношение р также является отношением частичного порядка.

2. На множестве всех непрерывных функций, определенных на мно­- жестве неотрицательных действительных чисел и принимающих действии-­ тельные значения, f = O(g), по определению, означает: существуют такие положительные константы М и N, что для всех х> N f(x) ≤ Mg(x). По­- казать, что определенное таким образом отношение является предупо- рядочением, и определить соответствующее отношение эквивалентности.

3. Пусть ≤ есть частичное упорядочение множества X; доказать: < иррефлексивно и транзитивно в X. Пусть, обратно, < — отношение, иррефлексивное и транзитивное в X; доказать: отношение ≤ такое, что х≤ у равносильно х<у или х = у, есть частичное упорядочение в X.

4. Для каких множеств А <Р(А), > является линейно упорядо­- ченным множеством?

5. Пусть <Х, ≤ > и <Х', ≤' > — частично упорядоченные множества. Показать, что множество Х*Х' частично упорядочено отношением р, где <x, х'> р <у, у'>, по определению, равносильно х≤ y и x' ≤' у'. Ча­- стично упорядоченное множество <Х*Х', р> называют (прямым) про­ изведением данных частично упорядоченных множеств.

6. Двойственным к частично упорядоченному множеству <Х, р> на­ зывают частично упорядоченное множество <Х, р> (см. упражнение 1). Пусть <Х, ≤ > —частично упорядоченное множество, a,bX и а≤ b; множество всех таких х  X, что а≤ x≤ й, называют отрезком (замкну­ тым интерзалом) [а, b]. Показать, что множество отрезков частично упорядоченного множества <Х, ≤ > , частично упорядоченное включением, изоморфно некоторому подмножеству произведения частично упорядо­ ченного множества <Х , ≤ > и двойственного к нему.

7. Частично упорядоченное множество называют самодвойственным, если оно изоморфно двойственному к нему множеству. Доказать, что:

1. имеются в точности два неизоморфных частично упорядоченных двухэлементных множества, каждое из которых самодвойственно;

2. имеется пять попарно неизоморфных частично упорядоченных трехэлементных множеств, три из которых самодвойственны.

8. Показать на примере, что если <Х, ≤ > и <Х', ≤'> суть частично упорядоченные множества и f:X→X' — взаимно-однозначное соответ­ ствие, сохраняющее порядок, то f ^-1 может и не сохранять порядок.

9. Доказать, что если f есть изоморфизм между частично упорядо­ ченными множествами <Х, ≤ > и <Х', ≤'>, то х<у равносильно f(x)<'f(y).

10. Восполнить недостающие шаги доказательства теоремы 1.7.

11. Пусть <Х, ≤ > есть частично упорядоченное множество. Доказать, что и есть максимальный элемент тогда и только тогда, когда из уХ и yu следует у=и. Доказать, что v есть минимальный элемент тогда и только тогда, когда из уХ и y≤v следует y = v.

12. Пусть F_п есть система всех подмножеств множества Z⁺, имеющих не более п элементов (п—фиксированное положительное целое число), а F—совокупность всех конечных подмножеств множества Z⁺. Дока­ зать, что относительно включения

1. каждый элемент множества F _п, имеющий п элементов, максимален;

2. F не имеет максимальных элементов.

13. Пусть X — множество всех квадратов, лежащих внутри некото­ рого прямоугольника, не являющегося квадратом. Каковы максималь­ ные элементы этого множества относительно включения?

14. Доказать, что для линейно упорядоченного множества понятия наибольшего (наименьшего) и максимального (соответственно, минималь­ ного) элемента совпадают.

15. Пусть <Х, ≤ > — частично упорядоченное множество, обладающее тем свойством, что каждое его непустое подмножество, имеющее верх­ нюю границу, имеет наименьшую верхнюю границу. Доказать, что каж­ дое непустое подмножество множества X, имеющее нижнюю границу, имеет наибольшую нижнюю границу.

16. Доказать, что любое вполне упорядоченное множество <Х, ≤ > обладает свойством частично упорядоченного множества, сформулирован­ ным в условии предыдущего упражнения.

17. Пусть X — множество, р — операция в X. (Это значит, что р есть функция, определенная на Х*Х со значениями в X; значение функции р на <х, у> мы будем обозначать через ху.) Пусть, далее, р коммутативна, ассоциативна и идемпотентна [т.е. ху = ух, x(yz) = (xy)z и хх=х для всех х, у, zX]. Пусть, наконец, х≤у для х, уХ означает, по определению, ху =х. Доказать, что

1. ≤ частично упорядочивает X;

2. если X имеет наименьший элемент 0, то 0[: = 0;

3. ху≤ х; ху≤ у; из z≤ x и z≤ y следует xyz.

18. Отношение ≤, где m≤n означает, что п делится на т, частично упорядочивает множество Z⁺. Доказать, что любая пара целых чисел имеет относительно этого упорядочения наименьшую верхнюю границу и наибольшую нижнюю границу.

19. Доказать, что любое подмножество множества P(А), частично упорядоченного включением, имеет наименьшую верхнюю границу и наибольшую нижнюю границу.

1 Впрочем, это относится не ко всем математикам даже и того времени. См. ниже, главу III, особенно § 3.9.— Прим. перев

1 Употребителен также термин принцип экстенсиональности.— Прим. перев;

1 В оригинале — formula (формула); в переводе мы предпочли воспользоваться более подходящим (и употребительным) для данной цели термином «форма», тем бо­лее, что слову «формула» ниже (начиная с § 2.3) будет придаваться специальное зна­чение.— Прим. перев.

1 Принцип этот часто называют также принципом свертывания; в формулировке его обычно говорят не о форме, a d формуле, но мы (см. предыдущее примеча­ние) предпочитаем резервировать этот термин для обозначения формальных выраже­ний определенного вида (см. §§ 2.3, 2.7 и особенно 3.8).— Прим. перев

1 Разумеется, речь идет о сенате США — Прим. перев. и ред

1 Здесь мы пользуемся обозначением, подробно обсуждаемым ниже.

1 См. §§ 2.1 и 2.2. —Прим.. пгрев.

1 Читатель, возможно, привык к использованию различных терминов для наименования какой-либо операции и ее результата: «умножение» — «произведение», «сложение»—«сумма», «вычитание» — «разность». В этой книге во многих случаях (хотя и не всегда) для обоих понятий используется один термин; к двусмысленностям это не приводит, поскольку из контекста ясно, о чем именно идет речь.— Прим. перев.

2 Под «рассуждением» здесь может пониматься и целая книга или даже некото­рая научная теория; ср. ниже авторские примеры. Вместо «универсальное множество» часто говорят «универсум рассуждения» или просто «универсум».— Прим. перев.

3 Этот способ изображения отношений между множествами (или классами, поня­тиями, свойствами) известен также под именем «кругов Эйлера».— Прим. перев