Обратная матрица.

Для любого действительного числа существует обратное число такое, что . Для квадратных матриц вводится аналогичное понятие.

• Определение. Матрица 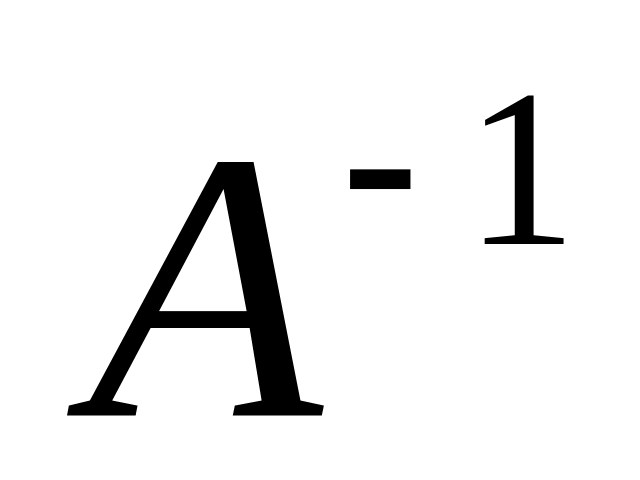называется обратной по отношению к квадратной матрице , если при умножении этой матрицы на обратную, как справа, так и слева получается единичная матрица:

.

Из определения следует, что только квадратная матрица имеет обратную; при этом обратная матрица также является квадратной того же порядка. Однако не каждая квадратная матрица имеет обратную.

Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная .

Алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы. Если 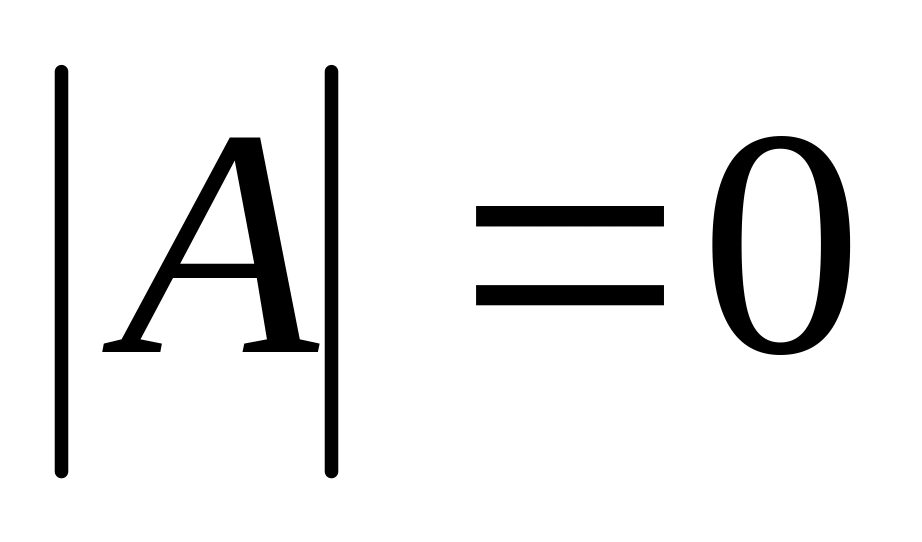, то матрица - вырожденная и не имеет обратной матрицы.

2. Находим матрицу - транспонированную к матрице .

3. Находим алгебраические дополнения элементов транспонированной матрицы 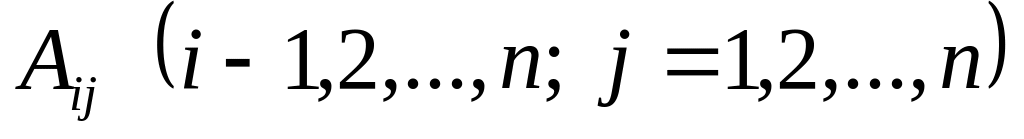и составляем из них матрицу, заменяя каждый элемент матрицы его алгебраическим дополнением. Такая матрица называется присоединенной (или союзной), обозначим ее .

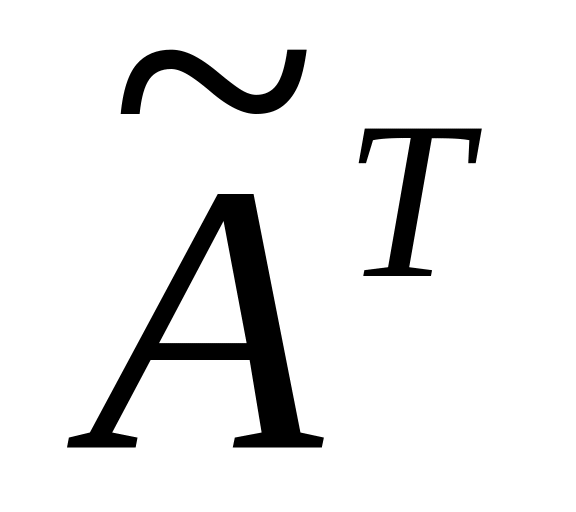4. Вычисляем обратную матрицу по формуле .

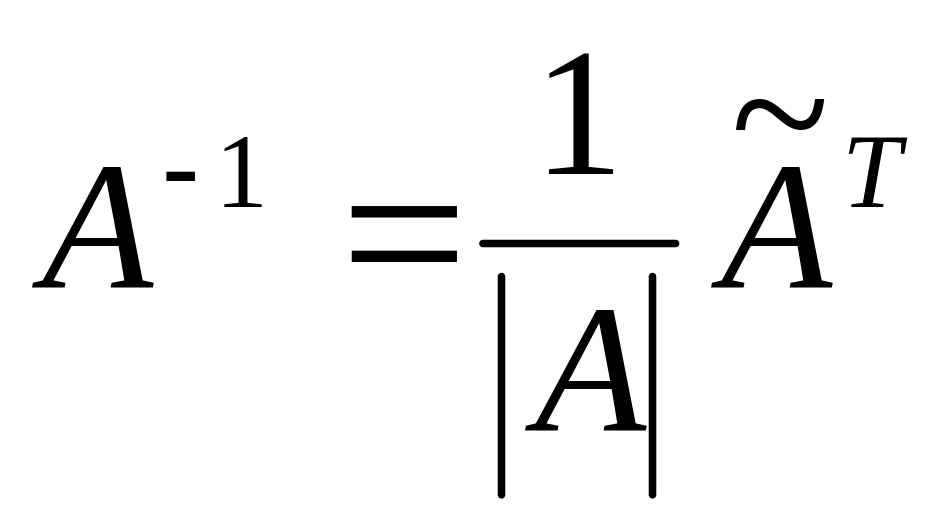5. Проверяем правильность вычисления обратной матрицы , исходя из её определения: .

Пример 1. Найти матрицу, обратную данной .

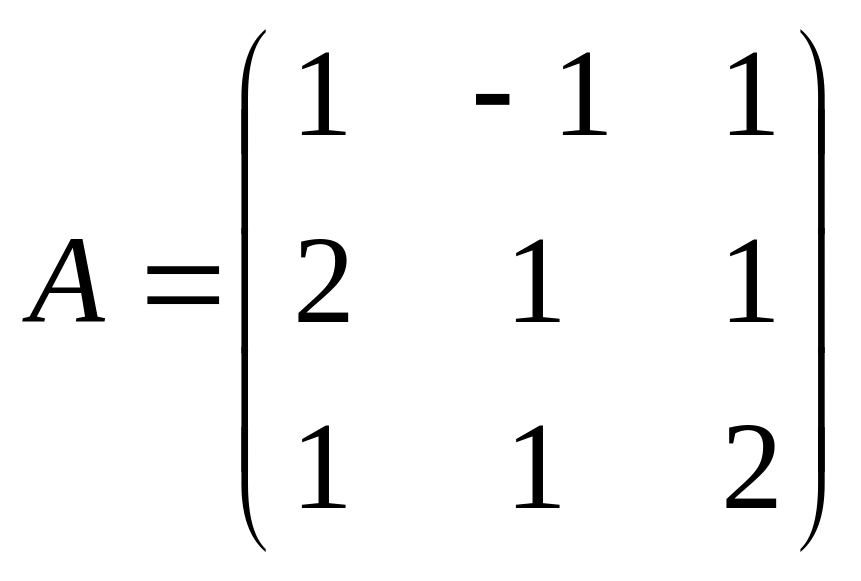1. Найдем определитель матрицы разложением по первой строке =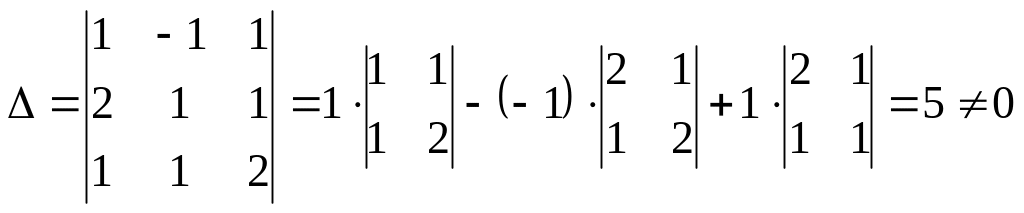 , следовательно, матрица А невырожденная и обратная матрица существует.

2. Находим матрицу , транспонированную к А:

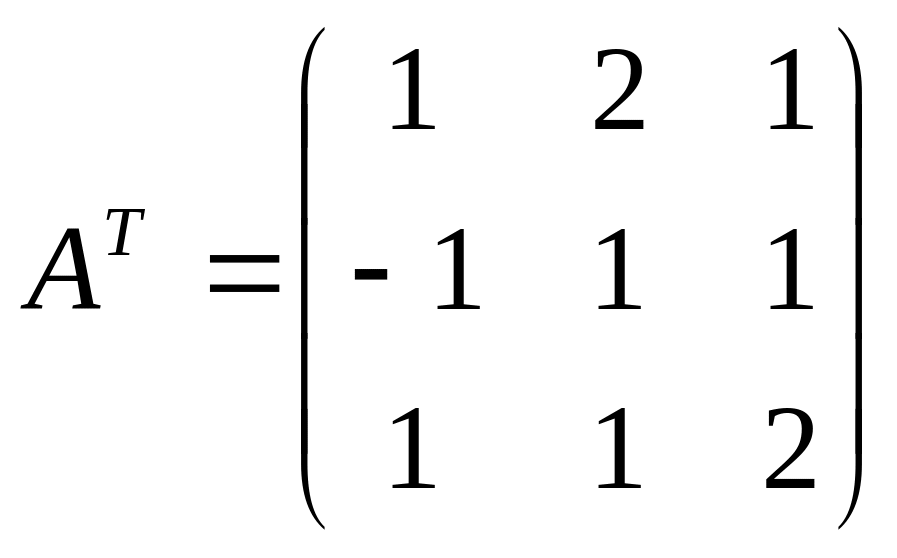
3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу:

.

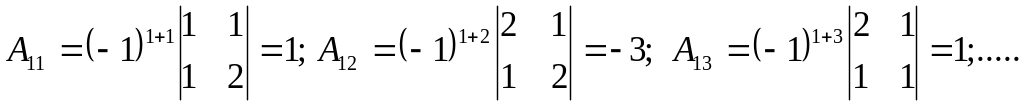
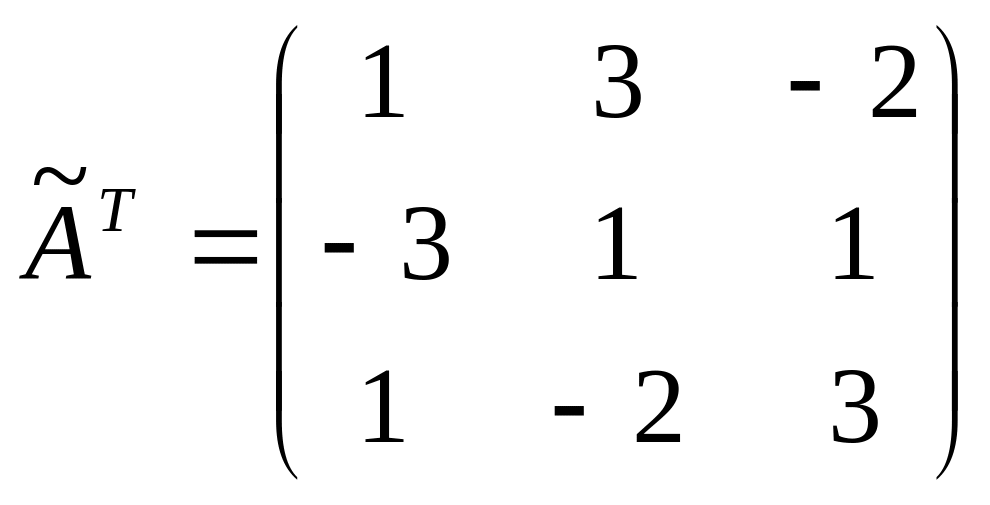4. Вычисляем обратную матрицу .

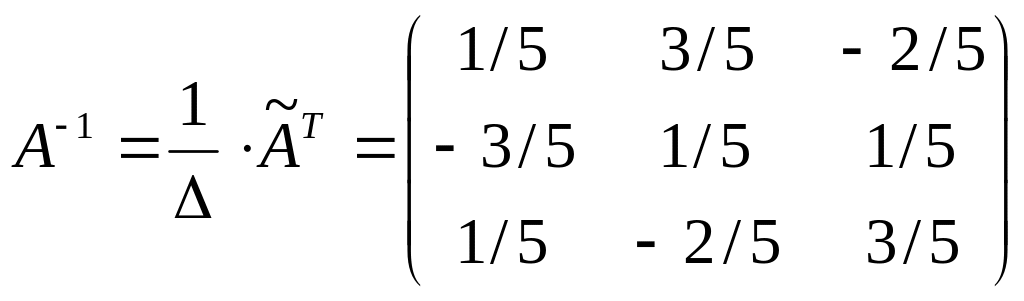5. Проверяем правильность вычисления обратной матрицы по формулам: (выполнить самостоятельно).

2. Системы линейных уравнений.

Пусть дана система т линейных уравнений относительно п неизвестных . Уравнения системы пронумеруем: первое, второе и т.д. Коэффициенты при неизвестных в -том уравнении системы обозначим через (первый индекс указывает номер уравнения, второй – номер неизвестного, при котором стоит этот коэффициент), а свободный член -того уравнения – через . Тогда система будет иметь вид:

(1)

Числа называются коэффициентами системы уравнений, а числа - свободными членами. Заметим, что в системе уравнений (1) количество неизвестных может не совпадать с числом уравнений.

• Решением системы уравнений (1) называется такая последовательность чисел 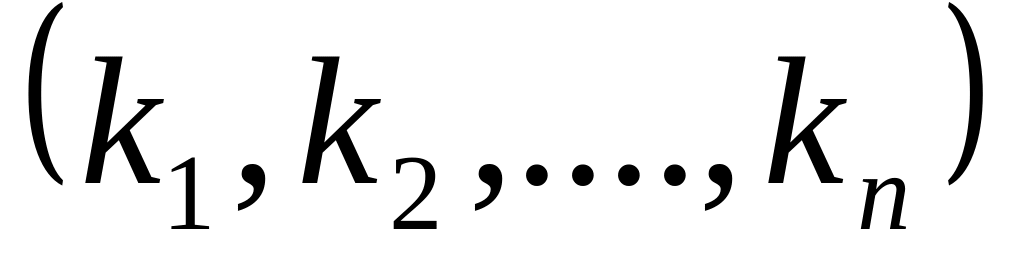, которая является решением каждого уравнения системы. Решить систему – значит найти все ее решения или убедиться в том, что их нет.

Возможны только три случая:

1) система уравнений несовместна, т.е. не имеет ни одного решения;

2) система уравнений является определенной, т.е. имеет единственное решение;

3) система уравнений является неопределенной, т.е. имеет бесчисленное множество решений.

• Система, имеющая хотя бы одно решение, называется совместной.

• Неизвестное 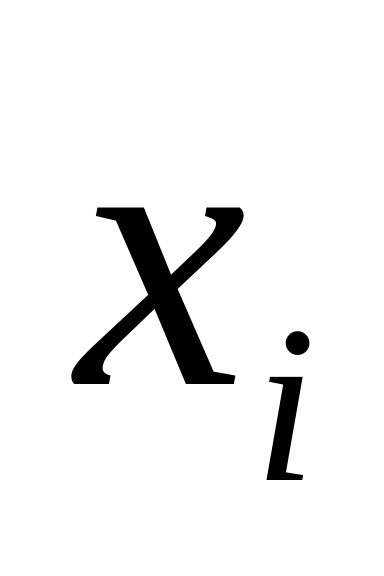называется разрешенным, если какое-нибудь уравнение системы содержит это неизвестное с коэффициентом, равным единице, а во все остальные уравнения системы неизвестное не входит, т.е. входит с коэффициентом, равным нулю.

Например, система уравнений

содержит разрешенные неизвестные , неизвестные же не являются разрешенными.

• Если каждое уравнение системы содержит разрешенное неизвестное, то такую систему называют разрешенной. Так система, приведенная выше, является разрешенной.

Из каждого уравнения разрешенной системы выберем по одному разрешенному неизвестному, получим набор попарно различных неизвестных, который называется набором разрешенных неизвестных данной системы. Заметим, что набор разрешенных неизвестных в общем случае определен неоднозначно. Например, приведенная в примере система обладает двумя наборами разрешенных неизвестных и .

Неизвестные системы линейных уравнений, которые не входят в данный набор, называются свободными. Так, если в системе - набор разрешенных неизвестных, то неизвестные являются свободными, если же - набор разрешенных неизвестных, то свободными являются неизвестные .

• Разрешенная система уравнений всегда совместна.

• Система будет определенной, если число уравнений равно числу неизвестных, и неопределенной, если количество неизвестных больше числа уравнений.