- •I. Обыкновенные дифференциальные уравнения (оду)
- •Линейные уравнения. Теорема о существовании и единственности решения задачи Коши для линейного уравнения n-го порядка.
- •Линейно зависимые и линейно независимые системы функций. Определитель Вронского.
- •4. Необходимое и достаточное условие линейной независимости системы решений линейного однородного уравнения.
- •5. Фундаментальная система решений (фср) линейного однородного уравнения. Теорема о существовании фср.
- •6. Теорема о представлении общего решения линейного однородного уравнения.
- •7. Структура общего решения линейного неоднородного уравнения.
- •II. Системы оду.
- •8. Системы уравнений в нормальной форме. Задача Коши. Теорема о решения задачи Коши для системы в нормальной форме.
- •9. Линейные системы. Теорема о решения задачи Коши для линейной системы.
- •10. Линейно зависимые и линейно независимые системы вектор-функций. Определитель Вронского.
- •11. Необходимое и достаточное условие линейной независимости решений линейной од-нородной системы уравнений.
- •12. Фср для системы линейных уравнений. Теорема о существовании фср.
- •13.Теорема о представлении общего решения линейной однородной системы.
- •14.Структура общего решения линейной неоднородной системы.
- •III. Автономные систему оду
- •16. Фазовое пространство и фазовые траектории автономной системы.
- •17. Первые интегралы однородной системы. Достаточное условие первого интеграла. Теорема о существовании независимых первых интегралов.
- •18. Устойчивость по Ляпунову и асимптотическая устойчивость положения равновесия автономной системы. Условие асимптотической устойчивости положения равновесия линейной системы.
- •19. Линеризация нелинейной системы в окрестности положения равновесия. Условие асимптотической устойчивости положения равновесия нелинейной системы.
- •20. Фазовые портреты линейных однородных систем с постоянными коэффициентами на плоскости: случаи узла, седла, фокуса и центра.
- •21. Фазовые портреты нелинейных систем. Исследование положения равновесия нелинейной системы на плоскости по линейному приближению. Предельные циклы.
- •22. Фазовая плоскость оду 2-го порядка. Пример: математический маятник.
- •23. Линейные и квазилинейные учп 1-го порядка. Представление общего решения через первые интегралы системы уравнений характеристик.
14.Структура общего решения линейной неоднородной системы.
Решение неоднородной системы: ,
для
функции
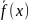 специального
вида укажем в каком виде нужно искать
частное решение.
специального
вида укажем в каком виде нужно искать
частное решение.
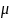 – не
является корнем характеристического
уравнения.
– не
является корнем характеристического
уравнения.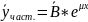 ,
где
,
где
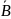 – постоянный (неопределенный столбец).
– постоянный (неопределенный столбец).– корень характеристического уравнения кратности s.
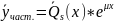 ,
где
,
где
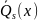 – столбец, элементы которого многочлены
степени sс
неопределенными коэффициентами.
– столбец, элементы которого многочлены
степени sс
неопределенными коэффициентами.
 ,
где
–корень
характеристического уравнения кратности
s,
,
где
–корень
характеристического уравнения кратности
s,
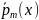 – столбец, элементы которого многочлены
и m
– maxстепень.
– столбец, элементы которого многочлены
и m
– maxстепень.
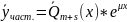
III. Автономные систему оду
1.
Определение:
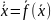 (1)
(1)
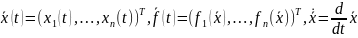
Предположение:
функции
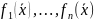 удовлетворяют условию теоремы о
единственности в некоторой области
удовлетворяют условию теоремы о
единственности в некоторой области
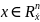 ,
т. е. непрерывны и дифференцируемы в т.
x.
,
т. е. непрерывны и дифференцируемы в т.
x.
Замечание:
неавтономная система
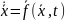 превращается
в автономную, если положить
превращается
в автономную, если положить
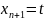 ,
т.е.
,
т.е.
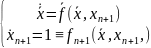
16. Фазовое пространство и фазовые траектории автономной системы.
Пусть
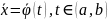 - решение интеграла (1). В
- решение интеграла (1). В
 это решение задает кривую
это решение задает кривую
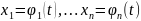 ,
,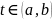 -
параметр кривой, называемой фазовой
траекторией системы (1), при этом
пространство
- фазовое пространство системы(1).
-
параметр кривой, называемой фазовой
траекторией системы (1), при этом
пространство
- фазовое пространство системы(1).
Фазовая
траектория получается проектированием
на
(вдоль оси t)интегральной
кривой, лежащей в
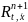 .
.

Свойства фазовых траекторий
1)
Если
 -
также решение. Фазовые траектории
соответствующие этим решениям совпадают.
-
также решение. Фазовые траектории
соответствующие этим решениям совпадают.
Док-во: ,
т.е.
,
т.е.
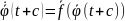 ч.т.д.
ч.т.д.
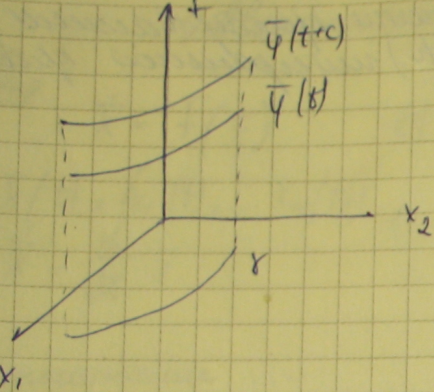
2) Любые две фазовые траектории системы (1) либо не имеют общих точек либо совпадают.
Док-во:
Пусть
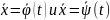 - решения системы (1). Пусть соответственно
- решения системы (1). Пусть соответственно
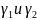 имеют
общую точку
имеют
общую точку
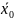 ,
т.е.
,
т.е.
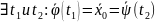 .
.
Рассмотрим
решение
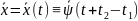 .при
t=
.при
t=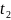 имеем
имеем
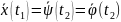 .
По Теореме о
.
По Теореме о
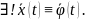 Фазовые
траектории
.
и реш.
Фазовые
траектории
.
и реш.
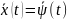 совпадают
по св-ву 1.
совпадают
по св-ву 1.
Определение:
точка
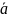 называется положением равновесия
системы (1) если
называется положением равновесия
системы (1) если
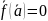 .
.

3)
Если
-
положение равновесия сестемы (1), то
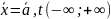 - стационарное решение системы (1).
Соответственно фазовая траектория
состоит из одной точки то
- стационарное решение системы (1).
Соответственно фазовая траектория
состоит из одной точки то
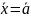
4) Всякая фазовая траектория принадлежит к одному из следующих 3х типов:
гладкая кривая без самопересечений
замкнутая гладкая кривая(цикл)
точка положения равновесия.
17. Первые интегралы однородной системы. Достаточное условие первого интеграла. Теорема о существовании независимых первых интегралов.
Функция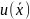 называется
первым интегралом системы (1), если на
любом решении
называется
первым интегралом системы (1), если на
любом решении
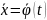 системы(1) она постоянна, т.е
системы(1) она постоянна, т.е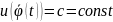 (2)
(2)
Пример:
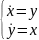 П.И:
П.И:
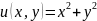
Iспособ:
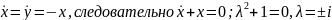
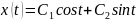

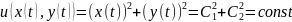
IIспособ:
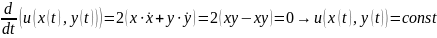
Критерий
первого интеграла:
пусть
-
некоторая функция(гладкая).
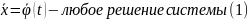 ,
тогда
,
тогда
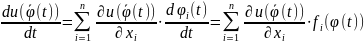
Выражение
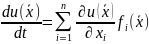 (3)
называется производной функцией
в
силу системы (1)
(3)
называется производной функцией
в
силу системы (1)
Теорема:
функция
является
первым интегралом системы (1), тогда и
только тогда когда она удовлетворяет
условию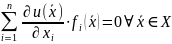 (4)
(4)
Док-во:
1) если (4) выполнено в Х, то оно выполнено
и в точках любой траектории
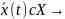 для
любого решения
для
любого решения
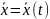 правая
часть (3)
правая
часть (3)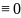 =>
левая часть (3))
,
т.е.
=>
левая часть (3))
,
т.е.
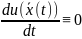 ,
т.е.
,
т.е.
 - первый интеграл системы (1).
- первый интеграл системы (1).
2)
Пусть
- первый интеграл системы (1). По теореме
о существовании единственности:
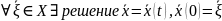 .
.
т.к.
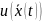 =const,
то
=const,
то
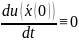 и в силу (3)
и в силу (3)
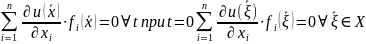
Теорема
(о независимых первых интегралах) пусть
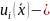 непрерывно дифференцируемые функции
в
непрерывно дифференцируемые функции
в
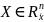 .
Эти функции называются зависимыми в
области Х, если одну из них можно выразить
из остальных.
.
Эти функции называются зависимыми в
области Х, если одну из них можно выразить
из остальных.
Теорема:
пусть точка
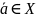 не является положением равновесия
системы (1), тогда в некоторой
окрестности
не является положением равновесия
системы (1), тогда в некоторой
окрестности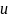 (
)система
(1) имеет n-1
независимых первых интегралов и всякий
п.и. этой системы представляется в виде
(
)система
(1) имеет n-1
независимых первых интегралов и всякий
п.и. этой системы представляется в виде
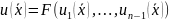 ,
где F
- некоторая
гладкая функция.
,
где F
- некоторая
гладкая функция.