Тема 4. Метод математической индукции. Элементы комбинаторики Сведения из теории

Одной из отличительных черт математики и таких наук, как теоретическая механика, математическая лингвистика, является дедуктивное построение теории, при котором все утверждения выводятся из нескольких основных положений, называемых аксиомами, с помощью дедукции, т. е. логического вывода (само слово “дедукция” по-русски означает “вывод”). Аксиомами называют высказывания, задающие свойства основных понятий данной теории и отношений между этими понятиями.

Однако дедукция не является единственным методом научного мышления. Уже в вычислительной математике не всегда удается строго доказать, что вычислительные процессы сходятся и их применимость обосновывается тем, что они дают, как правило, результаты, подтверждаемые практикой. Еще шире используется апелляция к наблюдению и опыту в таких науках, как физика, химия, биология. В них наряду с дедукцией широко используются индуктивные рассуждения. Слово “индукция” по-русски означает “наведение”, а индуктивными называют выводы, сделанные на основе наблюдений, опытов т. е. полученные путем заключения от частного к общему.

Индукция может привести и к ошибочным выводам. Например, французский математик XVII века Пьер Ферма, рассматривал числа , , , , и пришел к выводу, что при любом натуральном значении число является простым. Проверить справедливость этого утверждения при он не смог, т. к. не сумел выяснить, имеет ли число нетривиальные делители, т. е. делители, отличные от 1 и от самого числа .

Но Эйлеру удалось показать, что число делится на 641, т. е. оно не является простым.

Из сказанного следует, что это указанный с помощью индукции результат подлежит дедуктивному доказательству. В некоторых случаях такое доказательство можно провести, разобрав конечное число случаев, исчерпывающих все возможности.

Например, чтобы доказать утверждение: для любого правильного многогранника справедливо соотношение , где – число его вершин, – ребер, – граней, достаточно рассмотреть 5 случаев известных правильных многогранников: тетраэдр, октаэдр, куб, додекаэдр, икосаэдр (других правильных многогранников не существует). А для этих пяти случаев утверждение проверяется с помощью следующей таблицы.

Название	число вершин	Число ребер	Число граней
Тетраэдр Октаэдр Куб Додекаэдр Икосаэдр	4 6 8 20 12	6 12 12 30 30	4 8 6 12 20

Во всех случаях имеем: .

Такой метод перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией.

Метод полной индукции имеет весьма ограниченную область применимости в математике. Как правило, математические утверждения касаются бесконечного множества объектов и перебрать все эти объекты оказывается невозможным. Но существует метод рассуждения, заменяющий неосуществимый перебор бесконечного множества случаев доказательством того, что если данное утверждение истинно в одном случае, то оно окажется истинным и в следующем за ним случае. Такой метод рассуждения называется математической индукцией или рассуждением от к .

При доказательстве комбинаторных теорем нам понадобится часто употребляемая теорема, называемая обычно принципом полной математической индукции, состоящая из следующих положений:

1) некоторое утверждение, зависящее от натурального параметра n справедливо при ,

2) из справедливости утверждения для всех натуральных значений параметра от 2 до произвольных включительно следует его справедливость для , то утверждение справедливо для любого натурального значения параметра .

Итак, для доказательства утверждения , зависящего из натурального параметра , методом полной математической индукции необходимо:

1. проверить справедливость этого утверждения для , т. е. убедится, что 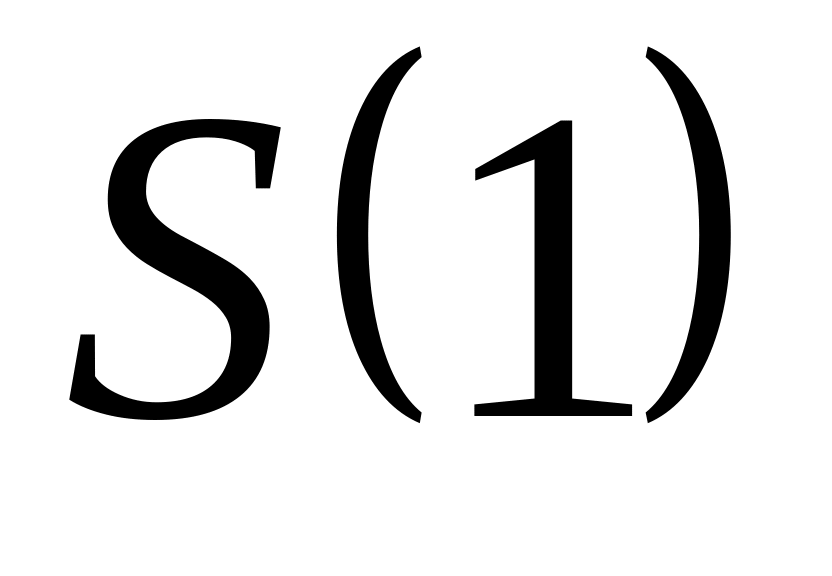 – истина;

2. предположить справедливость этого утверждения для всех натуральных значений n от 2 до k включительно, в частности предположить, что  – истина;

3. проверить справедливость утверждения для , т. е. проверить, что 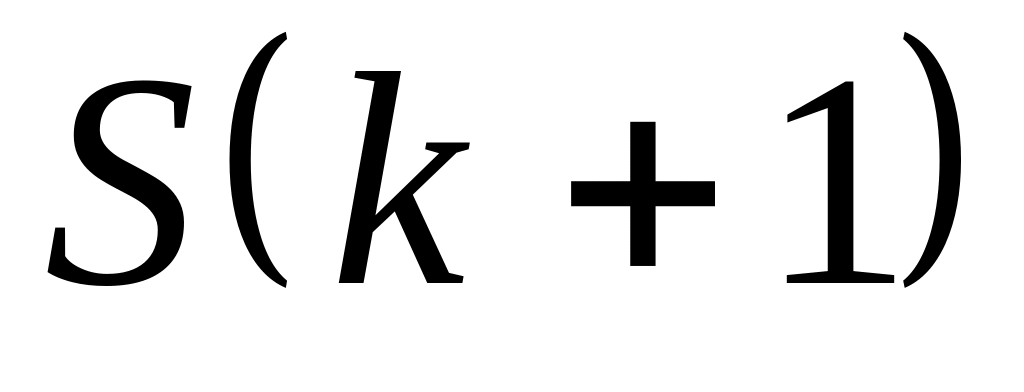 – истина;

Например, требуется доказать, что при любом натуральном число делится на 3.

1. Проверим, верно ли утверждение при , т. е. проверим, делится ли на 3 число : .

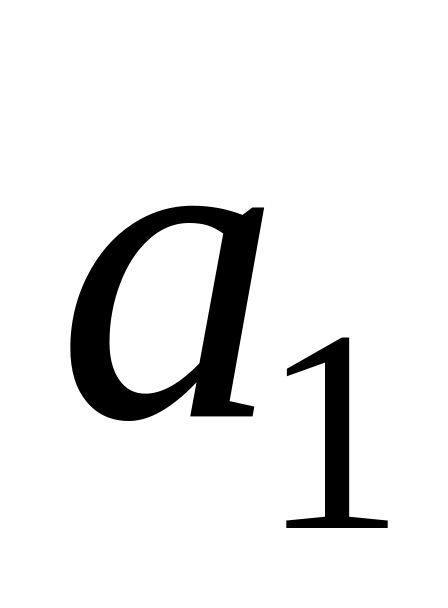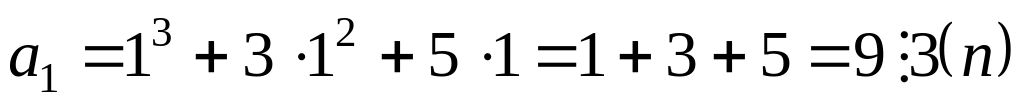2. Предположим, что утверждение верно для всех натуральных n от 2 до k включительно, в частности, предположим, что .

3. Проверим, делится ли на 3 число .

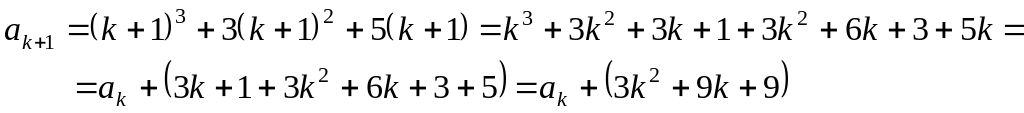
(по предположению); (по свойствам делимости). Значит, (по свойствам делимости).

Согласно метода полной математической индукции мы можем утверждать, что число делится на 3 при любом натуральном значении .

Доказательство методом неполной математической индукции некоторого утверждения, зависящего от натурального параметра , начиная с некоторого натурального , проводится следующим образом:

1. Устанавливается справедливость этого утверждения для .

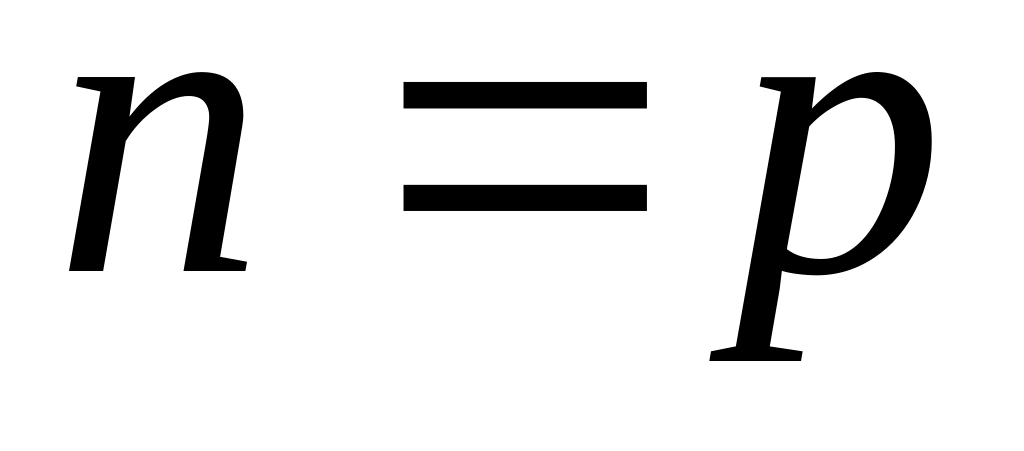2. Предполагается справедливость этого утверждения для всех натуральных значений от 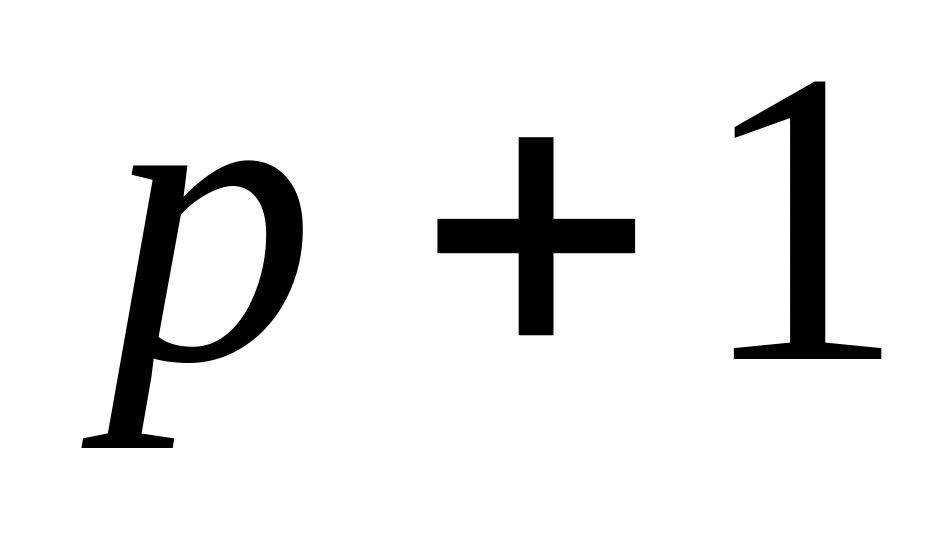до ( – любое натуральное число, не меньше ).

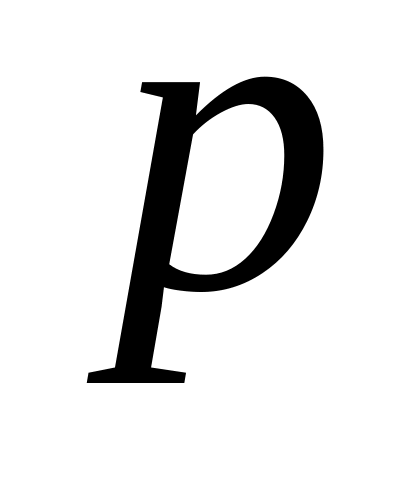3. Устанавливается исходя из (2) его справедливости для .

На основании (1) и (2) и принципе неполной математической индукции делается вывод, что это утверждение справедливо для любого натурального .

Распространенными задачами комбинаторики являются задачи о числе различных соединений: размещений, перестановок, считаний, и задачи, связанные с формулой Ньютона (биномом Ньютона).

Одно из важных правил комбинаторики – правило умножения. Если объект может быть выбран способами, затем для каждого из таких типов выборов объекта другой объект может быть выбран способами, затем для каждого из таких выборов и объекта и объекта третий объект может быть выбран способами и т. д., включая -ый объект , который может быть выбран способами , то объект, состоящий в выборе всех m объектов вместе, т. е. объект “ , , ” может быт выбран способами.

Пример 1. Сколько трехзначных четных чисел можно составить их цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться ?

Решение.

При составление трехзначного четного числа , , из данных цифр вместо можно взять любую указанную цифру кроме 0 (6 возможностей), вместо можно взять любую из этих цифр (7 возможностей), вместо можно взять любую из цифр 0, 2, 4, 6 (4 возможности).

Согласно правилу умножения, имеется способов составить число, удовлетворяющее условию задачи.

Пример 2. Сколько существует шестизначных чисел, которые делятся на 5?

Решение.

Поскольку число делится на 5, то его цифра разряда единиц равна 0 или 5 (2 возможности). Цифры же разряда десятков, сотен, тысяч и десятков тысяч могут быть любыми от 0 до 9, т. е. в каждом из этих случаев имеется 10 возможностей. Цифра разряда сотен тысяч шестизначного числа может быть любой, кроме 0 (9 вариантов).

Следовательно, всего несколько чисел 9∙10∙10∙10∙102=180000.

Для любого натурального числа n произведение 1.2…..n обозначается n ! (читается “эн факториал”), т. е. 1.2…..n = n !.

Кроме того полагает О !, 1!=1.

Другими словами: n ! =

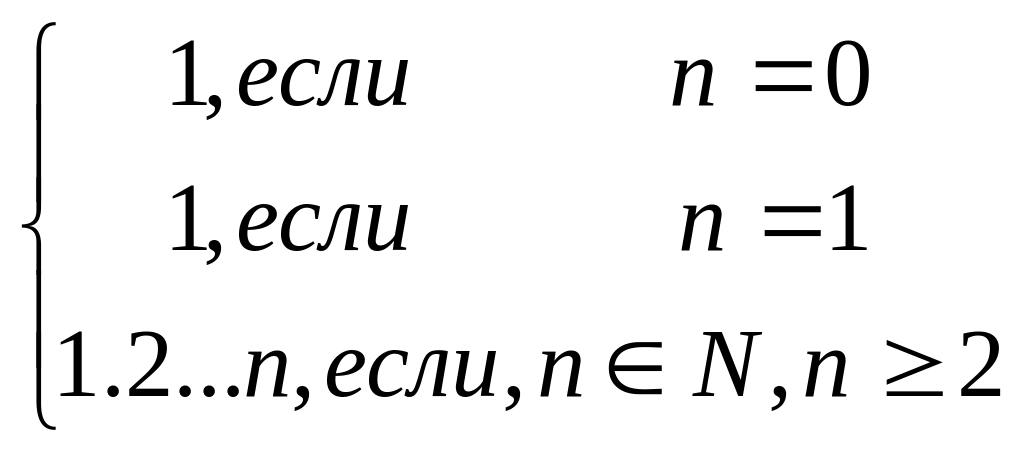
Например: 1!=1

2!=1∙2=2

3!=1∙2∙3=6

4!= 1∙2∙3∙4=24

10!=1∙2∙3∙4∙5∙6∙7∙8∙9∙10=720∙7∙8∙9∙10=720∙5040=3628800

При выборе m элементов из n различных элементов принято говорить, что они образуют соединение из n элементов по m .

В зависимости от того, имеет ли значение порядок элементов в соединение или нет, а также от того, входят в соединение все n элементов или только часть их, различают три вида соединений: перестановки, сочетания, размещения. Любое упорядоченное подмножество элементов, взятых из данного множества, называется размещением.

Из этого определения вытекает, что размещение одного и того же множества отличаются друг от друга либо элементами, входящими в них, либо их взаимным расположением, либо и элементами и взаимными расположениями этих элементов.

Например, для множеств подмножества , , являются размещениями.

Столькими способами можно выбрать и разместить по различным местам из различных предметов? Количество всех таких способов принято обозначать (читается “число размещений из эн по эм”) и .

Например, выпишем все размещения множества по два: , , , , , , , , , , , . Получилось 12 размещений. В этом случае , и .

Перестановкой элементов множества называется любое их взаимное расположение. Из этого определения следует, что каждая перестановка множества содержит в себе все элементы этого множества. В этом заключается существенное отличие перестановки от размещения элементов одного и того же множества. Другими словами, перестановка множества длины есть размещение такой же длины .

Поэтому число перестановок n элементов, обозначаемое символом , можно посчитать по формуле:

.

Например, для множества имеется 3!=6 различных перестановок: , , , , , .

Подмножества данного множества , отличающиеся друг от друга хотя бы одним элементом, называются сочетаниями элементов этого множества.

Из этого определения следует, что в сочетаниях взаимное расположение элементов во внимание не принимается. Например, для множества подмножества и представляет собой одно и то же сочетание.

Число сочетаний из элементов по элементов обозначается символом (читается “число сочетаний из эн по эм”) и может быть вычислено по формуле:

=

Например, .

Действительно, если , то сочетаниями будут являться подмножества , , , , , , , , , .

Числа обладает целым рядом замечательных свойств:

1) =

2)

3)

Последнее тождество позволяет вычислить значения , зная и . Иными словами, с помощью этого тождества можно последовательно вычислить сначала при , затем при , при и т. д.

Вычисления удобно записывать в виде треугольной таблицы:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

В -й строке таблицы по порядку стоят числа , , …, . При этом = =1, а остальные числа вычисляются по формуле = + . Поскольку и располагаются в этой таблице строкой выше, чем , и находятся в этой строке слева и справа от него, то для получения надо сложить находящиеся слева и справа от него числа предыдущей строки. Например, значение 10 в шестой строке мы получим, сложив числа 4 и 6 пятой строки.

Другими словами, мы имеем таблицу:

Эту треугольную таблицу называют треугольником Паскаля по имени Блеза Паскаля (1623-1662) в трудах которого она встречается. Это название исторически неточно, т. к. такую таблицу знал уже арабский математик и поэт Омар Хайям, живший в XIII в.

Для любых чисел

Используя метод математической индукции можно доказать, что для любого натурального верно:

Это равенство принято называть биномом Ньютона.

Свойства разложения бинома:

1. Число всех членов разложения на единицу больше показателя степени бинома, т. е. равно .

2. Сумма показателей степеней и каждого члена разложения равна показателю степени бинома, т. е. .

3. Общий член разложения (обозначим его 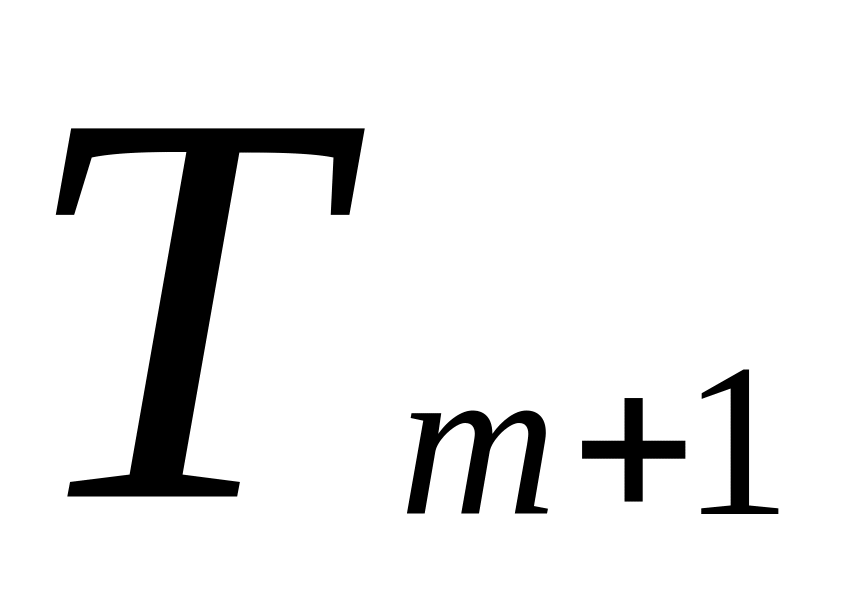) имеет вид =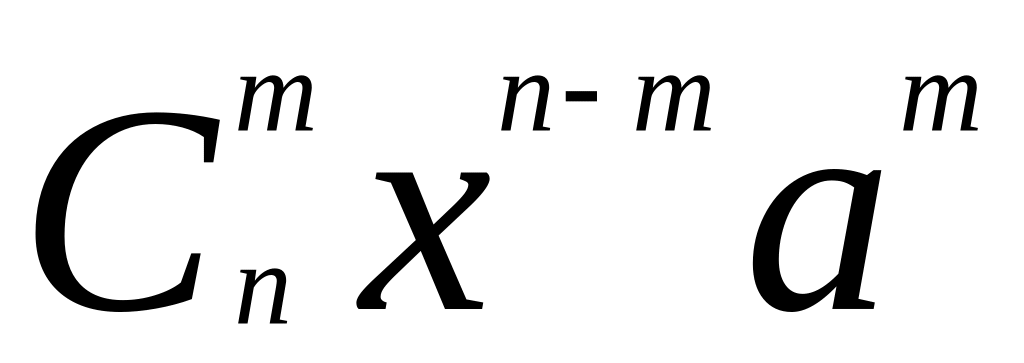 , , 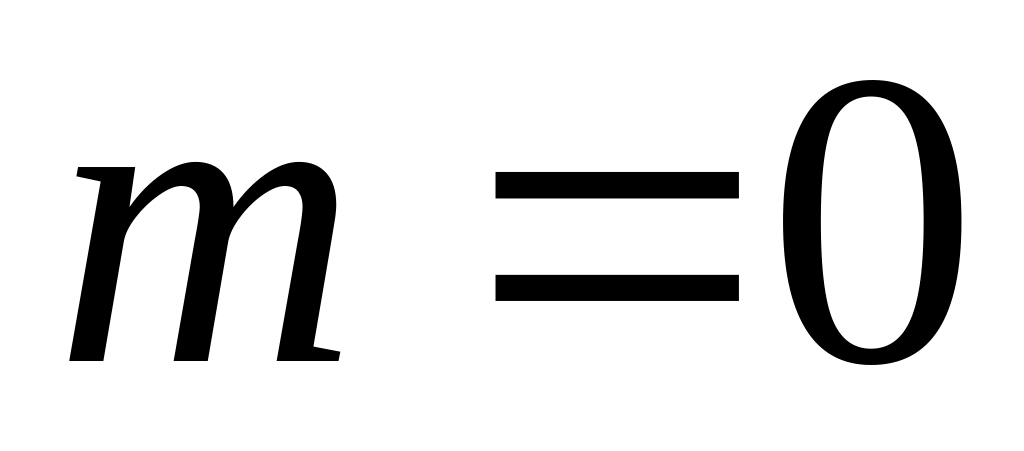1, , .

При этом Т обозначает член разложения, а индекс – его порядковый номер в разложении бинома, считая слева направо.

Например, найдем шестой член разложения :

4. Биноминальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой, т. к. =

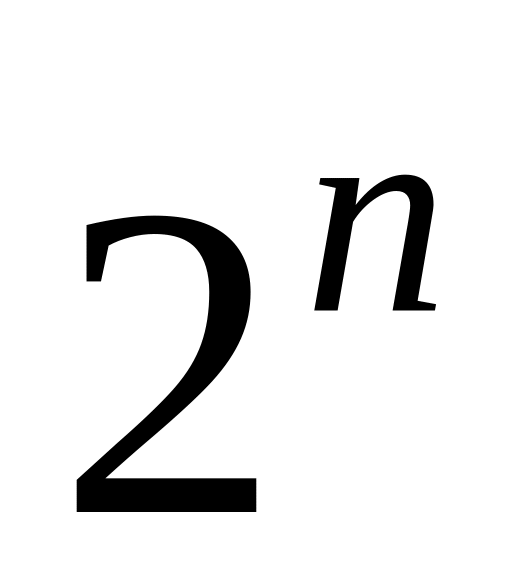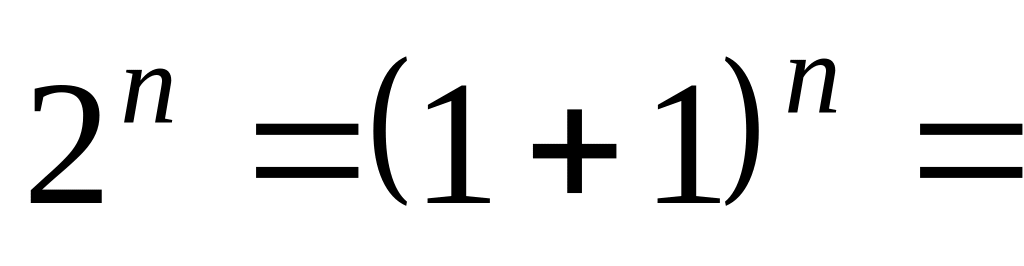
5. Сумма биномиальных коэффициентов равна , т. к. (по биному Ньютона при и ).

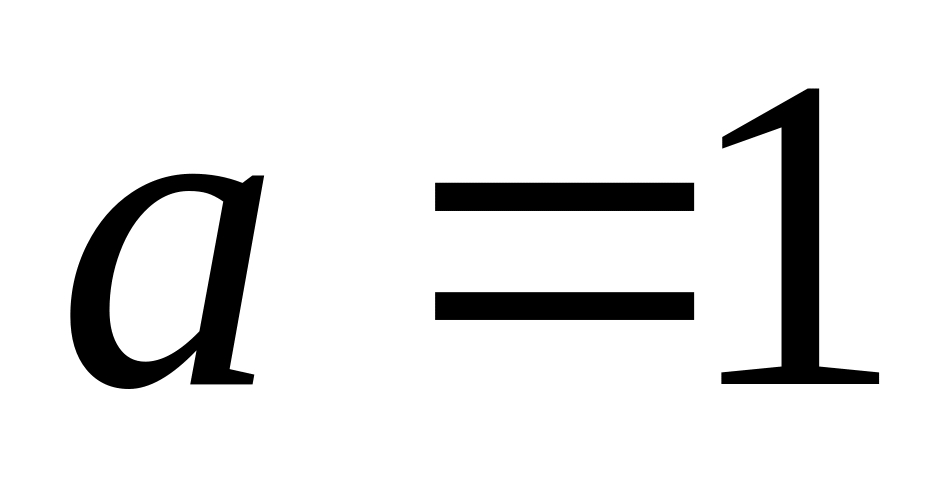До сих пор мы рассматривали соединения, в каждое из которых любой из различных элементов входит только один раз. Можно же рассматривать соединения с повторениями, т. е. соединения, в каждом из которых любой из различных элементов может входить более одного раза. Размещения из элементов, в каждое из которых входит элементов, причем один и тот же элемент может повторятся в каждом размещении любое число раз, но не более , называется размещением из элементов по с повторениями. Их число обозначим и .

Например, размещения из двух элементов по повторениями имеют вид: , , , , , , , . Их количество .

Перестановки из n элементов, в каждую из которых входят одинаковых элементов одного типа, одинаковых элементов другого типа и т. д. до одинаковых элементов -го типа, где , называются перестановками из элементов с повторениями.

Например, числа 4455, 5544, 5454, 4545, 4554, 5445 являются перестановками цифр 4 и 5, каждая из которых взята по два раза.

Число таких перестановок с повторением принято обозначать и оно может быть найдено по формуле .

Пример. Сколькими способами можно расположить в ряд две зеленые и четыре красные лампочки?

Решение.

(2,4)= способами.

Сочетаниями из предметов по с повторениями называются соединения, содержащие m элементов (без учета порядка следования) причем любой элемент может входить в это соединение несколько раз не больше чем . Например, сочетания из трех цифр 3, 4, 5 по два с повторениями записываются в виде 33, 34, 35, 44, 45, 55 или в виде 33, 43, 53, 44, 54, 55, т. к. соединение 43 и соединение 34 есть одно и то же сочетание.

Число всех таких сочетаний обозначим . При этом = .

Например .