Тема 2. Декартово произведение множеств. Бинарные соответствия и отношения Сведения из теории

Пусть даны два множества и . Например, множество  – множество флаконов духов(10 штук) и множество – книги (100 штук). С помощью множеств и мы можем составить множество подарков (100 штук), состоящих из двух предметов – духи и книга.

Каждый подарок можно назвать парой. Причем, в этом случае не важно, какой из этих предметов первый, а какой второй. Если же мы хотим оформить документально наличие подарков и их содержание, то мы составляем таблицу, в которой содержится наименование подарка и содержание подарка, причем название предметов обычно одинаковое. Например, первым идет название книги, вторым название духов. Итак, мы теперь говорим о паре, в которой существует порядок следования компонент: на первом месте название книги, на втором – название духов. В этом случае говорят об упорядоченной паре.

Пусть теперь даны произвольные множества и (не пустые). Мы можем говорить об упорядоченных парах элементов множеств и таких, у которых первая компонента берется из множества , а вторая из множества . Такие пары мы будем обозначать символом , причем , . На первую компоненту не накладывается никаких ограничений, кроме принадлежности множеству , на вторую компоненту не накладывается никаких ограничений, кроме принадлежности множеству . Множество упорядоченных пар , где , называют декартовым произведением множеств и и обозначают символом . Другими словами . Аналогично  – декартово произведение трех множеств , и С.  – декартово произведение n множеств , , , . Ясно, если множества и конечны и , , то тоже конечное, причем .

Если хотя бы одно из множеств бесконечно, то декартово произведение тоже бесконечное. В частности, можно говорить о декартовом произведении множества на себя, т. е. о . Декартово произведение множества на себя называют декартовым квадратом множества и обозначают символом . Другими словами, . Например, если , то .

Непустое подмножество декартова произведения множеств и называется бинарным соответствием из множества множество .

Например, если , , то будет бинарным соответствием из множества в множество , т. к. и .

Значит для данных множеств и бинарное соответствие не одно, т. к. непустых подмножеств множества не одно. Сколько непустых подмножеств у множества , столько и различных бинарных соответствий из множества множество .

Если – бинарное соответствие из множества в множество , то А называют множеством исхода, а – множество прибытия данного бинарного соответствия.

Если пары , то элемент из множества называется точкой исхода, а элемент из множества – точкой прибытия в данном бинарном соответствии .

У каждой точки исхода должна быть хотя бы одна точка прибытия. Для каждой точки прибытия должна быть хотя бы одна точка исхода. Итак, не каждый элемент множества обязан быть точкой исхода, и не каждый элемент множества обязан быть точкой прибытия данного бинарного соответствия .

Множество точек исхода данного бинарного соответствия из множества в множество называется проекцией бинарного соответствия на множество и обозначается символом . Множество точек прибытия соответствия называется проекцией бинарного соответствия на множество и обозначается символом .

Итак, ,

, .

В предыдущем примере, , .

Очень часто факт принадлежности пары бинарному соответствию обозначают символом и читают: элемент соответствует элементу у согласно соответствия .

В нашем примере: элементу 1 соответствует элемент и соответствует элемент , элементу 2 нет соответствующего элемента. При этом можно записать: ; ; .

Так как бинарное соответствие есть подмножество множеств , то можно говорить о дополнении множества до множества или до . , поэтому тоже бинарное соответствие из множества множество . Оно называется соответствием противоположным к соответствию .

Итак , если .

Другими словами, , если не . В нашем примере {(1; в), (2; а), (2; в), (2; с), (3; а), (3; в)}. Бинарные соответствия из множества в множество при конеч­ных и можно представить наглядно при помощи графиков и гра­фов.

График бинарного соответствия из множества в множество состоит из точек. Точек на графике столько, сколько пар в . На плоскости строится прямой угол с вершиной в некоторой точке. Обычно одна из сторон угла – горизонтальна, другая – вертикальна. На горизонтальной оси столько точек, сколько элементов в множестве (вершина угла не используется).

П усть . Каждой точке припишем символ элементов множества . Порядок следования символов не существенен, расстояние между точками не обязательно одинаковое. На вертикальной стороне угла отмечаем столько точек, сколько элементов в множестве (не используем вершину угла) Пусть . Каждой точке припишем символ элементов множества . Порядок следования символов не существенен, расстояние между точками не обязательно одинаковые. (рис. 1).

П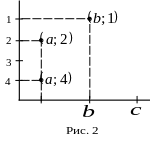 усть . Тогда на горизонтальной стороне находим точку с символом и через нее восстанавливаем вертикаль; на вертикальной стороне находим точку с символом и от нее проводим горизонталь. Точка пересечения проведенных горизонтали и вертикали будет соответствовать паре .

Например, . (рис. 2). График такого бинарного соответствия состоит из трех точек.

Зная график некоторого бинарного соответствия, мы можем записать это соответ­ствие с помощью пар и указать его множества исхода и прибытия.

Например, дан график некоторого бинарного соответствия. (рис. 3). График состоит из четырех точек. Значит бинарное соответствие состоит из 4-х пар. Множество исхода . Множество прибытия . Бинарное соответствие {(2; *), (3; Δ), (4; Δ), (4; О)}.

Г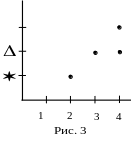 раф бинарного соответствия представляет собой чертеж, состоящий из точек, соединенных стрелками. Для построения графа бинарного соответствиями должны отметить точками все элементы множества и множества (обычно по вертикали параллельно друг другу), приписав этим точкам соответствующие символы.

В предыдущем примере. (рис. 4).

Если , то находим точку с символом и от нее проведем стрелку (обычно по дуге) к элементу с символом . В предыдущем примере. (рис. 5).

Зная граф бинарного соответствия , мы сможем написать это соответствие с помощью пар. Например, дан граф. (рис. 6).

С оответствие  – бинарное соответствие из множества в множество .

Заметим, если множество исхода или множество исхода бесконечны, и бинарное соответствие из множества в множество тоже бесконечно, то можно говорить только о части графа и части графика этого соответствия.

М ожно говорить о бинарном соответствии из множества в это же множество . Такие бинарные соответствия называются бинарными отношениями на множестве . Итак, бинарными отношениями на множестве называется непустое подмножество декартового квадрата множества .

Например, . , т. е. |.

Л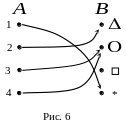 юбое непустое подмножества множества (а таких подмножеств2¹⁶-1) будет бинарным отношением на множестве . Например, . При этом мы можем записать , , , , и т.д. Тогда  – противоположное отношение.

Кроме того вводится понятие обратного отношения : .

Д ругими словами , если : элемент находится в отношении с элементом , если у находится в отношении с элементом . Например, пусть , . Тогда , . Так как бинарное отношение есть частный случай бинарного соответствия, то для него можно говорить и о графике и о графе. Причем, при построении графика никаких особенностей нет, а при построении графа применяют в целях удобства некоторые изменения. Именно, точки, соответствующие элементам множества отмечают по кругу. Например, пусть . (рис. 7). Тогда граф отношения на множестве будет состоять из точек, стрелок и петлей. Например, путь {(1;1),(1;4),(4;1),(5;3),(2;2)}. (рис. 8).

Б инарное отношение на множестве может иметь следующие свойства:

1. Рефлексивность: : .

Другими словами, каждый элемент из множества находится в отношении с самим собой.

Например, – множество людей на Земле. Отношение – “быть другом”, т. е. тогда и только тогда, когда человек друг человека . Это отношение рефлексивно, т. к. каждый человек друг самому себе.

Пусть – множество людей на Земле. Отношение – “быть сыном”, т. е. тогда и только тогда, когда человек сын человека . Это отношение не является рефлексивным, т. к. можно найти человека , который не является сыном самому себе (более того, ни один из людей не является сыном самого себя).

2. Симметричность; .

Другими словами, если элемент из множества находится в отношении с элементом , то и элемент находится в отношении с элементом .

Например: – множество людей на Земле. Отношение – “быть другом”. Это отношение симметрично, т. к. если человек друг человека , то и друг . Отношение – “быть сыном” не является симметричным, т. к. если сын , то не обязан быть сыном (более сильно, не сын )

3. Антисимметричность: и , т. е. и . Примером антисимметричного отношения является отношение «быть сыном» на множестве всех людей на Земле, т. к. сын у влечет за собой – не сын .

4. Транзитивность: , .

Другими словами, если находится в отношении с , а находится в отношении с , то находится в отношении с .

Например, отношение “быть другом” не является тран­зитивным, т. к. из условия друг , а друг , еще не следует, что друг .

Если бинарное отношение на множестве рефлексивно, симметрично, транзитивно, то оно называется эквивалентным.

Например, путь – множество прямых на плоскости. Ведем отношение “параллельность” прямых следующим образом: прямая параллельна прямой тогда и только тогда, когда прямые и не имеют общих точек или совпадают. Тогда отношение “параллельность”:

1) рефлексивно, т. к. любая прямая плоскости параллельна сама себе,

2) симметрично, т. к. если , то ,

3) транзитивно, т. к. если и , то .

При решении конкретных задач часто не удобно работать с элементами множества. Например, мы имеем множество спортсменов в данном клубе. Работать персонально с каждым (оформлять поездки, расписание занятий и т.п.)неудобно. Поэтому часто более удобно работать с группами (классами) элементов данного множества. Явно удобнее работать со спортсменами, распределенными, например, по группам, а в каждой группе распределять спортсменов на подгруппы по мастерству и т.п. Чтобы обобщить такого сорта задачи в теории множеств вводится понятие разбиения множества.

Пусть – непустое множество. И пусть , , , – набор подмножеств множества , обладающий следующими свойствами:

1) ;

2) при ;

3) .

Тогда набор множеств , , , называется разбиением множества .

Например, дано множество – студентов первого курса дневного обучения географического факультета. Мы имеем несколько разбиений этого множества. Например, по специальностям: “геоэкология”, “география”, “картография”. Можно указать и другое разбиение, например, по изучаемым иностранным языкам и т.д.

Если на множестве задано бинарное отношение , являющееся эквивалентностью, т. е. рефлексивно, симметрично, транзитивно, то можно создать разбиение множества по отношению эквивалентности :

1 шаг. Возьмем из какой-нибудь элемент, например . Соберем в один класс все элементы из множества , находящиеся в отношении с элементом :

.

Если , то разбиение состоит из одного класса.

2 шаг. Если , то : , т. е. . Соберем в один класс все элементы множества , находящиеся в отношении с элементом :

.

Если , то разбиение состоит из двух классов ( и ). Если , то существует элемент , т. е. и . Тогда 3 шаг. Собираем и т.д.

Процесс может быть конечным, может быть бесконечным.

За счет рефлективности, симметричности и транзитивности отношения можно сказать, что:

1) каждый класс не пуст,

2)пересечение дух разных классов пусто,

3)объединение полученных классов дает множество. Значит, зная некую эквивалентность на данном множестве всегда можно иметь разбиение этого множества по данной эквивалентности. Верно и обратное. Если на множестве задано некоторое разбиение, то среди всех возможных эквивалентностей на множестве можно найти такую, которая задает именно данное разбиение. Другими словами разбиение множества и эквивалентности на этом множестве задают друг друга. Кроме отношения эквивалентности, большую роль играют отношения, называемые отношениями порядка.

Бинарное отношение на множестве называется отношением порядка, если оно транзитивно и антисимметрично. Множество на котором задано отношение порядка, называется упорядоченным множеством.

Не следует думать, что все отношения подразделяются только на отношения эквивалентности и отношения порядка. Существует огромное число отношений, не являющихся ни отношением эквивалентности, ни отношением порядка, но играющих важную роль в решении различных задач.