МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Утверждена на заседании кафедры ИСС 26 апреля 2011 г.

Методические указания

к практическим занятиям

по курсу «Высшая математика»

Раздел «Линейная и векторная алгебра»

для бакалавров дневной формы обучения

института ПГС

Ростов-на-Дону

2011

УДК 512.8 (08)

Методические указания к практическим занятиям по курсу «Высшая математика». Раздел «Линейная и векторная алгебра».– Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 20 c.

Изложен теоретический и практический материал по линейной, векторной алгебре и элементам аналитической геометрии.

Предназначены для бакалавров дневной формы обучения специальностей института ПГС.

Электронная версия находится в библиотеке, ауд. 224.

УДК 512.8 (08)

Составители:

канд. физ.-мат. наук, доц. А.Е. Богданов

канд. техн. наук, доц. Г.Я. Корабельников

ассист. Неумержицкая Н.В.

Рецензент:

д-р физ.-мат. наук, проф. А.А. Ляпин

Редактор Н.Е. Гладких

Доп. план 2011 г., поз. 17

Подписано в печать 18.07.11. Формат 60х84/16.

Бумага белая. Ризограф. Уч.-изд. л. 1,0. Тираж 20 экз. Заказ 224

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов - на - Дону, ул. Социалистическая, 162

 РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ

СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2011

Линейная алгебра Системы линейных уравнений

Выражение вида

называется линейной системой из m уравнений и n неизвестных .

Решением системы называется такая система n чисел , когда каждое уравнение системы обращается в тождество после замены в нем неизвестных соответствующими числами

Система линейных уравнений может не иметь ни одного решения, и тогда она называется несовместной.

Если же система линейных уравнений обладает решениями, то она называется совместной.

Совместная система называется определенной, если она обладает одним- единственным решением, и неопределенной , если решений больше одного .

Пусть дана система двух линейных уравнений с двумя неизвестными .

Определителем 2-го порядка (определителем системы) называется число :

.

Пусть дана система трех линейных уравнений с тремя неизвестными

.

Определителем 3-го порядка(определителем системы) называется число

.

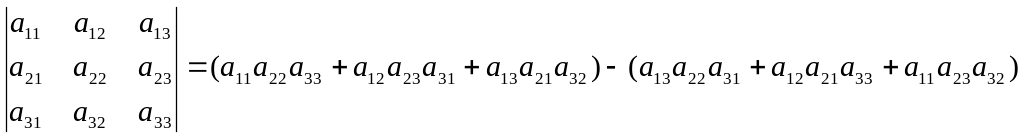Пусть дана система n линейных уравнений с n неизвестными

.

Определителем n-го порядка(определителем системы) называется число

.

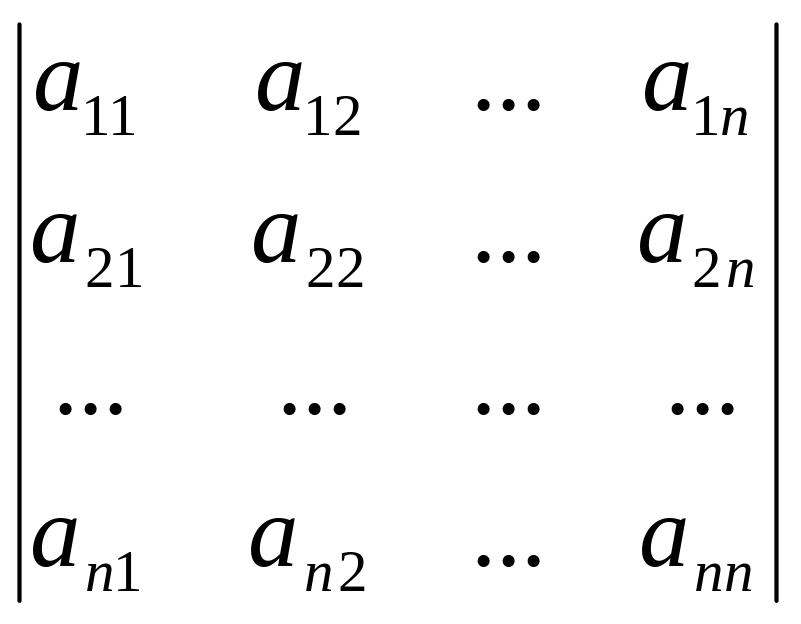Пусть дан определитель n-го порядка

.

Определитель (n-1)-го порядка, получающийся вычеркиванием из данного определителя -й строки и -го столбца, называется минором элемента и будем его обозначать .

назовем алгебраическим дополнением элемента .

Определитель равен сумме произведений всех элементов произвольной строки или столбца на их алгебраические дополнения .

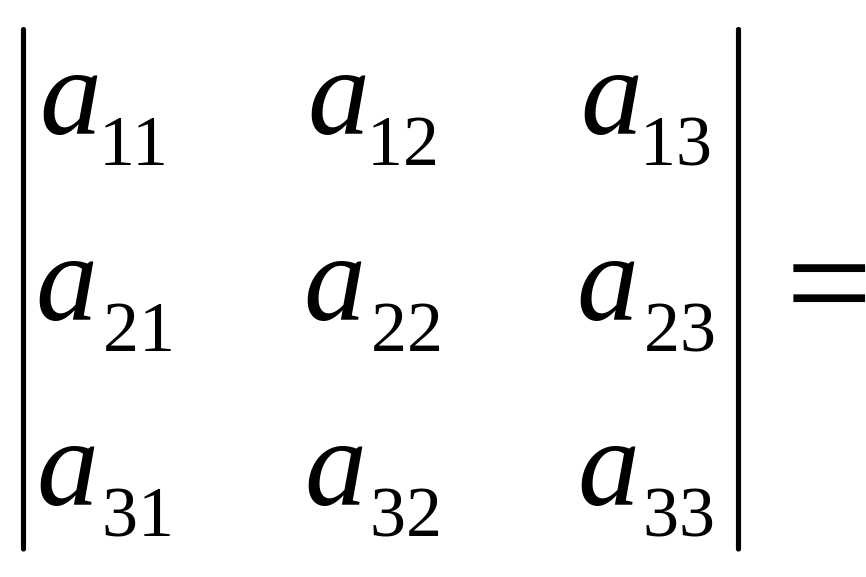
= = и т.д.

Правило Крамера. Пусть дана система n линейных уравнений с n неизвестными

.

Если определитель системы отличен от нуля , то система имеет единственное решение при любой правой части и это решение получается по формулам :

где , , … , .

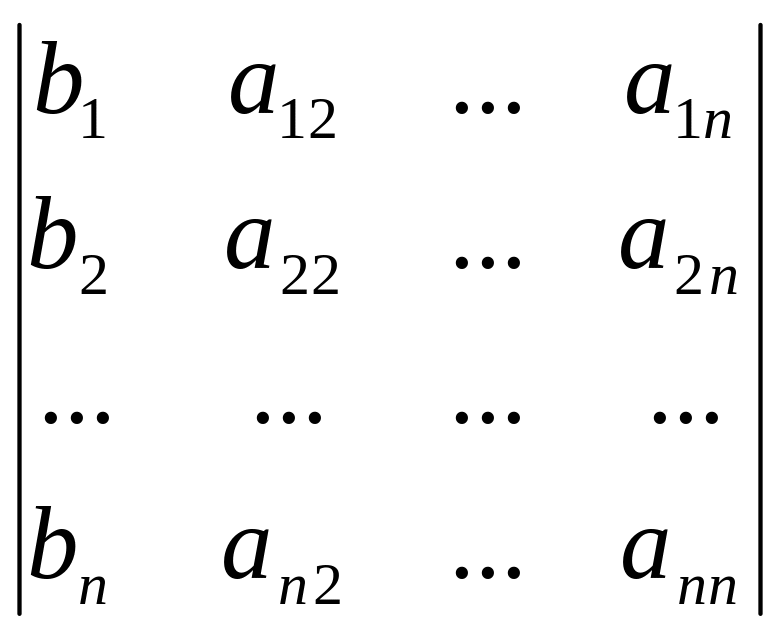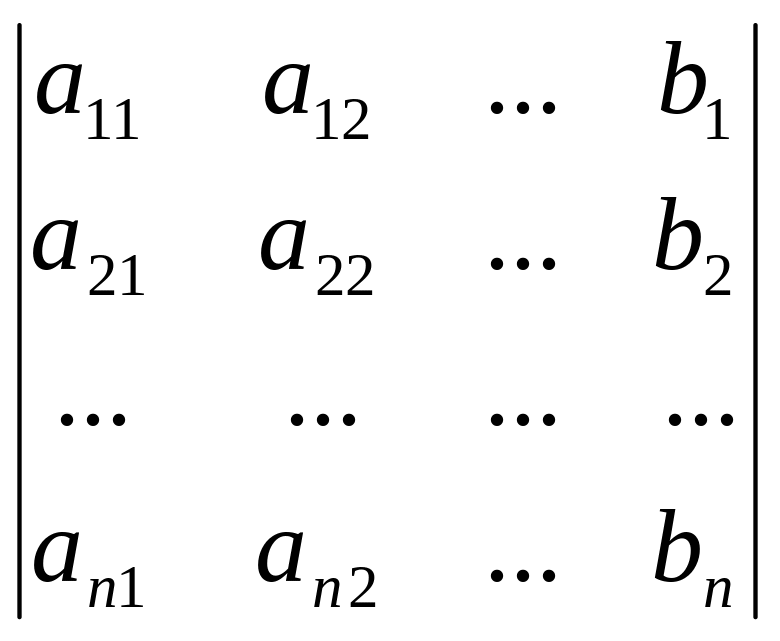Решение систем уравнений методом Крамера

1.

Определитель системы .

Вспомогательные определители

, .

Решение системы

2.

Определитель системы вычислим по формуле (4)

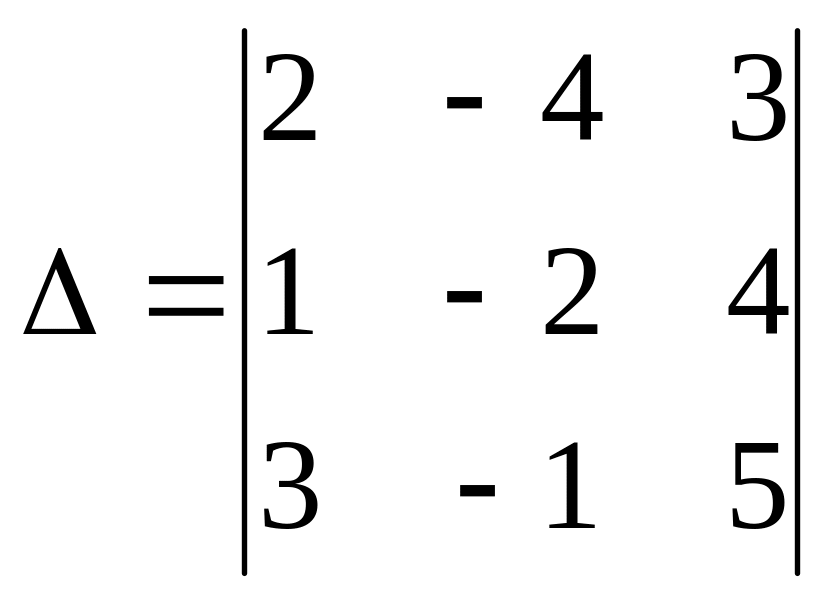= 2(-2)5+1(-1)3+3(-4)4 – ( 3(-2)3+2(-1)4+5(-4)1 ) =-25

Вспомогательный определитель вычислим разложением по элементам первой строки

= ,

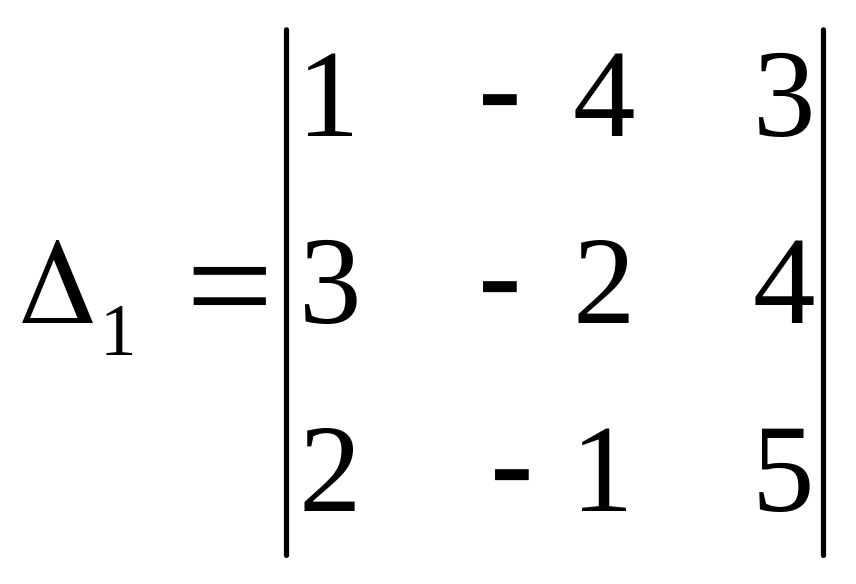определитель вычислим разложением по элементам первого столбца

,

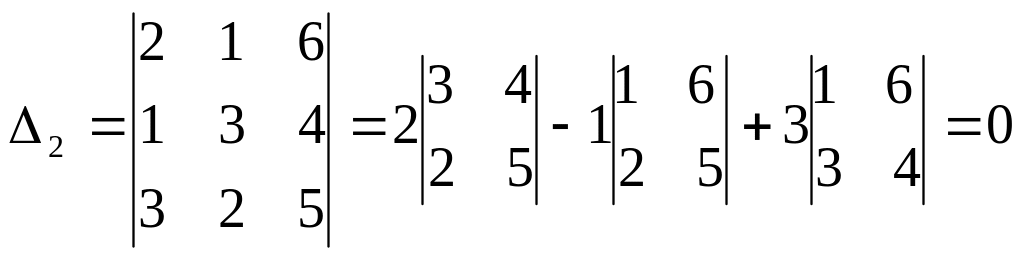определитель вычислим разложением по элементам третьей строки

.

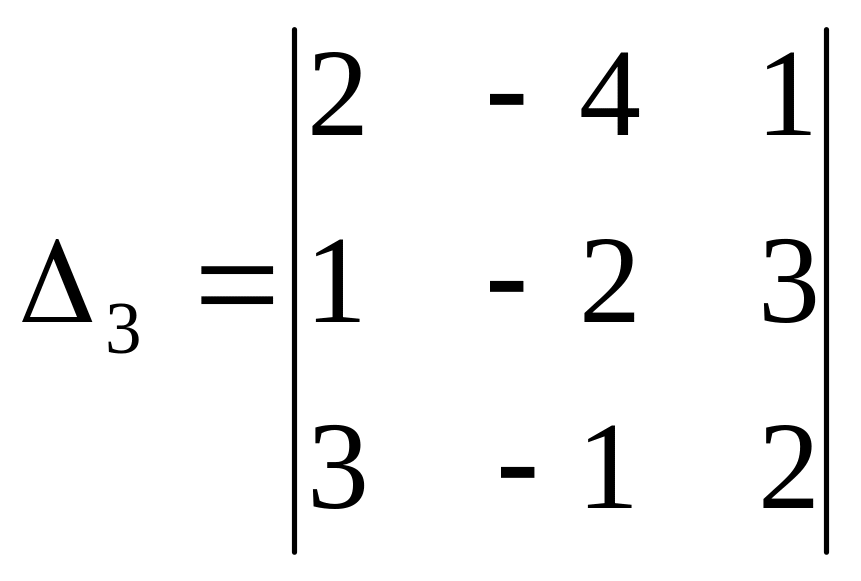
Пусть дана линейная система

.

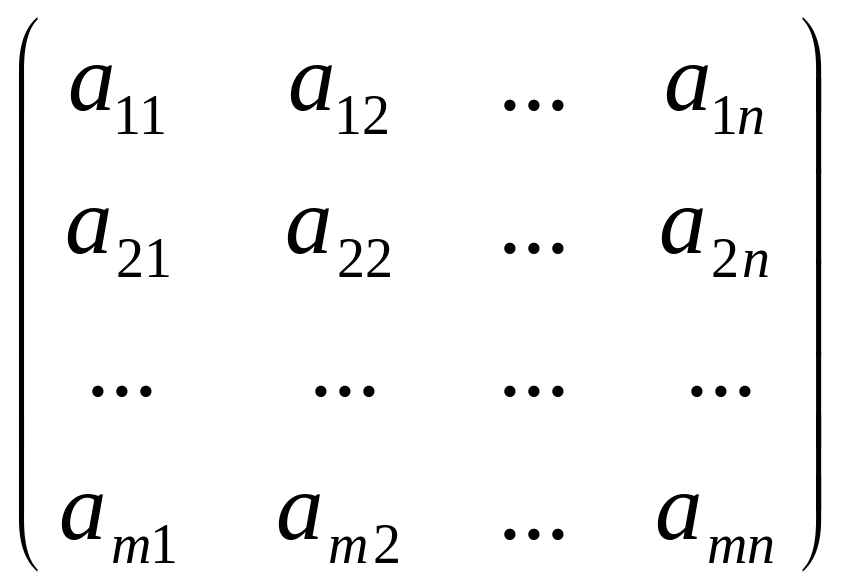Таблица из элементов называется матрицей из строк и столбцов ;

числа называются элементами матрицы .

Если , то матрица называется квадратной порядка .

Диагональ этой матрицы , составленная из элементов , называется главной диагональю .

Квадратная матрица порядка будет называться единичной матрицей порядка , если все элементы ее главной диагонали равны единице , а все остальные равны нулю .

Пусть дана матрица,

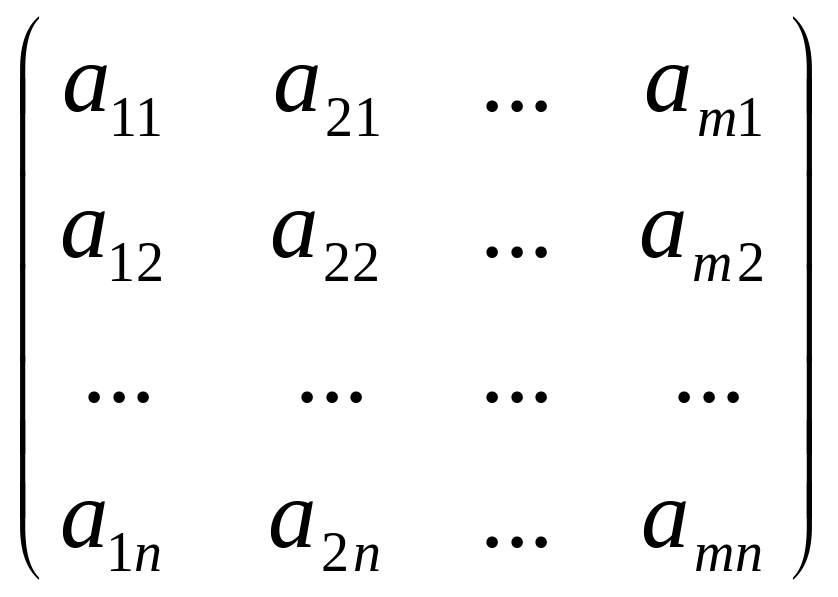
А = . Матрица А^Т = называется транспонированной матрицей матрицы А .

Операции над матрицами

Суммой А + В двух матриц А = ( ) и В = ( ) размерности называется матрица С = ( ) такая , что .

Произведением kА матрицы А = ( ) на число k называется матрица

В = ( ) такая , что k .

Произведением матрицы А = ( ) размерности на матрицу В = ( ) размерности называется матрица С = АВ = ( ) размерности такая , что .

Пусть дана квадратная матрица

А = 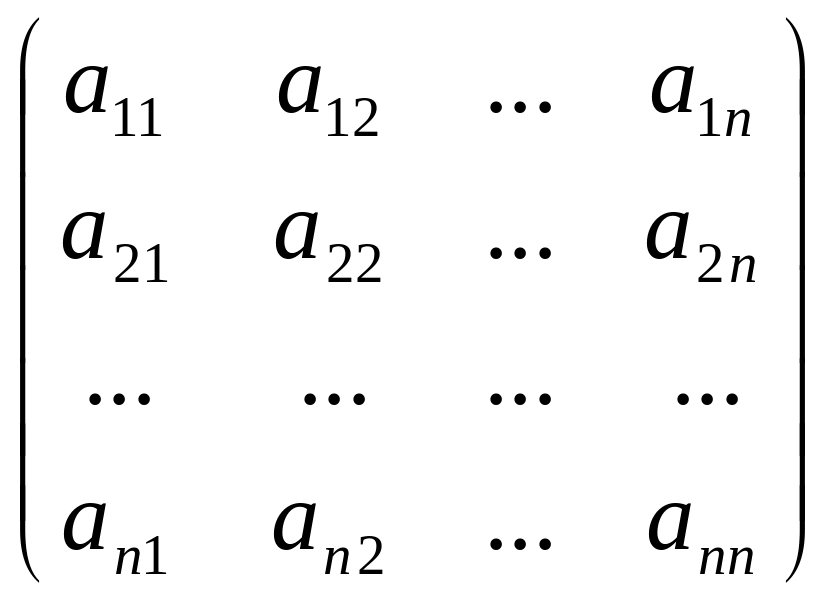и ее определитель А .

Если определитель квадратной матрицы равен нулю, то матрица называется вырожденной ( особенной ) , и невырожденной (неособенной) – в противоположном случае .

Матрица В называется обратной для матрицы А, если АВ = ВА = Е и будем ее обозначать В = А^-1 .

Для невырожденной матрицы А существует обратная матрица, причем единственная и

А^-1 = .

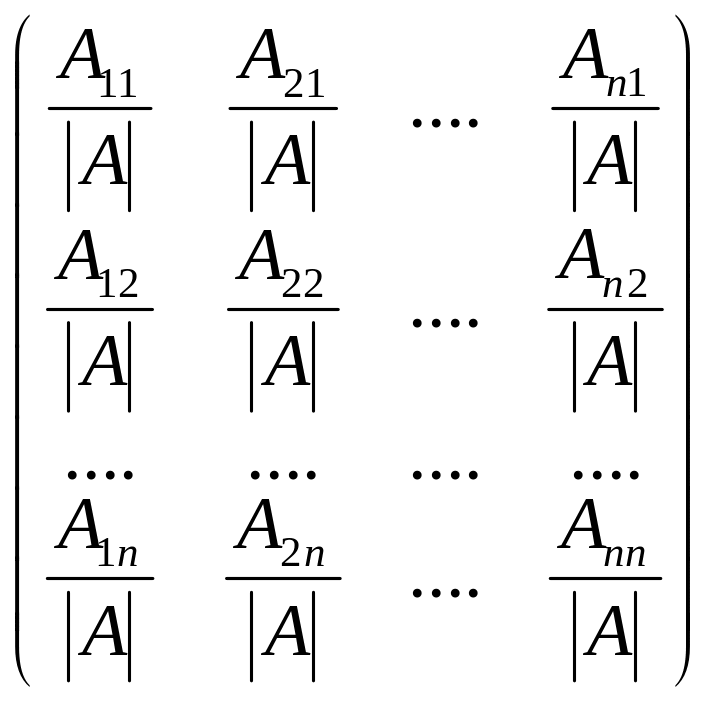Примеры

1. .

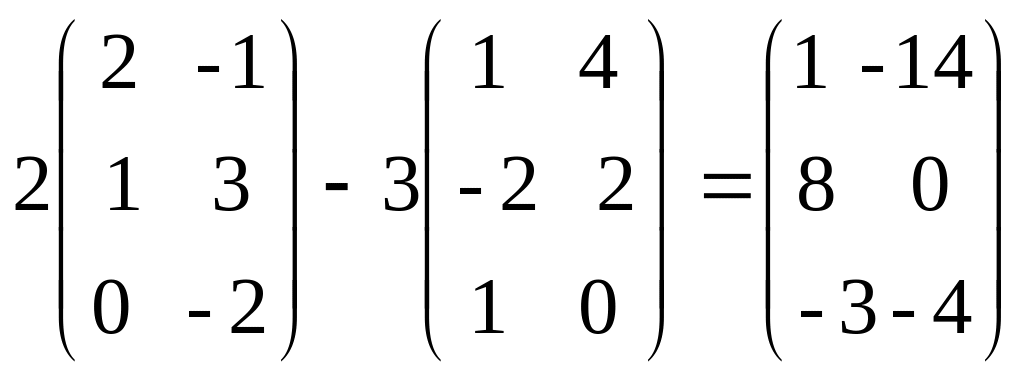2.

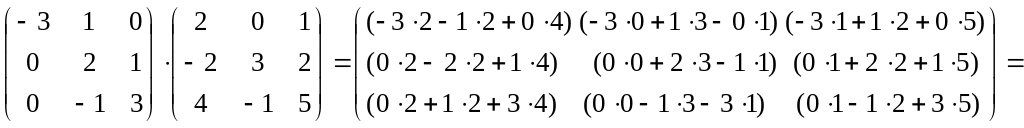
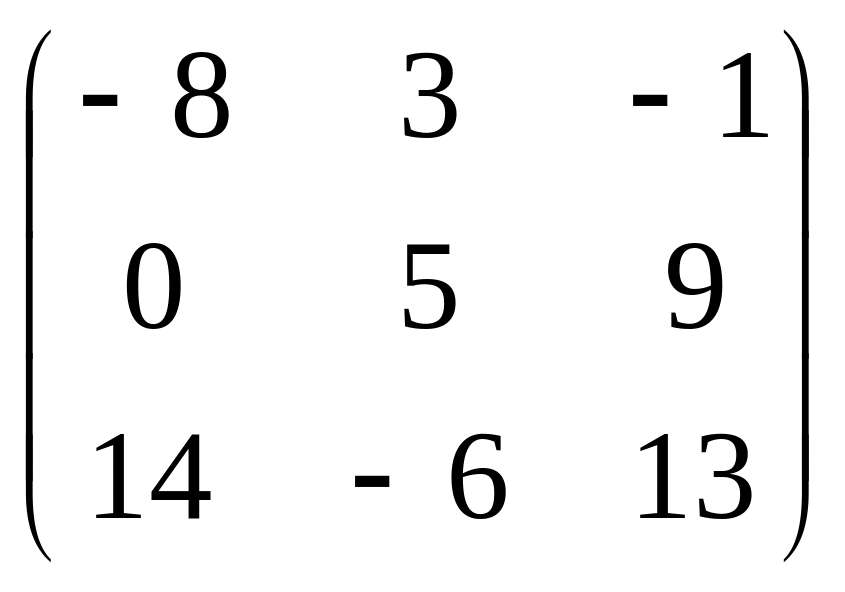
3. Дана матрица = 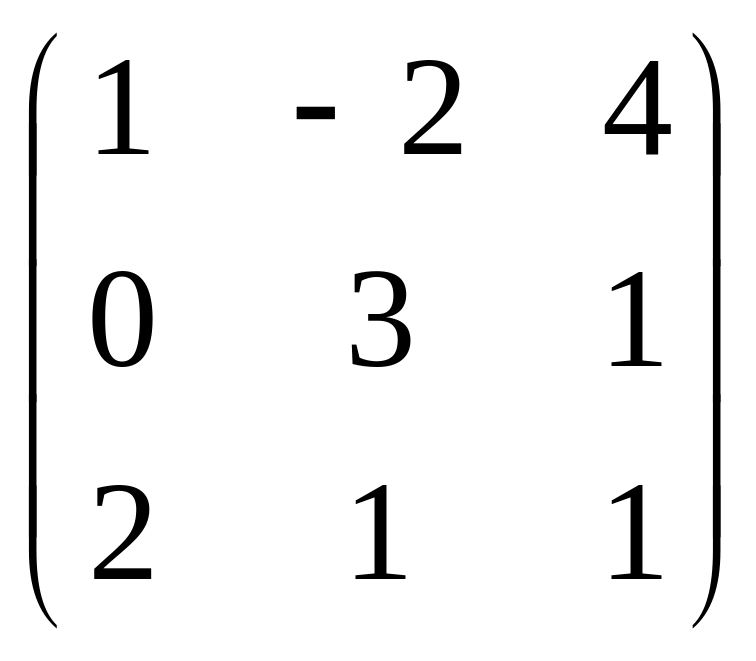, найти обратную.

,

, , = ,

, , .

.

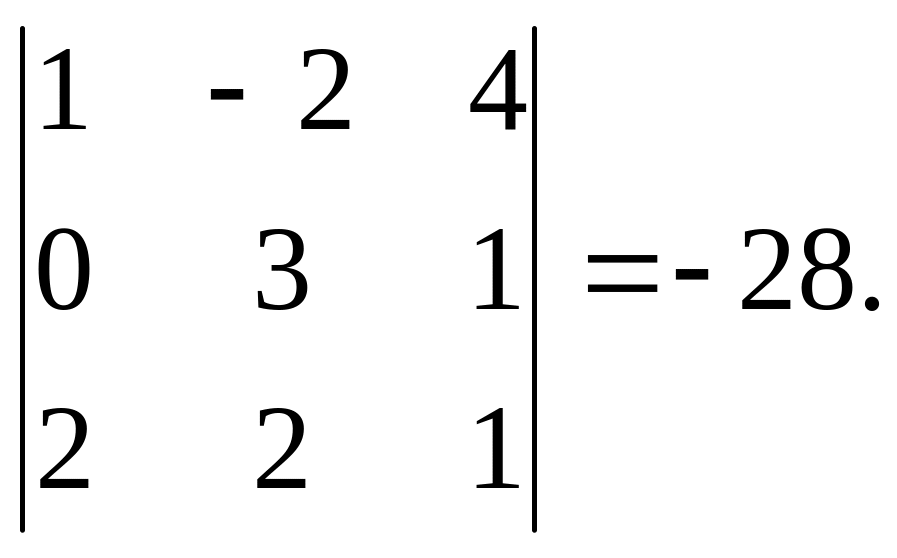
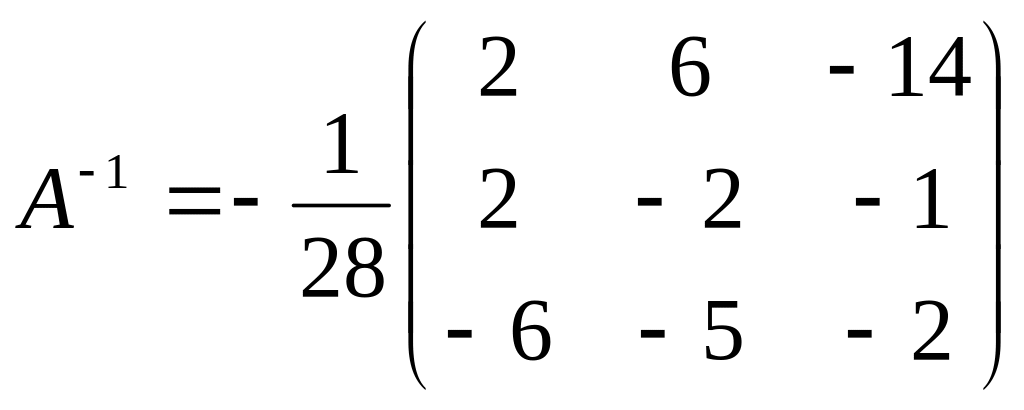Матричный способ решения систем линейных уравнений

Пусть дана система n линейных уравнений с n неизвестными

.

А = - матрица системы , через в = и Х = , тогда исходную систему можно записать в матричной форме АХ = в (*) .

Если определитель системы отличен от нуля , то ее решение находится следующим образом

= . .

Решить систему уравнений матричным способом

1.

Cоставим матрицу системы

и вычислим определитель матрицы .

Найдем алгебраические дополнения

Получаем обратную матрицу , тогда

,

2.

Составим матрицу системы

и вычислим определитель матрицы .

Найдем алгебраические дополнения

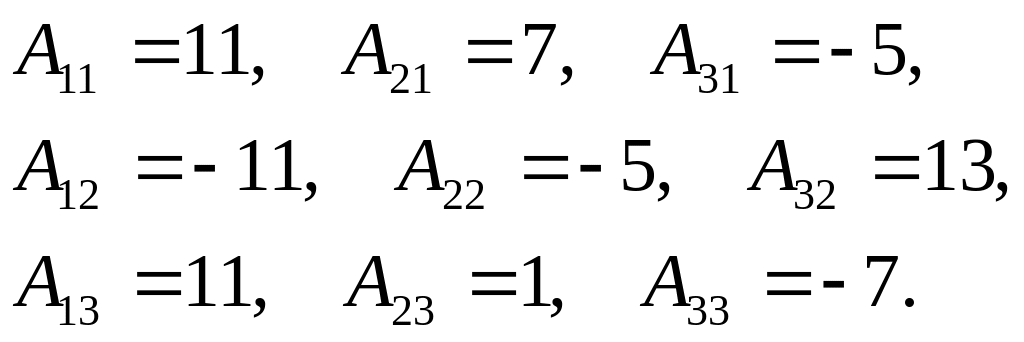
Получаем обратную матрицу .

Тогда ,

Линейное векторное пространство

Упорядоченная система из n чисел  = ( ) называется n - мерным вектором, а числа называются компонентами вектора  .

Векторы  = ( ) и  = ( ) будут считаться равными , если .

Суммой векторов  и  называется вектор  +  = ( ) .

Вектор 0 = ( 0,0,…,0) называется нулевым .

Вектором, противоположным вектору , назовем вектор - =( ).

Произведением вектора  на число k называется вектор k = ( ) .

Вектор  называется линейной комбинацией векторов ₁, ₂, …, _s, если существуют такие числа р₁ , р₂ , … , р_s , что  = р₁₁+ р₂₂ + … + р_s_s .

Система векторов ₁ , ₂ , … , _s линейно зависима , если существуют такие числа р₁ , р₂ , … , р_s , хотя бы одно из которых отлично от нуля , когда имеет место равенство р₁₁+ р₂₂ + … + р_s_s = 0 , в противном случаи система линейно зависима.

Система из n векторов образует базис линейного n - мерного пространства , если они линейно независимые и любой другой вектор линейного пространства является их линейной комбинацией .

Система векторов ₁=(1, 0, … , 0), ₂=(0, 1, … , 0), … , _n=(0, 0, …, 1), которые называются единичными, образует базис n - мерного векторного пространства .

Доказать, что система векторов образует базис в R³, и найти координаты вектора в этом базисе .

Рассмотрим равенство . Оно эквивалентно следующей линейной однородной системе :

, т.к. определитель системы ,

то система имеет только нулевое решение и , следовательно , векторы

- линейно независимые .

Теперь покажем, что любой вектор из R³ можно представить в виде их линейной комбинации, т.е. , и тем самым докажем , что векторы образуют базис в R³ , а есть координаты вектора в новом базисе .

Действительно записанное ранее векторное равенство эквивалентно следующей линейной системе:

. Так как определитель системы , то, по правилу Крамера, система имеет решение при любой правой части, а это означает, что любой вектор из R³ можно выразить через векторы , т.е эти векторы образуют базис .

Теперь найдем координаты вектора в этом базисе, для чего запишем систему : . Решая ее, получим

Следовательно, в новом базисе вектор имеет координаты .

Пусть дана матрица А = .

Строки матрицы можно рассматривать как n - мерные векторы, которые могут быть линейно зависимые.

Максимальное число линейно независимых строк матрицы А называется рангом этой матрицы.

Пусть дана система линейных уравнений

и ее матрица А = .

Построим так называемую “расширенную” матрицу,

= .

Система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы равен рангу матрицы А .

Совместная система тогда и только тогда обладает единственным решением, когда ранг матрицы А равен числу неизвестных.

Решения систем линейных уравнений методом Гаусса

П ример 1

Следовательно, система имеет единственное решение.

Найдем решение системы:

Следовательно, система имеет бесконечное множество решений, каждое из которых может быть найдено по формулам:

,

г

Пример 2

де численные значения z задаются произвольно.

Пример 3

Следовательно, система несовместна.