Описание прибора

Рычажные скобы относятся к рычажно-зубчатым приборам повышенной точности и предназначены для относительных измерений методом замещения деталей 5, 6, 7 и 8 квалитетов точности. Рычажная скоба (рис. 1) состоит из корпуса 1, подвижной пятки 10, передвижной (переставной) пятки 9, предохранительного колпачка 7, стопора 8, арретира 2, шкалы 4, указывающей стрелки 5, указателей предельных отклонений 3 и механизма перевода указателей, закрывающегося крышкой 6.

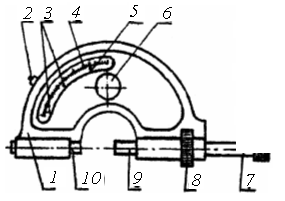
Рис. 1. Рычажная скоба

Правила настройки рычажной скобы следующие:

1. Плитки должны быть чистыми (протирать допускается спиртом или спиртоацетоновой смесью, которыми смачивают ватный тампон).

2. Блок плиток для настройки рычажной скобы составляется из наименьшего числа плиток и не более пяти. Например, размер 17,745 мм можно составить из четырех плиток: 1,005+1,74+5+10=17,745 мм.

3. Составляют блок, надвигая одну плитку на другую. За счет сил молекулярного взаимодействия плитки легко удерживаются в блоке.

4. Отвинчивают предохранительный колпачок 7 и отпускают стопор 8.

5. Вводят блок плиток между пятками 9 и 10 прибора и, вращая стрелку 5 с нулем шкалы 4.

6. Закрепляют стопор 8 и, придерживая блок плиток рукой, несколько раз нажимают на арретир 2. Если при этом стрелка не возвратится в нулевое положение, то вновь произвести настройку.

7. Нажимают на арретир 2, вынимают блок и разбирают его, которые размещают в карманы ящика набора концевых мер.

Проведение измерений и обработка результатов

1. Составить блок концевых мер на требуемый размер с точностью до 0,005 мм (0 или 5 в третьем знаке после запятой).

2. Ознакомиться со схемой измерений, которая представлена на рис. 2.

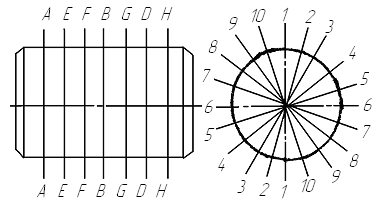
Рис. 2. Схема измерений: А-А; Б-Б; В-В; Г-Г;

Д-Д; Е-Е; F-F – сечения; 1÷1….10÷10 – направления в сечении

Измерения проводят в семи сечениях, в 10 направлениях, равномерно распределенных по окружности детали.

При измерениях в крайних сечениях (А-А и Б-Б) кромка торца валика должен выступать из пор пяток, так как здесь возможные неровности исказят действительный результат (цена деления инструмента составляет 0,002 мм).

Использование данной схемы обеспечивает получение массива данных из 70 результатов измерений.

3. Сформировать массив результатов измерений.

По приведенной в данной работе схеме измерения получают в виде массива данных результаты измерений в количестве n = 70.

Начинают с определения значений и и определение диапазона разброса измерений:

Полученный диапазон должен быть разбит на 10÷15 интервалов. Например: = 11,923 мм; = 11,828 мм; = = 11,923 – 11,898 = 0,025 мм = 25 мкм. Здесь его удобно разбить на 13 интервалов по 2 мкм шириной. Если первый интервал принять равным 11,898÷11,900, то последний тринадцатый будет равен 11,922÷11,924, соответственно середина 1^-го интервала будет равна 11,899, а 13^-го – 11,923 мм.

Далее определить частоты результатов измерения, относящихся к каждому интервалу, при этом следует выполнять, правило: результаты, совпадающие с левой границей интервала включаются в этот интервал, а результаты, попадающие в правую границу интервала, включаются в следующий интервал.

Распределение массива данных по интервалам следует представить в виде табл. 1.

Таблица 1

Номер интер-вала	Интервалы размеров, мм	Среднее значение интервала , мм	Частота результатов mi	Плотность частоты mi/n	mixi	mixi2
1 2 .. 13

4. Построить полигон и гистограмму по результатам измерений.

5. Определить среднее значение, стандартное отклонение и доверительный интервал для среднего значения

Среднее значение определяют по формуле

.

Стандартное отклонение определяют по формуле

.

Доверительный интервал для среднего определяют по формуле

,

где - квантиль для соответствующей вероятности.

Для доверительной вероятности Р = 95 %, = 1,96;

Для доверительной вероятности Р = 99 %, = 2,58;

Для доверительной вероятности Р = 99,73 %, = 3.

Результат измерения записывается в форме: .

6. Проверить гипотезу о равномерном распределении исходных данных.

Уровень значимости принять равным α = 0,05 (доверительный вероятностью Р = 0,95).

Проверка гипотезы о законе неизвестного распределения проводится так же, как и проверка гипотезы о параметрах распределения, при помощи специально подобранной случайной величины – критерия согласия. Под ним понимаем критерий проверки гипотезы о предлагаемом законе неизвестного распределения. Наиболее часто принимают критерий согласия К. Пирсона (Хи - квадрат) как для нормального распределения, так и для других (равномерного, экспоненциального, биноминального, Пуассона и других).

С этой целью сравнивают эмпирические (наблюдаемые) и теоретические (вычисленные) частоты. Теоретические и эмпирические частоты обычно различаются. Это расхождение может быть незначительным и объясняться малым числом наблюдений, способом их группирования либо другими причинами. В другом случае расхождение может быть значимым и объясняться принятием неверной гипотезы о распределении. Критерий К. Пирсона, как и любой другой, не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости (α) ее согласие или несогласие с данными наблюдений. Величина называется уровнем доверия или доверительной вероятностью.

Критерий К. Пирсона определяют по формуле

,

где К – число интервалов;

- частота i-го интервала;

- число испытаний;

- теоретическая вероятность попадания случайной величины в i–й интервал;

_i - теоретическое число попаданий случайной величины (теоретическая частота) в i-й интервал.

Гипотеза о законе распределения принимается, если выполняется условие:

² < ²_кр,

где ²_кр определяется по таблице для принятого значения и числа степеней свободы .

=K-1-S,

где S – число параметров закона распределения, вычисленных по выборке результатов измерений.

Для нормального распределения S = 2, так как функция плотности распределения зависит от двух параметров – α и σ :

.

Как известно или ;

или (точечная оценка стандартного среднеквадратичного отклонения).

Для экспоненциального распределения S = 1, так как функция плотности распределения для экспоненциального распределения. Зависит от одного параметра –λ: . Как известно M( или , отсюда .

Для равномерного распределения S = 2, так как функция плотности распределения зависит от двух параметров α и b:

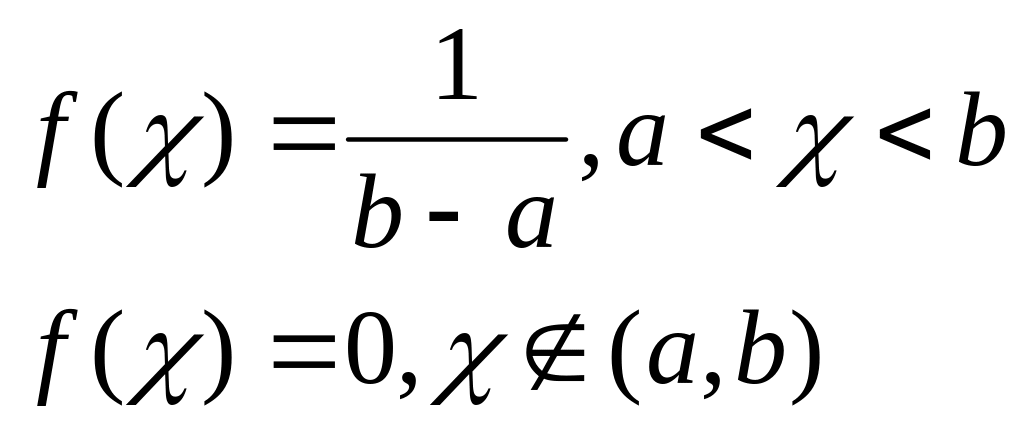
Как известно σ( ) ,

отсюда можно принять ;

(точечная оценка стандартного (среднеквадратичного) отклонения).

6.1. Проверка гипотезы о нормальном распределении

Находят среднеарифметическое значение (выборочное среднее) :

,

где n_i - число результатов в каждом из интервалов;

- среднее значение интервала;

i - номер интервала.

Вычисляют среднеквадратичное отклонение S_x:

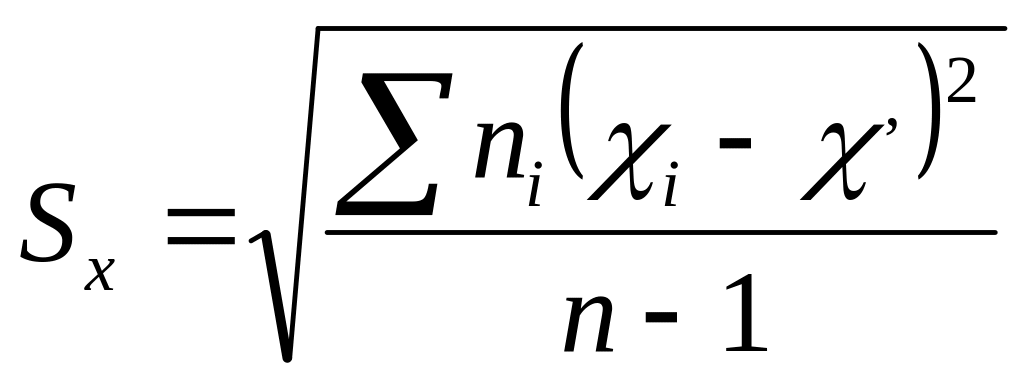
Определяют аргумент z по формуле

,

где z – нормированное значение случайной величины.

6.2. По приложению табл. 1 для φ(z) или φ( ) для каждого интервала определяется плотность нормированного распределения.

Определяют теоретическую частоту m_m попадания результата в каждый интервал по формуле

,

где n – общее число результатов в выборке;

c – ширина интервала;

- среднеквадратичное отклонение.

Для каждого интервала определяется значение по формуле

Определяется значение критерия Пирсона по формуле

,

где - число интервалов после объединения тех интервалов (как правило, крайних), n_i > S.

По приложению табл. 2 находят _крит в зависимости от уровня значимости q (0,05; 0,025) и числа степеней свободы K, которые определяют по формуле

K = z – 3

Делают заключение о принятии гипотезы предполагаемого закона распределения по отклонению:

² < _крит.

Оформление расчета проверки гипотезы о нормальном распределении рекомендуется представить в виде табл. 2.

Таблица 2

№ интервала	Середина интервала	Частота результата ni		φ( )
1 2 3 .
K(r)

6.3. Проверка гипотезы о равномерном законе распределения.

Находят среднеарифметическое (выборочное) значение :

,

где a - наименьшее значение результата;

b - наибольшее значение результата.

Вычисляют среднеквадратичное отклонение результата по формуле

.

Находят теоретическую вероятность p_i для каждого интервала по формуле

,

где c - ширина каждого интервала.

Следует иметь в виду, что все теоретические плотности для каждого интервала одинаковы, а их сумма для всех интервалов должна быть равна .

Определяют теоретическую частоту попадания результата в каждый интервал по формуле

,

где n – общее число результатов (объем выборки).

Для всех интервалов m_i будет одной и той же.

Определяется значение для каждого интервала по формуле

.

Определяем значение критерия Пирсона по формуле

,

где K – число интервалов.

По приложению табл. 2 находят _крит в зависимости от уровня значимости q (0,05 или 0,025) и числа степеней свободы r, которое определяют как r = k - 1.

Делают заключение о принятии гипотезы предполагаемого закона распределения по отношению

² < _крит.

Оформление расчета проверки гипотезы о равномерном распределении представить в виде табл. 3.

Таблица 3

Номер интер- вала	Середи- на интервала,	Частота результата в интервале, ni	Вероят- ность, pi	Теоретическая частота, mi	Критерий
1 2 . 13