2. Формулы для определения вероятностей: а) попадания нормально распределенной случайной величины в заданный интервал; б) ее отклонения от математического ожидания. Правило трех сигм

Рассмотрим свойства случайной величины, распределенной по нормальному закону:

1. Вероятность попадания случайной величины X, распределенной по нормальному закону, в промежуток [x₁; x₂] равна

, где , .

Доказательство.

.

2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания a не превысит величину >0 (по абсолютной величине), равна

, где .

Доказательство.

.

Следствие. Вычислим по этой формуле вероятности при некоторых значениях :

=

=2

=3

Отсюда вытекает правило трех сигм:

Если случайная величина имеет нормальный закон распределения с параметрами a и ² , то практически достоверно, что ее значения заключены в интервале (a-3;a+3) .

3. Центральная предельная теорема. Понятие о теореме Ляпунова

Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Важнейшее место среди них занимает теорема Ляпунова.

Теорема Ляпунова. Если Х₁, Х₂, … , Х_n – независимые случайные величины, у каждой из которых существует математическое ожидание M(X_i)=a_i, дисперсия D(X_i)=  _i², абсолютный центральный момент третьего порядка M(X_i-a_i³) = m_i и

,

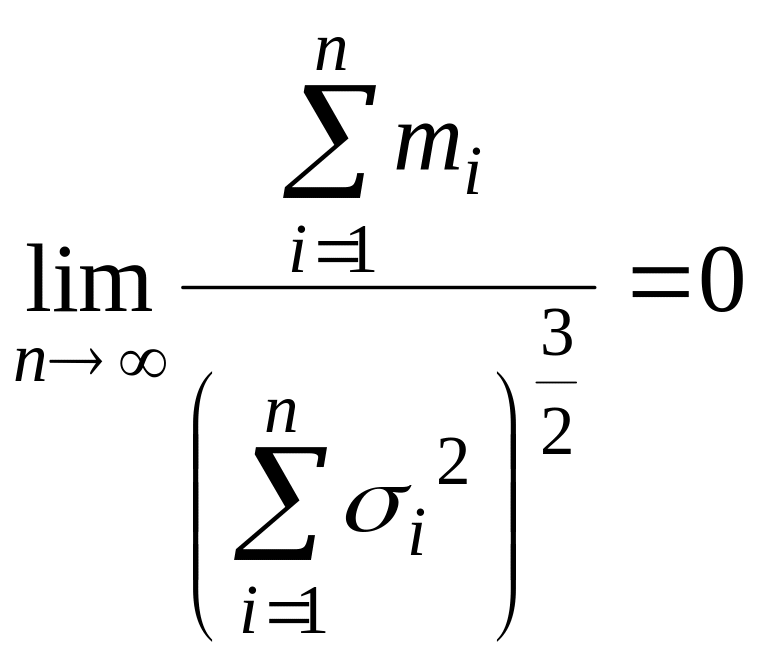то закон распределения суммы Х₁+Х₂+…+Х_n при п неограниченно приближается к нормальному с математическим ожиданием и дисперсией .

Лекция 7 Тема 6: Двумерные (n-мерные) случайные величины

ПЛАН

1. Понятие двумерной (n-мерной) случайные величины.

2. Условные распределения и их нахождение по таблице распределения.

3. Понятие о функции распределения и плотности вероятности двумерной случайной величины.

4. Ковариация и коэффициент корреляции.

1. Понятие двумерной (n-мерной) случайные величины

Ранее мы познакомились со случайными величинами и законами их распределения. Мы рассматривали одномерные случайные величины, которые были разбиты на два большие класса: дискретные и непрерывные.

Дискретная случайная величина считается заданной, если перечислены все её значения Х_i и указаны соответствующие вероятности Р_i, причём, сумма всех вероятностей равна 1, т.е.

Р₁ + … + Р_i + … + Р_n = 1.

Непрерывная случайная величина считается заданной, если известна функция (интегральная функция) её распределения

F(x) = P(X < x),

или плотность распределения её вероятностей, получаемая дифференцированием функции распределения, т.е.

(х) = (х).

Если известна плотность распределения вероятностей непрерывной случайной величины, то интегральная функция её распределения вычисляется по формуле:

F(x) = .

В реальном мире изучаемое явление характеризуется не одной, а несколькими случайными величинами. Такие случайные величины называют многомерными случайными величинами. Приведём примеры таких величин.

Пример 1. Объём продаж квартир на вторичном рынке зависит от многих фактором, а именно, от числа комнат Х₁ в квартире, района города Х₂, типа дома Х₃ и др.

Пример 2. Качество обслуживания судов в порту зависит от количества Х₁ прибывших в порт судов, имеющихся в порту свободных причалов Х₂ и т. д.

Пример 3. Доход инвестора зависит от инвестиционной привлекательности Х₁ ценных бумаг и вложенных в них денежных средств Х₂.

Как видим, многомерные случайные величины характеризуются системой одномерных случайных величин или случайным вектором Х = (Х₁, …, Х_i, …, X_n).

Случайные величины (Х₁, …, Х_i, …, X_n), входящие в систему, могут быть как дискретными (примеры 1 и 2), так и непрерывными (пример 3).

Непрерывные многомерные случайные величины преобразуют в дискретные по тем же правилам, что и для одномерных непрерывных случайных величин.

Изучение многомерных случайных величин проще начать с рассмотрения двумерных случайных величин, так как все полученные выводы легко распространяются на любую систему случайных величин.

Геометрически двумерную случайную величину (Х, У) можно изобразить случайной точкой (вектором) на плоскости.

Исчерпывающим описанием многомерной случайной величины, как и в случае с обычной одномерной случайной величиной, является закон её распределения. Закон распределения дискретной многомерной случайной величины, как и в случае обычной одномерной случайной величины, считается заданным, если перечислены совокупности всех её возможных значений (точек плоскости для двумерной случайной величины) и указаны соответствующие им вероятности.

В общем виде закон распределения двумерной дискретной случайной величины запишем в виде таблицы (матрицы) распределения (таблица 1), в каждой клетке (i,j) которой располагаются вероятности совместного появления соответствующих значений (X_i, Y_j), т.е. P_ij = Р(Х= X_i; У= Y_j).

Таблица 1.

Y j Xi	Y1	…	Yj	…	Ym
Р1	P11	…	P1j	…	P1m	P1
…	…	…	…	…	…	…
Xi	Pi1	…	Pij	…	Pim	Pi
…	…	…	…	…	…	…
Xn	Pn1	…	Pnj	…	Pnm	Pn
	P1	…	Pj	…	Pm	1

Так как в клетках (i,j) таблицы стоят значения (X_i, Y_j), представляющих полную группу событий, то сумма их вероятностей равна единице, т.е.

= 1

Итоговые строки или столбцы таблицы представляют собой законы распределения соответствующих одномерных случайных величин.

Действительно, распределение одномерной случайной величины Х можно получить, вычислив вероятности событий Х= X_i (_i = 1,2, …,n) как сумму вероятностей несовместных событий, рассматривая первый и последний столбцы таблиц в качестве закона распределения:

P_i = Р(Х= X_i) = Р[(Х= X_i)(У=У₁)+…+(Х= X_i)(У=Y_j)+…+ (Х= X_i)(У= Y_m)] =

= P_i1 + …+ P_ij +…+ P_im = .