4.Інтерполяційна формула Ньютона

Інтерполяційні формули Ньютона — формули обчислювальної математики, що застосовуються для поліноміальної інтерполяції.

Якщо вузли інтерполяції рівновіддалені та впорядковані, так що , то існує   , тобто  інтерполяційний многочлен можна записати в формі Ньютона.

Інтерполяційні поліноми в формі Ньютона зручно використовувати, коли точка интерполяції знаходиться поблизу початку (пряма формула Ньютона) чи кінця таблиці (обернена формула Ньютона)

Коротка форма інтерполяційної формули Ньютона

У випадку рівновіддалених центрів інтерполяції, що знаходяться на однаковій відстані одне від одного, справедлива формула:

де   — біноміальні коефіцієнти, що належать області дійсних чисел..

Пряма інтерполяційна формула Ньютона

Так звана перша інтерполяційна формула Ньютона, що використовується для інтерполювання вперед

 де  , а вирази виду   — скінченні різниці.

Обернена інтерполяційна формула Ньютона

Так звана друга інтерполяційна формула Ньютона, що використовується для інтерполювання назад

 де  .

5.Інтерполяцій́ний поліном Лагра́нжа

Інтерполяцій́ний многочле́н Лагра́нжа — многочлен мінімального степеня, що приймає дані значення у даному наборі точок. Для   пар чисел  , де всі   різні, існує єдиний многочлен   степеня не більшого від  , для якого  .

У найпростішому випадку   - це лінійний многочлен, графік якого — пряма, що проходить через дві задані точки.

Визначення

Лагранж запропонував спосіб обчислення таких многочленів:

де базисні поліноми визначаються за формулою:

Очевидно, що   мають такі властивості:

• Це поліноми степеня 

• 

•  при 

Звідси випливає, що  , як лінійна комбінація  , може мати степінь не більший від  , та  .

Застосування

Поліноми Лагранжа використовуються для інтерполяції, а також для чисельного інтегрування.

Нехай для функції   відомі значення   у деяких точках. Тоді ця функція може інтерполюватися як

Зокрема,

Значення інтегралів від   не залежать від  , тож їх можна обчислювати заздалегідь, знаючи послідовність  .

Для випадку рівномірного розподілу на відрізку вузлів інтерполяції

У вказаному випадку можна виразити   через відстань між вузлами інтерполяції h та початкову точку  :

, і, як наслідок,

Якщо підставити ці вирази у формулу базисного полінома та винести h за знаки множення у чисельнику та знаменнику, отримаємо

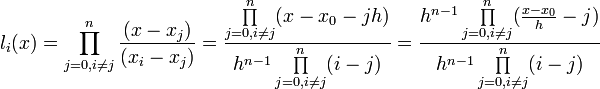
Після цього можна ввести заміну змінної і отримати поліном від у, який будується з використанням лише цілочисленної арифметики. Недоліком цього підходу є факторіальна складність чисельника та знаменника, що вимагає використання алгоритмів з багатобайтним представленням чисел.

Рис.3. Інтерполяційний многочлен Лагранжа для чотирьох точок 

6.Сплайн-функція

Сплайн (англ. spline — планка, рейка) — функція, область визначення якої розбита на куски, на кожному з кусків функція є деяким поліномом (многочленом).

В задачах інтерполяції, інтерполяція сплайном краща, ніж інтерполяція многочленом, оскільки дає схожі результати навіть при менших степенях поліномів, а також при її використанні не виникає феномена Рунге.

Максимальний степінь поліномів в сплайні називається степенем сплайна. Різниця між степенем сплайна і його гладкістю називається дефектом сплайна.

Означення та історія

Сплайн (spiline) називали гнучку металеву лінійку — універсальне лекало, що використовували креслярі для того, щоб гладко з'єднати окремі точки на кресленні. Тобто для графічного виконання інтерполяції. Більше того, крива, що описує деформацію гнучкої лінійки зафіксованої в окремих точках є сплайном. Отже, ми маємо фізичну модель сплайн-функції (або навпаки сплайн-функція є математичною моделлю гнучкої лінійки). Інтуїтивний підхід до використання кусочних функцій в задачах апроксимації зустрічався в математиці протягом тривалого часу. Але, як зазначає Корнейчук Н. П., вторгнення сплайнів в теорію наближення відбулося через задачі інтерполяції, завдяки їхнім хорошим обчислювальним та апроксимативним властивостям.

Початок розвитку теорії інтерполяції сплайнами та й сам термін сплайн відраховують з 1946 року зі статті Ізо Шонберга (Isaac Jacob Schoenberg). Особливо інтенсивний її розвиток відбувся в 50-70 роки, традиційною прикладною сферою використання інтерполяційних сплайнів стали в цей час системи автоматизованого проектування. Однак потенційні можливості сплайнів значно ширші ніж просто опис деяких кривих. В реальному світі велика кількість фізичних процесів за самою своєю природою є сплайнами. В механіці це деформація гнучкої пластини чи стержня, зафіксованих в окремих точках; траєкторія руху тіла, якщо сила, що діє на нього змінюється ступінчато (траєкторія штучного космічного об'єкта з активними та інерційними відрізками руху, траєкторія руху літака при ступінчатій зміні тяги двигунів та зміні профілю крила і т. д.). В термодинаміці це теплообмін в стержні складеному з фрагментів з різною теплопередачою. В хімії — дифузія через шари різних речовин. В електриці — поширення електромагнітних полів через різнорідні середовища. Тобто сплайн не надумана математична абстракція, а в багатьох випадках він є розв'язанням диференційних рівнянь, які описують цілком реальні фізичні процеси.

Розгляд сплайнів почнемо з визначення алгебраїчного сплайна [ ]: Функція   визначена і неперервна на відрізку   називається поліноміальним сплайном порядку  з вузлами  , якщо на кожному з відрізків  ,   є алгебраїчним поліномом степені, що не перевищує  , а в кожній з точок   деяка похідна   може мати розрив. Якщо в точці   неперервні функції  , а похідна   в точці   терпить розрив, число   називають дефектом сплайна. Множину   називають сіткою вузлів сплайна, а точки   вузлами або точками стикання чи склейки сплайна.

Як слідує з визначення, для побудови сплайна, що складається з   фрагмента потрібно знайти такі значення числових параметрів для кожного фрагмента — полінома степені  , які забезпечать неперервність у вузлах, як самої функції так і необхідних похідних. Отже всього слід визначити   параметрів. З врахуванням умови інтерполяції та неперервності перших двох похідних визначення параметрів зводиться до розв'язання системи з   лінійних рівнянь. Як правило, значення коефіцієнтів для відрізків поліномів безпосередньо не розраховуються.

Для визначення інтерполяційного сплайна з неперервною першою похідною достатньо розрахувати значення першої похідної у вузлах. Спосіб визначення похідних у вузлах сплайна визначає широку різноманітність інтерполяційних сплайнів. Часто похідні визначаються не як константи, а як деякі залежності від інтерпольованої функції та сітки інтерполяції.

Якщо значення першої похідної у вузлах розраховувати виходячи з умови неперервності другої похідної (вирішуючи систему з n лінійних рівнянь) то сплайн матиме дві неперервні похідні. Такий спосіб побудови сплайна, як і сам сплайн називають глобальним, оскільки при визначенні кожного з його коефіцієнтів враховується вся множина вузлів інтерполяції.

В інших випадках, для визначення окремого коефіцієнта, враховуються лише найближчі вузли інтерполяції і такі способи побудови, як і самі сплайни, називають локальними. Параметри фрагмента такого сплайна можна визначити незалежно від інших фрагментів.

Найпростішою умовою побудови фрагмента локального сплайна є умова рівності полінома на кінцях відрізків відповідним значенням інтерпольованої функції.

Для найпростішого сплайна — ламаної цієї умови цілком досить. Два коефіцієнта прямої однозначно визначаються з двох рівнянь. Такий сплайн є локальним. Для поліномів вищих степенів ми повинні додати додаткові умови таким чином, щоб загальне число рівнянь дорівнювало числу коефіцієнтів полінома. Так для сплайна 3-й степені такою умовою є рівність 1-ї похідної на кінцях відрізка деякому значенню, що визначається для сусідніх відрізків однаковим чином (у формулах (2) через значення похідної функції яку наближують).

Система з 4-х рівнянь

дозволяє однозначно визначити 4 коефіцієнти полінома. Для полінома 5-ї степені ми повинні додатково накласти умову рівності 2-ї похідної на кінцях відрізка і т. д. Наведене вище показує, чому сплайн будують переважно з поліномів непарних степенів (з парною кількістю коефіцієнтів).

Для поліномів парних степенів при складанні системи (3) залишається невизначеною похідна в одному з кінців відрізка і умова рівності похідних (гладкості кривої) не виконуватиметься. Тому для полінома 2-ї степені неможливо досягти рівності першої похідної в точках стику, а для 4-ї степені другої похідної і так далі, виходячи з системи рівнянь (3). Для побудови сплайнів з парними степенями штучно додають додаткові умови щоб сформувати систему рівнянь подібну (3). Коли похідні полінома сплайна визначаються як відповідні похідні інтерпольованої функції, то сплайн є ермітовим.

Існують локальні методи побудови сплайнів Бесселя та Акіми, B — сплайни [] . В основному коли йде мова про сплайни то мають на увазі сплайни побудовані з алгебраїчних поліномів. Саме таких до них відноситься приведене вище визначення. Саме ці сплайни є найбільше вивченими. Проте сплайн може складатися з фрагментів функцій будь-якого класу. В [] розглянуто побудову таких сплайнів, та досліджуються їхні властивості. Автор не дає загального визначення побудованих сплайнів. Очевидно, що для довільних класів функцій з яких складається сплайн наведене на початку статті визначення не зовсім годиться. Якщо, наприклад, сплайн складається з відрізків експоненти то поняття дефекту сплайна втрачає зміст. Хоча кількість неперервних похідних залишиться важливою характеристикою. Побудова сплайна, фрагментами якого є розривні функції (раціональні функції, функції Паде) дещо виходить за рамки сплайнової ідеї, оскільки однією з основних переваг сплайнів є їхня гладкість. Якщо довільно розширювати такі конструкції, то стираються відмінності сплайнів від кускових функцій. Іншою перевагою сплайнів є ефективність обчислень. Надмірне ускладнення фрагментів суттєво знижує переваги сплайнів перед класичними функціями.

Для сплайнів є характерними такі ознаки: сплайн складається з фрагментів — функцій одного класу, які різняться лише своїми параметрами; на сусідні фрагменти в точках стикування накладаються певні умови, що зводяться до неперервності значень та деяких перших похідних. Сплайни — напрямок прикладної математики, що інтенсивно розвивається.

Форма представлення. Функції, що задають фрагменти сплайна, як правило, залежать від множини параметрів, завдяки яким вони змінюють свою форму. Значення параметрів на кожному із фрагментів індивідуальні. Ці параметри можуть задавати конкретний сплайн. Для поліноміальних сплайнів це поліноміальні коефіцієнти. Отже, сплайн можна представити множиною параметрів функцій на кожному з фрагментів. Назвемо це представлення пофрагментним. Таке представлення є наглядним, часто має явний фізичний зміст. Але число параметрів є надмірним. Так, для кубічного сплайна необхідно мати 4*(r-1) параметри (r — число вузлів сплайна). Значно компактнішим є представлення сплайна у вигляді полінома, через базисні сплайн-функції у вигляді:

,

де   — базисні сплайн-функції (як правило локальні),   — числові коефіцієнти, що задають вагу базисних функцій при формуванні сплайна. Число параметрів, що задають сплайн рівне числу вузлів сплайна. Між параметрами функції на фрагменті та коефіцієнтами полінома-сплайна існує залежність, що дозволяє за одними коефіцієнтами знаходити інші, хоча формули можуть мати досить складний вигляд.

6.1 B-сплайн

B-сплайн (базисний сплайн) — сплайн-функція, що має мінімальний носій для заданого степеня, гладкості та області визначення.

Фундаментальна теорема стверджує, що довільна сплайн-функція заданого степеня, гладкості і області визначення може бути представлена як лінійна комбінація B-сплайнів того ж степеня і гладкості на тій же області визначення.

Термін B-сплайн запровадив Ісак Яков Шонберг в 1947 році.

Визначення

B-сплайн степеня n з заданими вузлами:

та (m−n) контрольними точками

Це параметрична крива задана на   що складена з базисних B-сплайнів степеня n

Базисні B-сплайни визначаються рекурсивними формулами:

 при 

При одинаковій відстані між сусідніми вузлами B-сплайни називаються однорідними, в протилежному випадку — неоднорідними.

Однорідні B-сплайни

Для однорідних B-сплайнів, базисні B-сплайни одинакового степеня є зміщеними екземплярами однієї функції. Нерекурсивним визначенням базисних B-сплайнів є

де

Приклади

Константні B-сплайни

Це найпростіші сплайни. Вони не є навіть неперервними.

Лінійні B-spline

Лінійні B-сплайни є неперервними, але не диференційовними.

Однорідні квадратичні B-сплайни

Є найбільш вживаною формою B-сплайнів.

В матричній формі:

Однорідні кубічні B-сплайни